Binomial conjugado como é resolvido, exemplos, exercícios

A Binomial conjugado De outro binomial é aquele em que eles diferem apenas por um sinal da operação. O binomial, como o nome indica, é uma estrutura algébrica que consiste em dois termos.

Alguns exemplos de binômios são: (A + b), (3m - n) e (5x - y). E seus respectivos binômios conjugados são: (a - b), (-3m - n) e (5x + y). Como pode ser visto imediatamente, a diferença está no sinal.

figura 1. Um binomial e seu binomial conjugado. Eles têm os mesmos termos, mas diferem no sinal. Fonte: f. Zapata.

Um binomial multiplicado por seu conjugado resulta em um produto notável que é usado muito em álgebra e ciência. O resultado da multiplicação é a subtração dos quadrados dos termos do binomial original.

Por exemplo, (X - y) É um binomial e seu conjugado é (x + y). Então, o produto dos dois binômios é a diferença dos quadrados dos termos:

(X - y).(x + y) = x² - e²

[TOC]

Como um binomial conjugado é resolvido?

A regra enunciada aos binômios conjugados é a seguinte: 

O produto de dois binômios conjugados é igual ao quadrado do primeiro termo menos o quadrado do segundo termo. Este resultado é chamado de diferença quadrada.

Como exemplo de aplicação, começaremos demonstrando o resultado anterior, o que pode ser feito usando a propriedade distributiva do produto em relação à soma algébrica.

(x - y) (x + y) = x.x + x.e e.X - y.e

A multiplicação anterior foi obtida após estas etapas:

- O primeiro mandato do primeiro binomial é multiplicado pelo primeiro mandato do segundo

- Então o primeiro dos primeiros, para o segundo dos segundo

- Então o segundo dos primeiros para o primeiro dos segundo 

- Finalmente o segundo dos primeiros para o segundo dos segundo.

Pode servir você: álgebra vetorial

Agora vamos fazer uma pequena mudança usando propriedades comutativas: e.x = x.e. Permanece assim:

(x - y) (x + y) = x.x + x.y - x.e e.e

Como existem dois termos iguais, mas de outra forma (destacados em cores e sublinhados), eles são cancelados e simplificados:

(x - y) (x + y) = x.X - y.e

Finalmente, é aplicado que multiplicar um número por si só é equivalente a levantá -lo quadrado, então x.x = x² e também e.y = y².

Dessa maneira, o que havia sido apontado na seção anterior, que o produto de uma soma para sua diferença é a diferença dos quadrados:

(X - y).(x + y) = x² - e²

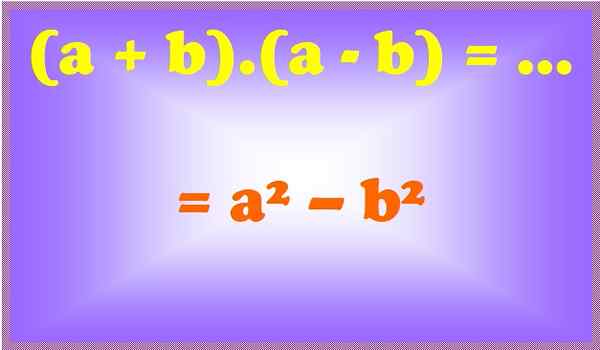Figura 2. Uma soma para sua diferença é uma diferença de quadrados. Fonte: f. Zapata.

Exemplos

- Binômios conjugados de várias expressões

Exemplo 1

Encontre o conjugado de (e² - 3y).

Responder: (e² + 3y)

Exemplo 2

Obtenha o produto de (e² - 3y) por seu conjugado.

Responder: (e² - 3y) (e² + 3y) = (e²)² - (3y)² = y⁴ - 3² e² = y⁴ - 9y²

Exemplo 3

Desenvolva o produto (1 + 2a).(2a -1).

Responder: A expressão anterior é equivalente a (2a + 1).(2a -1), isto é, corresponde ao produto de um binomial para seu conjugado.

Sabe -se que o produto de um binomial para seu binomial conjugado é igual à diferença dos quadrados dos termos binomiais:

(2a + 1) (2a -1) = (2a)² - 1² = 4 a² - 1

Exemplo 4

Escreva o produto (x + y + z) (x - y - z) como uma diferença de quadrados.

Responder: Podemos assimilar os trinômios antes da forma de binômios conjugados, fazendo uso cuidadoso de parênteses e colchetes:

(x + y + z) (x - y - z) = [x + (y + z)] [x - (y + z)]

Dessa maneira, a diferença de quadrados pode ser aplicada:

(x + y + z) (x - y - z) = [x + (y + z)].[x - (y+z)] = x² - (Y+z)²

Exemplo 5

Expressar o produto (M² - m -1).(m² + m -1) como uma diferença em quadrados.

Pode atendê -lo: 120 divisores

Responder: A expressão anterior é o produto de dois trinômios. Primeiro, deve ser reescrito como o produto de dois binômios conjugados:

(m² - M -1) (M² + m -1) = (M² - 1 - m) (M² -1 + m) = [(M² -1) - M].[(m² -1) +m)]

Aplicamos o fato de que o produto de um binomial por seu conjugado é a diferença quadrática de seus termos, conforme explicado:

[(m² -1) - M].[(m² -1) +m)] = (M² -1)² - m²

Exercícios

Como sempre, começa com os exercícios mais simples e o nível de complexidade está aumentando.

- Exercício 1

Escripa (9 - A²) como um produto.

Solução

Primeiro, reescrevemos a expressão como uma diferença de quadrados, a fim de aplicar o que explicou anteriormente. Portanto:

(9 - A²) = (3² - para²)

Remacemos imediatamente, o que é equivalente a escrever essa diferença de quadrados como um produto, conforme solicitado na declaração:

(9 - A²) = (3² - para²) = (3 + a) (3 -a)

- Exercício 2

Fature 16x² - 9y⁴.

Solução

Fator Uma expressão significa escrevê -lo como um produto. Nesse caso, é necessário reescrever anteriormente a expressão, para obter uma diferença de quadrados.

Não é difícil fazê -lo, pois observando cuidadosamente, todos os fatores são quadrados perfeitos. Por exemplo 16 é o quadrado de 4, 9 é o quadrado de 3, e⁴ é o quadrado de e² e x² é o quadrado de X:

16x² - 9y⁴  = 4²x² - 3²e⁴ = 4²x²  - 3²(e²)²

Então o que já sabemos é aplicado: que uma diferença nos quadrados é o produto de binômios conjugados:

(4x)² - (3 e²)² = (4x - 3 e²) . (4x + 3 e²)

- Exercício 3

Escreva (a - b) como um produto binomial

Solução

A diferença anterior deve ser escrita como diferenças quadradas

(√a)² -(√b)²

Em seguida, é aplicado que a diferença nos quadrados é o produto dos binômios conjugados

Pode atendê -lo: redução de termos semelhantes

(√a - √b) (√a + √b)

- Exercício 4

Um dos usos do binomial conjugado é a racionalização de expressões algébricas. Este procedimento consiste em eliminar as raízes do denominador de uma expressão fracionária, que em inúmeras ocasiões facilita as operações. É solicitado a usar o binomial conjugado para racionalizar a seguinte expressão:

√ (2 -x) / [√3 - √ (2+x)]]

Solução

O primeiro é identificar o binomial conjugado do denominador: [√3 + √ (2 + x)]].

Agora, multiplicamos o numerador e o denominador da expressão original pelo binomial conjugado:

√ (2 -x) [√3+√ (2+x)] /[√3 - √ (2+x)].[√3 + √ (2 + x)]

No denominador da expressão anterior, reconhecemos o produto de uma diferença por uma soma, que já sabemos que corresponde à diferença dos quadrados dos binômios:

√ (2-x) .[√3 + √ (2 + x)] /(√3)² - [√ (2+x)]² 

Simplificar o denominador é:

√ (2-x).[√3+√ (2+x)] / [3 - (2+x)] = √ (2 -x). [√3 + √ (2 + x)] / (1 - x)

Agora, cuidamos do numerador, pelo qual aplicaremos a propriedade distributiva do produto em relação à soma:

√ (2-x) .[√3 + √ (2 + x)] / (1 - x) = √ (6-3x) + √ [(2 -x) (2 + x)] / (1 - x)

Na expressão anterior, reconhecemos o produto do binomial (2-x) para seu conjugado, que é o produto notável igual à diferença de quadrados. Dessa maneira, uma expressão racionalizada e simplificada é finalmente obtida:

[√ (6-3x) + √ (4-x²)] / (1 - x)

- Exercício 5

Desenvolva o seguinte produto, usando as propriedades do binomial conjugado:

[2º^{(x + 3y)} - 3º^{(x - 3y)}].[2º^{(x + 3y)} + 3º^{(x - 3y)}]

Solução

4º^{(2x + 6y)} - 9º^{(2x - 6y)} = 4a^(2x) .para^(6y) - 9º^(2x) .para^(-6y)= [4a^(6y) - 9º^(-6y)] .para^(2x)

O leitor atencioso terá notado o fator comum que foi destacado na cor.

Referências

1. Baldor, a. 1991. Álgebra. Editorial cultural venezuelano.PARA.
2. González J. Exercícios binomiais conjugados. Recuperado de: Academia.Edu.
3. Matemática Alex. Produtos notáveis. Recuperado do YouTube.com.
4. Math2me. Binômios conjugados/ produtos notáveis. Recuperado do YouTube.com.
5. Produtos binomiais conjugados. Recuperado de: LMS.Colbachenlinea.mx.
6. Vitual. Binômios conjugados. Recuperado de: youtube.com.