Definição da plataforma fatorial, fórmulas e exercícios

Ele Plataforma fatorial É uma máquina simples que consiste em um arranjo de polia com um efeito multiplicador da força. Dessa forma, você pode aumentar uma carga aplicando apenas o equivalente a uma fração do peso na extremidade livre da corda.

Consiste em dois conjuntos de polias: uma que é fixada a um suporte e outro que exerce a força resultante na carga. As polias são montadas em uma estrutura geralmente metálica que as segura. 

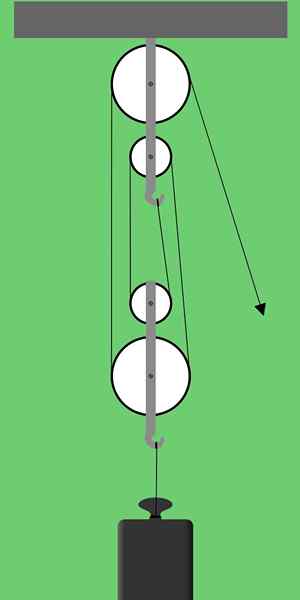
figura 1. Esquema de uma plataforma fatorial. Fonte: Pixabay

A Figura 1 mostra uma plataforma fatorial que consiste em dois grupos de duas polias cada. Este tipo de arranjo de polia também é chamado Rig qualquer Polypasts.

[TOC]

Fórmulas Fatoriais da direita

Caso 1: uma polia móvel e um fixo

Para entender por que esse arranjo multiplica a força exercida, começaremos com o caso mais simples, consistindo de uma polia fixa e móvel.

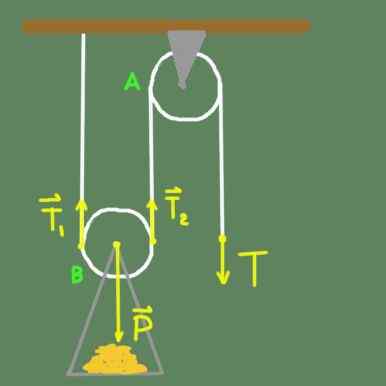Figura 2. Duas Polia.

Na Figura 2, temos uma polia fixa no telhado por suporte. A polia a pode girar livremente em torno de seu eixo. Também temos uma polia B que tem um suporte fixo ao eixo da polia, no qual a carga é colocada. A polia B, além de poder girar livremente em torno de seu eixo, tem a possibilidade de se mover verticalmente.

Suponha que estamos em uma situação de equilíbrio. Considere as forças que atuam na polia B. O eixo B -Pulley suporta um peso total P que é direcionado para baixo. Se essa era a única força na polia B, então, mas sabemos que a corda que passa por esta polia também exerce duas forças, que são os T1 e T2 que são direcionados para cima.

Para que o equilíbrio translacional, as duas forças devem ser as mesmas com o peso que suporta o eixo da polia B.

T1 + T2 = P

Mas como a polia B também está em equilíbrio rotacional, então T1 = T2. As forças T1 e T2 vêm da tensão aplicada à corda, chamada T.

Pode atendê -lo: Bohr Atomic Model

Portanto t1 = t2 = t. Substituir na equação anterior permanece:

T + T = P

2t = p

Indicando que a tensão aplicada à corda é apenas metade do peso:

T = P/2

Por exemplo, se a carga fosse 100 kg, seria suficiente para aplicar uma força de 50 kg na extremidade livre da corda para aumentar a carga em velocidade constante.

Caso 2: duas polias móveis e duas fixo

Vamos considerar as tensões e forças que agem em um conjunto que consiste em dois suportes de suportes A e B com duas polias cada.

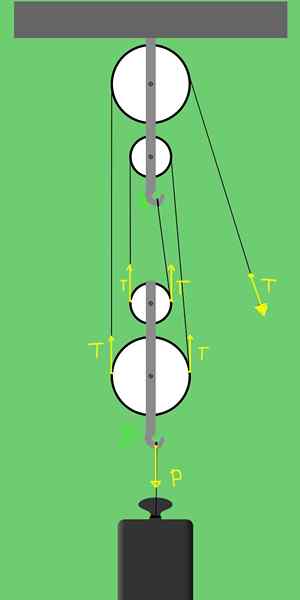Figura 3. Forças em uma plataforma de 2 polias fixas e 2 polias móveis.

O suporte B tem a possibilidade de se mover verticalmente, e as forças que atuam no filho:

- O peso P da carga, que aponta verticalmente para baixo.

- Duas tensões na grande polia e duas tensões na pequena polia. No total, quatro tensões, todas apoiando.

Para que haja equilíbrio de tradução, é necessário que as forças que apontam verticalmente para cima igual à carga que aponta para baixo. Isto é, deve ser cumprido:

T + t + t + t = p

Isto é, 4 t = p

De onde se segue que a força aplicada t na extremidade livre da corda é apenas um quarto do peso devido à carga que deseja subir., T = P / 4.

Com esse valor para tensão T, a carga pode ser mantida estática ou subindo com velocidade constante. Se uma tensão maior fosse aplicada do que esse valor, a carga aceleraria, uma condição necessária para removê -la do resto.

Caso geral: n polias móveis e n polias fixas

Como visto nos casos anteriores, para cada polia do conjunto móvel, existem algumas forças para cima pela corda que passa pela polia. Mas essa força não pode ser nada além da tensão aplicada à corda na extremidade livre.

Então, para cada polia de conjunto móvel, haverá uma força ascendente que vale 2T. Mas como existem N polias no conjunto móvel, é necessário apontar verticalmente para cima é:

Pode atendê -lo: mecanismo de gaiola de esquilo

2 n t

Para equilíbrio vertical, é necessário que:

2 n t = p

Portanto, a força aplicada na extremidade livre é:

T = p / (2 n)

Nesse caso, pode -se dizer que a força exercida t multiplica 2 n vezes na carga.

Por exemplo, se tivéssemos uma plataforma fatorial de 3 polias fixas e 3 celulares, o número n seria igual a 3. Por outro lado, se a carga fosse p = 120 kg, a força aplicada na extremidade livre seria t = 120 kg / (2*3) = 20 kg.

Exercícios resolvidos

Exercício 1

Considere uma plataforma fatorial composta por duas polias fixas e duas polias móveis. A tensão máxima que pode suportar a corda é de 60 kg. Determine qual é a carga máxima que pode ser colocada.

Solução

Quando a carga está em repouso ou movendo -se constantemente o peso P, está relacionada à tensão t aplicada na corda por meio do seguinte relacionamento:

P = 2 n t

Como é uma plataforma de dois celulares e duas polias fixas, então n = 2.

A carga máxima que pode ser colocada é obtida quando t tem o valor máximo possível, que neste caso é de 60 kg.

Carga máxima = 2*2*60 kg = 240 kg

Exercício 2

Encontre a relação entre a tensão da corda e o peso da carga, em uma plataforma fatorial de duas polias nas quais a carga acelera com aceleração para.

Solução

A diferença neste exemplo em relação ao que foi visto até agora é que a dinâmica do sistema deve ser considerada. Então, propomos a segunda lei de Newton para encontrar o relacionamento solicitado.

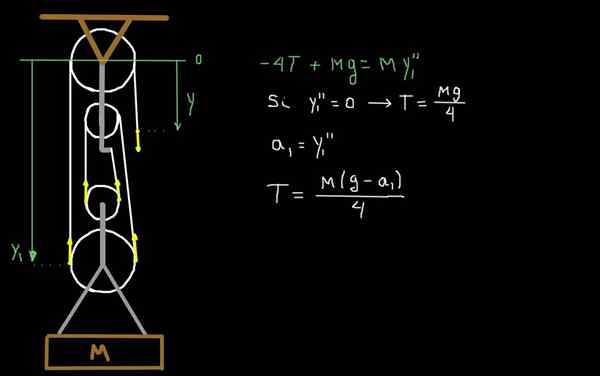Figura 4. Dinâmica da plataforma fatorial.

Na Figura 4, desenhamos as forças devido à tensão t da corda. A parte móvel da plataforma tem uma massa total m. Tomamos como sistema de referência um no nível da primeira polia fixa e positiva.

Y1 é a posição mais baixa do eixo da polia.

Aplicamos a segunda lei de Newton para determinar a aceleração A1 da parte móvel da plataforma:

Pode atendê -lo: teorema de varignon

-4 t + mg = m a1

Como o peso da carga é p = mg, onde g é a aceleração da gravidade, o relacionamento anterior pode ser escrito:

-4t + p = p (a1 / g)

Se quiséssemos determinar a tensão aplicada na corda quando uma certa carga de peso é acelerada com a aceleração A1, o relacionamento anterior seria assim:

T = p (1 - a1 / g) / 4

Observe que se o sistema estivesse em repouso ou se movendo constantemente, então A1 = 0, e recuperamos a mesma expressão que obtivemos no caso 2.

Exercício 3

Neste exemplo, é usado o mesmo equipamento do Exercício 1, com a mesma corda que suporta um máximo de 60 kg de tensão. Uma certa carga aumenta, acelerando -a de repouso para 1 m/s por 0,5 s, usando a tensão máxima da corda. Encontre o peso máximo de carga.

Solução

Usaremos as expressões obtidas no Exercício 2 e o sistema de referência na Figura 4, no qual o endereço positivo é vertical para baixo.

A aceleração da carga é A1 = (-1 m/s -0 m/s)/0,5 s = -2 m/s^2.

O peso da carga em quilograma é dado por

P = 4 t / (1 - a1 / g)

P = 4*60 kg / (1 + 2/9.8) = 199,3 kg

Este é o peso máximo possível da carga sem que a corda seja quebrada. Observe que o valor obtido é menor que o obtido no Exemplo 1, no qual a carga foi suposta com aceleração zero, isto é, em repouso ou velocidade constante.

Referências

1. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1. 101-120.
2. Resnick, r. (1999). Físico. Vol. 1. 3 ra ed. em espanhol. Empresa Editorial Continental S.PARA. claro.V. 87-103.
3. Giancoli, d. 2006. Física: Princípios com aplicações. 6º. Ed. Prentice Hall. 72 - 96.
4. Hewitt, Paul. 2012. Ciência física conceitual. 5 ª. Ed. Pearson.38-61.
5. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7º. Ed. Cengage Learning. 100 - 119.