Características de amplitude das ondas, fórmulas e exercícios

O Amplitude de onda É o deslocamento máximo experimentado por um ponto em uma onda em relação à posição de equilíbrio. As ondas se manifestam em todos os lugares e muitas maneiras do mundo ao nosso redor: no oceano, no som e na corda de um instrumento que o produz, à luz, na superfície da terra e muito mais.

Uma maneira de produzir ondas e estudar seu comportamento é observar a vibração de uma corda que tem uma extremidade fixa. Ao produzir um distúrbio no outro extremo, cada partícula do corda oscila e, com ela, a energia da perturbação é transmitida na forma de uma sucessão de pulsos por toda parte.

As ondas se manifestam de várias maneiras na natureza. Fonte: Pixabay.

À medida que a energia se espalha, a corda que deveria ser perfeitamente elástica adota a forma sinusoidal típica com cumes e vales mostrados na figura que aparece abaixo na seção a seguir.

[TOC]

Características e significado de amplitude de onda

A amplitude A é a distância entre a crista e o eixo de referência ou nível 0. Se preferir, entre um vale e o eixo de referência. Se o distúrbio na corda é leve, a amplitude A é pequena. Se, pelo contrário, o distúrbio for intenso, a amplitude será maior.

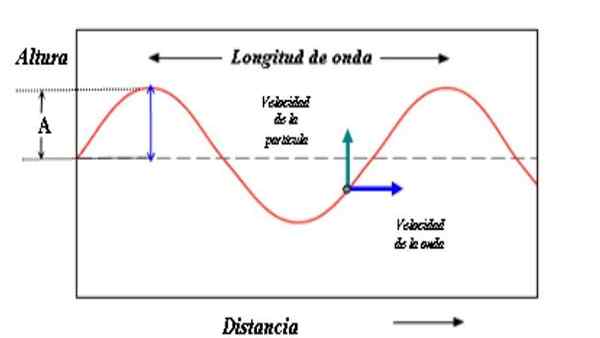Um modelo para descrever a onda consiste em uma curva sinusoidal. A amplitude das ondas é a distância entre uma crista ou vale e o eixo de referência. Fonte: PACO [CC BY-SA 3.0 (http: // criativecommons.Org/licenças/BY-SA/3.0/]]

O valor da amplitude também é uma medida da energia que usa a onda. É intuitivo que grande amplitude esteja associada a maiores energias.

De fato, a energia é proporcional ao quadrado da amplitude, que expressa matematicamente é:

Eu ∝a²

Pode atendê -lo: Indutância mútua: fórmula/coeficiente, aplicações, exercícios

Onde eu é a intensidade da onda, por sua vez relacionada à energia.

O tipo de onda produzida no exemplo de corda pertence à categoria de ondas mecânicas. Uma característica importante é que cada partícula na corda sempre permanece muito próxima de sua posição de equilíbrio.

As partículas não se movem ou se movem pela corda. Eles variam para cima e para baixo. Isso é indicado no esquema superior com a seta verde, no entanto, a onda junto com sua energia, viaja da esquerda para a direita (Blue Arrow).

Ondas que se espalham na água fornecem as evidências necessárias para se convencer disso. Observando o movimento de uma folha que caiu em uma lagoa, pode -se ver que ela simplesmente oscila que acompanha o movimento da água. Não vai muito longe, pelo menos claro, que existem outras forças que fornecem outros movimentos.

O modelo de onda mostrado na figura consiste em um padrão repetitivo no qual a distância entre duas cristas é o comprimento de onda λ. Se você quiser, o comprimento de onda também separa dois pontos idênticos da onda, mesmo quando eles não estão na crista.

A descrição matemática de uma onda

Naturalmente, a onda pode ser descrita por uma função matemática. Funções periódicas como seio e cosseno são o ideal para a tarefa, se você deseja representar a onda tanto no espaço quanto no tempo.

Se chamarmos o eixo vertical na figura e o eixo horizontal, chamamos de "t", o comportamento da onda ao longo do tempo é expresso por:

y = um cos (ωt + δ)

Para esse movimento ideal, cada partícula de corda oscila com movimento harmônico simples, que se origina graças a uma força que é diretamente proporcional ao deslocamento feito pela partícula.

Pode atendê -lo: Dirac Jordan Atomic Model: características e postulações

Na equação proposta, a, ω e δ são parâmetros que descrevem o movimento, sendo para o amplitude previamente definido como o deslocamento máximo experimentado pela partícula em relação ao eixo de referência.

O argumento do cosseno é chamado Fase de movimento E δ é o constante de fase, Qual é a fase quando t = 0. Tanto a função cosseno quanto a função seno.

Geralmente é possível escolher t = 0 com δ = 0 para simplificar a expressão, obtendo:

y = um cos (ωt)

Quando o movimento é repetitivo no espaço e no tempo, há um tempo característico que é o período t, definido como o tempo necessário para a partícula executar uma oscilação completa.

Descrição da onda no tempo: parâmetros característicos

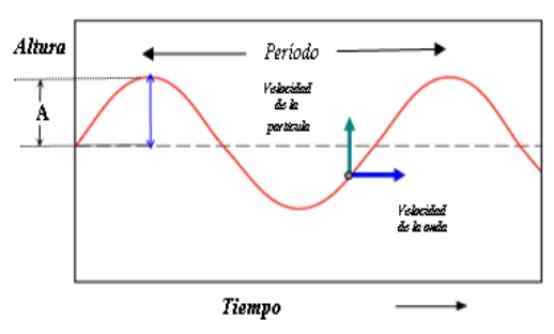Esta figura mostra a descrição da onda no tempo. A distância entre os cumes (ou vales) agora corresponde ao período de onda. Fonte: PACO [CC BY-SA 3.0 (http: // criativecommons.Org/licenças/BY-SA/3.0/]]

Agora, tanto a mama quanto o cosseno repetem seu valor quando a fase aumenta no valor 2π, de modo que:

ωt = 2π → ω = 2π /t

Ω é chamado Frequência angular de movimento E tem dimensões do inverso do tempo, sendo suas unidades no sistema internacional Radián / Segundo^-1.

Finalmente você pode definir o Frequência de movimento F, como o inverso ou recíproco do período. Representa no número de cristas por unidade de tempo, nesse caso:

F = 1/t

Ω = 2πf

Ambos F e ω têm as mesmas dimensões e unidades. Além do segundo^-1, que é chamado Hertz ou Hertzio, é comum ouvir sobre Revoluções por segundo qualquer revoluções por minuto.

Velocidade da onda v, que devem ser enfatizados de que não é o mesmo que o experimentado pelas partículas, pode ser facilmente calculado se o comprimento de onda λ e a frequência f forem conhecidos:

Pode servir a você: corpos luminosos: características e como elas geram sua própria luz

V = λf

Se a oscilação experimentada pelas partículas é do tipo simples de harmônico, a frequência angular e a frequência dependem apenas da natureza das partículas oscilantes e das características do sistema. A amplitude da onda não afeta esses parâmetros.

Por exemplo, ao tocar uma nota musical em um violão, a nota sempre terá o mesmo tom, embora seja tocada com maior ou menor intensidade, dessa maneira A fazer sempre soará como um, embora seja ouvido mais forte ou mais macio em uma composição, em um piano ou em um violão.

Na natureza, ondas que são transportadas em um ambiente material em todas as direções são atenuadas porque a energia se dissipa. Por esse motivo, a amplitude diminui com o inverso da distância r para a fonte, sendo possível afirmar que:

A∝1/r

Exercício resolvido

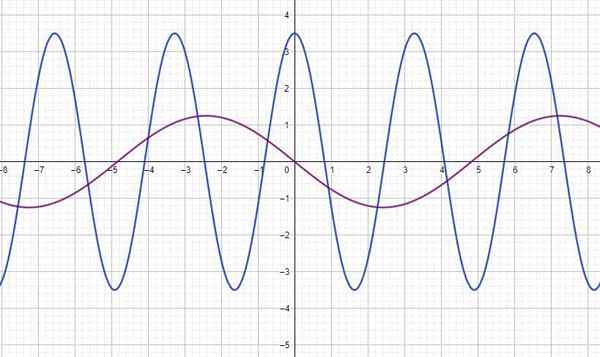
A figura mostra a função y (t) para duas ondas, onde e está em medidores e t em segundos. Para cada um encontro:

a) amplitude

b) período

c) Frequência

d) a equação de cada onda em termos de seios ou cosenos.

Respostas

a) É medido diretamente do gráfico, com a ajuda da grade: onda azul: a = 3.5m; Fuchsia Wave: A = 1.25 m

b) Ele também lê o gráfico, determinando a separação entre dois picos ou vales, consecutivos: Blue Wave: t = 3.3 segundos; Fuchsia Wave t = 9.7 segundos

c) É calculado lembrando que a frequência é o recíproco do período: Blue Wave: F = 0.302 Hz; Fuchsia Wave: F = 0.103 Hz.

d) onda azul: y (t) = 3.5 cos (ωt) = 3.5 cos (2πf.t) = 3.5 cos (1.9t) m; Fuchsia Wave: y (t) = 1.25 pecado (0.65T) = 1.25 cos (0.65T+1.57)

Observe que a onda fúcsia está desatualizada π/2 em relação ao azul, sendo possível representá -la com uma função seno. Ou cosseno deslocado π/2.