X quadrado

Explicamos o que é x quadrado, suas propriedades, exemplos e exercícios resolvidos

A área de um quadrado de "X" é x quadrado. Fonte: f. Zapata.

A operação algébrica de "X quadrado"É realizado multiplicando a quantidade" x "por si mesma duas vezes. Faz parte das operações de potenciação e, em símbolos matemáticos, é expresso desta maneira:

x ∙ x = x²

Este é um caso particular de empoderamento, no qual "x" representa o base E o "2" é o expoente. Se em uma operação, o termo x aparecer², Ele lê precisamente como "x quadrado" ou "x quadrado elevado".

Naturalmente, outros expoentes são possíveis, por exemplo, se o expoente for 3, o poder é escrito como:

x ∙ x ∙ x = x³

E leia como "x para os três", "x criado para o cubo" ou simplesmente "x para o cubo".

Em geral, o expoente ao qual a base é alta pode ser qualquer número, chamado "n" e, nesse caso, o poder correspondente é escrito:

xⁿ = x ∙ x ∙ x ∙… ∙ x x

Aqui os pontos suspeitos indicam que "x" deve ser multiplicado por si mesmo "n", ou seja, quantas vezes o expoente indica.

Alguns exemplos simples de "x quadrado", com números, são os seguintes:

3² = 3 ∙ 3 = 9

(-4)² = (−4) ∙ (−4) = 16

Posterior, várias aplicações são descritas para as quais é necessário.

Propriedades da potencialização

Em geral, o produto de qualquer quantidade consigo mesmo, n vezes, é chamado de potencialização. O cálculo do X ao quadrado é apenas um caso particular de potenciação, dois outros casos aparecem quando você deseja aumentar um valor para o expoente 1, obtendo como resultado a mesma quantidade:

Pode atendê -lo: leis de expoentes

Como essas operações são frequentes, para trabalhar com bases e expoentes, algumas regras operacionais simples são seguidas, chamadas Leis dos expoentes, que estão listados abaixo:

Leis dos expoentes

A seguir, "X" é a base e "n" e "m" são os expoentes.

1.- Produto de poderes básicos iguais

Ao multiplicar dois (ou mais) poderes de base igual, é obtida a base elevada à soma dos expoentes:

xⁿ∙ x^m = x^n+m

No caso de x alto, esta regra é aplicada da seguinte maneira, substituindo N e M por 1:

x¹∙ x¹ = x¹⁺¹ = x²

2.- Divisão de Powers de Base Igual

Ao dividir os poderes da mesma base, a base é obtida, elevada à subtração entre os respectivos expoentes do numerador e o denominador:

xⁿ ÷ x^m = x^N-m

Como a divisão por 0 não é definida, deve ser cumprido, desde que x ≠ 0.

3.- Poder de um poder

O resultado do poder de um poder é igual à base elevada ao produto dos expoentes:

(x^m)ⁿ = x^m∙n

Pode ser obtido novamente x quadrado, ao fazer m = 1 e n = 2:

(x¹)² = x^1∙2 = x²

4.- Expoente negativo

Para expoentes negativos, a operação a ser realizada é:

Sempre que x ≠ 0. Observe que, neste caso, o poder se torna uma fração com um numerador igual a 1.

5.- Expoente fracionário

Os expoentes fracionários podem ser escritos como a enésima raiz da base:

Sob condição de que n é diferente de 0. Esse valor se torna o índice raiz, enquanto M se torna o expoente da quantidade sob a raiz, que neste caso é x.

Pode atendê -lo: qual é a diretriz? (Geometria)

Produtos e quocientes de bases diferentes

Quando você precisa aprimorar produtos e quocientes de diferentes bases "X" e "Y", essas regras são seguidas:

1.- Poder do produto

Para executar esse poder, cada quantidade é aumentada para o expoente n e o produto resultante é estabelecido:

(x ∙ y)ⁿ = xⁿ ⋅ eⁿ

2.- Proporção do quociente

Novamente, cada quantidade deve ser aumentada ao expoente n separadamente e estabelecer o quociente que resulta, após a regra de que a quantidade “y” é diferente de 0, no caso de “n” positivo:

(x ÷ y)ⁿ = xⁿ ÷ yⁿ

Quando "n" é negativo, deve ser tomado cautela, por causa da propriedade 4 da seção anterior, o numerador se torna um denominador. Nesse caso, ambas as quantidades devem ser diferentes de 0, uma vez que a divisão em 0 deve ser evitada a todo custo.

Exemplos

Exemplo 1: quadrados de números naturais

Os quadrados dos dez primeiros números naturais são:

• 1²= 1 × 1 = 1
• 2²= 2 × 2 = 4
• 3²= 3 × 3 = 9
• 4²= 4 × 4 = 16
• 5²= 5 × 5 = 25
• 6²= 6 × 6 = 36
• 7²= 7 × 7 = 49
• 8²= 8 × 8 = 64
• 9²= 9 × 9 = 81
• 10²= 10 × 10 = 100

Exemplo 2: O quadrado de números negativos

O quadrado de um número negativo é sempre positivo, uma vez que duas quantidades de sinal igual são multiplicadas, portanto:

(-x) · (-x) = x ∙ x = x²

Por exemplo:

(-2) · (-2) = (-2)² = 4

Exemplo 3: quadrado da soma e diferença

Muitas vezes, é necessário calcular o quadrado da soma de duas quantidades, ou sua diferença, operações incluídas na categoria de produtos notáveis.

A operação é resolvida com as indicações dadas e a ajuda de propriedades distributivas:

Quadrado da soma

Deixe duas quantidades "x" e "y", e você deseja encontrar o quadrado de sua soma (x + y)²:

Pode atendê -lo: hierarquia de operações

(x + y)² = (x + y) ∙ (x + y) = x ∙ x + x ∙ y + y ∙ x + y ∙ y = x² + 2x ∙ y + e²

Esta expressão é assim: "quadrado do primeiro, além do duplo produto do primeiro para o segundo mais o quadrado do segundo".

Quadrado de diferença

É resolvido de forma análoga, mas levando em consideração o sinal negativo:

(x - y)² = (x - y) ∙ (x - y) = x ∙ x - x ∙ y + y ∙ x - y ∙ y = x² - 2x ∙ e + e²

Exemplo 4: A área de um quadrado

O quadrado é um polígono de 4 anos, que tem a mesma medida. Seja ℓ a medição lateral, então a área A da figura é dada por:

A = ℓ²

Exemplo 5: Teorema de Pitágoras

Este teorema se aplica aos triângulos retângulo, aqueles em que dois de seus lados formam ângulo reto. Esses lados são conhecidos como "categorias" e o lado restante é o "hipotenusa".

O teorema estabelece que o quadrado do hipotenusa é igual à soma dos quadrados das categorias. Chamando "A" e "B" para as categorias e "C" para a hipotenusa, o teorema é escrito como:

c² = a² + b²

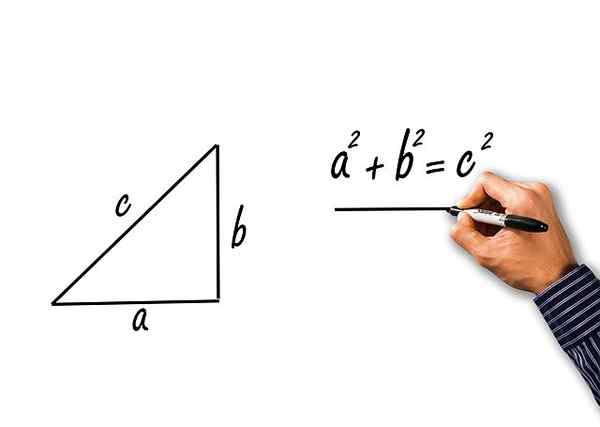Teorema de Pitágoras para um triângulo retângulo de gatos A e B, e hipotenusa c

Exercícios resolvidos

Exercício 1

Calcule o quadrado da hipotenusa cujas pernas medem 3 e 5 unidades.

Solução

De acordo com o teorema de Pitágoras, o quadrado da hipotenusa é:

c² = a² + b²

Substituindo os valores:

c² = 3² + 5²= (3 × 3) + (5 × 5) = 9 + 25 = 34

Exercício 2

Determine a área de um quadrado lateral ℓ = 6 cm

Solução

A = ℓ² = (6 cm)² = 36 cm²