Definição de velocidade instantânea, fórmula, cálculo e exercícios

O velocidade instantânea É definido como a mudança instantânea de deslocamento ao longo do tempo. É um conceito que acrescenta grande precisão ao estudo do movimento. E é um avanço em relação à velocidade média, cuja informação é muito geral.

Para obter velocidade instantânea, vejamos um intervalo de tempo o menor possível. O cálculo diferencial é a ferramenta perfeita para expressar essa idéia matematicamente.

A velocidade instantânea é responsável pela velocidade móvel em cada ponto de sua rota. Fonte: Pixabay.

O ponto de partida é a velocidade média:

Agora vamos fazer uma abordagem Δt para 0 tudo o que pode. Este é um limite e o resultado será precisamente a velocidade instantânea:

Este limite é conhecido pelo nome da derivada. Na notação de cálculo diferencial que você tem:

Desde que o movimento seja restrito a uma linha reta, ele pode ser dispensado com a notação vetorial.

[TOC]

Cálculo de velocidade instantânea: interpretação geométrica

A figura a seguir mostra a interpretação geométrica do conceito de derivada: é a inclinação da linha tangente Para a curva x (t) vs. t Em cada ponto.

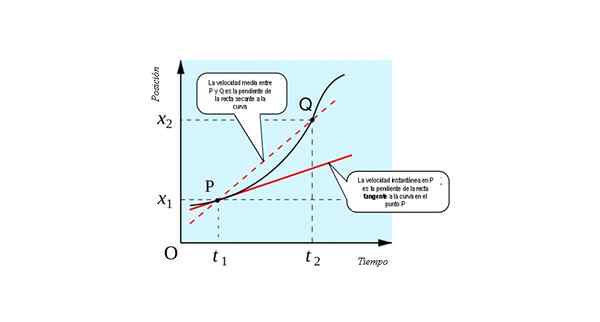A velocidade instantânea em P equivalente numericamente à inclinação da linha tangente à curva x vs. T no ponto P. Fonte: Fonte: すじにく シチュー [CC0].

Você pode imaginar como obter o limite se o ponto Q estiver se aproximando gradualmente. Chegará um momento em que os dois pontos estiverem tão próximos, que um não pode ser distinguido do outro.

A linha que os une será secando (reto que corta em dois pontos) para ser tangente (reto que toca a curva em um único ponto). Portanto, para encontrar a velocidade instantânea de uma partícula móvel, devemos ter:

• O gráfico da posição da partícula em função do tempo. Encontrando a inclinação da linha tangente à curva a cada momento, você tem a velocidade instantânea em cada ponto ocupado pela partícula.

Pode servir a você: Lei de Ampère: fórmula e equações, demonstração, exercícios

O bem:

• A função de posição de partícula x (t), que é derivado para obter a função de velocidade V (t), então esta função é avaliada em cada vez t, Uma conveniência. A função de posição deve ser derivável.

Alguns casos especiais no cálculo da velocidade instantânea

-A inclinação da linha tangente à curva em P é 0. Uma inclinação nula significa que o celular é interrompido e que sua velocidade é claro.

-A inclinação da linha tangente à curva em P é maior que 0. A velocidade é positiva. No gráfico acima, significa que o celular se afasta de ou.

-A inclinação da linha tangente à curva em P é menor que 0. A velocidade seria negativa. No gráfico acima, não há pontos como esse, mas nesse caso a partícula estaria se aproximando ou.

-A inclinação da linha tangente à curva é constante em p e todos os outros pontos. Nesse caso, o gráfico é uma linha reta e o celular tem movimento uniforme da linha MRU (sua velocidade é constante).

Em geral, a função V (t) É também uma função de tempo, que por sua vez pode ter derivado. E se não fosse possível encontrar aqueles derivados das funções x (t) e V (t)?

Em caso de x (t) Pode ser que a inclinação - a velocidade instantânea - mudou de sinais fortemente. Ou isso passará de zero para um valor diferente imediatamente.

Se sim x (t) Apresentaria dicas ou cantos nas mudanças repentinas. Muito diferente do caso representado na imagem anterior, na qual a curva x (t) É uma curva suave, sem pontos, cantos, descontinuidades ou mudanças abruptas.

Pode servir você: Bose Einstein Condensate

A verdade é que, para celulares reais, as curvas suaves são as que melhor representam o comportamento do objeto.

O movimento geral é bastante complexo. O celular pode ser parado por um tempo, acelere para passar do descanso para ter uma velocidade e se afastar do ponto de partida, manter a velocidade por um tempo, depois pare para parar novamente e, portanto, o estilo.

Eles podem começar de novo e continuar na mesma direção. Ou agir o revés e retornar. Isso é chamado de movimento variado em uma dimensão.

Abaixo, alguns exemplos do cálculo da velocidade instantânea esclarecerão o uso das definições dadas:

Exercícios de velocidade instantâneos resolvidos

Exercício 1

Uma partícula se move ao longo de uma linha reta com a seguinte lei de movimento:

x (t) = -t³ + 2 t² + 6 T - 10

Todas as unidades estão no sistema internacional. Encontrar:

a) a posição da partícula em t = 3 segundos.

b) A velocidade média no intervalo entre t = 0 se t = 3 s.

c) a velocidade média no intervalo entre t = 0 s e t = 3 s.

d) a velocidade instantânea da partícula da pergunta anterior, em t = 1 s.

Respostas

a) Para encontrar a posição da partícula, a lei de movimento (função de posição) em t = 3:

x (3) = (-4/3).3³ + 2. 3² ₊ 6.3 - 10 m = -10 m

Não há problema de que a posição seja negativa. O sinal (-) indica que a partícula está à esquerda da origem ou.

b) No cálculo da velocidade média, as posições finais e iniciais da partícula são necessárias nos tempos indicados: x (3) e x (0). A posição em t = 3 é x (3) e é conhecida sobre o resultado anterior. A posição em t = 0 segundos é x (0) = -10 m.

Pode atendê -lo: estático: história, que estudos, aplicações, leis

Como a posição final é a mesma que a inicial, conclui -se imediatamente que a velocidade média é 0.

c) A velocidade média é a razão entre a distância percorrida e o tempo gasto. Agora, a distância é o módulo ou magnitude do deslocamento, portanto:

Distância = | x2 - x1 | = | -10-(-10) | M = 20 m

Observe que a distância percorrida é sempre positiva.

v_{M = 20 m/3 s = 6.7 m/s}

d) Aqui é necessário encontrar a primeira derivada da posição em relação ao tempo. Então é avaliado por t = 1 segundo.

x '(t) = -4 t² + 4 T + 6

x '(1) = -4.1² + 4.1 + 6 m/s = 6 m/s

Exercício 2

Abaixo está o gráfico da posição de um celular em função do tempo. Encontre a velocidade instantânea em t = 2 segundos.

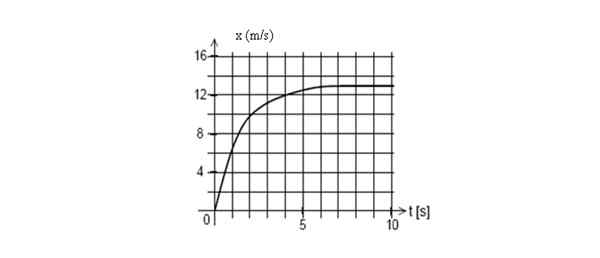Posicione o gráfico versus o tempo para um celular. Fonte: Self feito.

Responder

Desenhe a linha tangente para a curva em t = 2 segundos e calcule sua inclinação, levando dois pontos da linha.

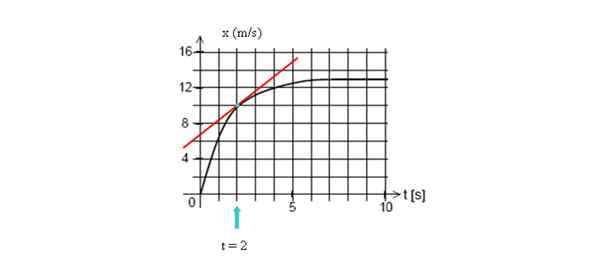Para calcular a velocidade instantânea indicada, desenhe a linha tangente para esse ponto e encontre sua inclinação. Fonte: Self feito.

Neste exemplo, levaremos dois pontos que são facilmente visualizados, cujas coordenadas são (2 s, 10 m) e o corte com o eixo vertical (0 s, 7 m):

Referências

1. Giancoli, d. Física. Princípios com aplicações. 6^º Edição. Prentice Hall. 22-25.
2. Resnick, r. (1999). Físico. Volume 1. Terceira edição em espanhol. México. Empresa Editorial Continental S.PARA. claro.V. 21-22.
3. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7^MA. Edição. México. Editores de aprendizado do Cengage. 23-25.