Vetores de unidade característicos, como divulgá -lo, exemplos

O vetores de unidade são aqueles cujo módulo, magnitude ou tamanho é igual ao valor numérico um. Os vetores da unidade são úteis para indicar a direção de outros vetores não unidades.

Lembre -se de que os vetores são entidades matemáticas que representam matematicamente as magnitudes físicas que dependem da direção, como força, velocidade, aceleração e outros.

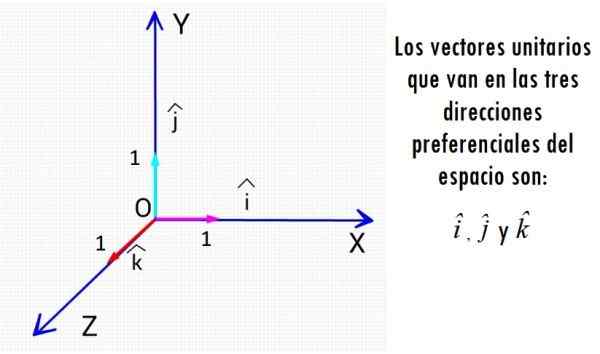
Os vetores de unidade mais conhecidos são os três vetores que vão nas direções dos eixos cartesianos. Fonte: f. Zapata.

Independentemente da magnitude física associada, os vetores da unidade são entidades sem unidades de medida e seu tamanho é sempre 1, um número puro.

Por exemplo, a velocidade de uma partícula que se move a 3 m/se segue na direção positiva do eixo x x é indicada: v = (3 m/s) Yo, onde a letra ousada é usada para denotar os valores do vetor. Neste exemplo, o módulo de v É 3 m/se o módulo de vetor unitário Yo é 1 (sem unidades).

[TOC]

Módulo, direção e significado

Dado o importante. No momento de representar uma quantidade de vetor, é necessário indicar claramente esses aspectos.

Agora, um vetor de unidade pode ter qualquer direção e o significado preferido, mas a magnitude deve sempre ser igual a 1.

Os vetores de unidade são usados ​​para indicar um endereço privado no espaço ou no plano. Se, por exemplo, precisamos trabalhar com todas as forças que agem ao longo do eixo horizontal, uma vez que um vetor de unidade nessa direção nos ajuda a distinguir essas forças de outras pessoas direcionadas em uma direção diferente.

E para distingui -los dos vetores não unidades, o BOLD é geralmente usado na impressão e coloca um sotaque circunflexo na parte superior, por exemplo:

Pode servir a você: Teoria Estado Estado: História, Explicação, Notícias

Para letras manuscritas, basta colocar o circunflejo para entender que é um vetor de unidade.

Características de um vetor de unidade

Matematicamente o vetor de unidade:

É um elemento que pertence a um espaço vetorial ℛ da dimensão n, de modo que |v| = 1, onde as barras significam "módulo".

Para que possamos estabelecer isso:

-O módulo vetorial unitário é sempre 1, não importa se é uma força, velocidade ou outro vetor.

-Os vetores da unidade têm uma certa direção, bem como a direção, como o vetor de unidade na direção vertical, que pode fazer sentido para cima ou para baixo.

-Os vetores de unidade têm um ponto de origem. Quando representado por um sistema de coordenadas cartesianas, o referido ponto coincide com a origem do sistema: (0,0) se for o plano ou (0.0.0) se o vetor estiver no espaço tridimensional.

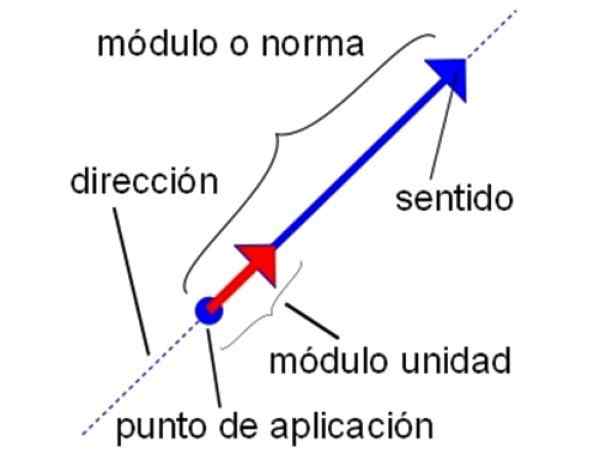As características do vetor da unidade. Fonte: Wikimedia Commons.

-Também com os vetores da unidade, todas as operações de soma, subtração e multiplicação de vetores que são feitas por vetores regulares podem ser realizadas. Portanto, é válido multiplicar o vetor da unidade por um escalar, além de executar o produto de ponto e o produto cruzado.

-Com um vetor de unidade em uma certa direção, outros vetores também podem ser expressos que também são orientados nessa direção.

Os vetores da unidade no espaço

Para expressar qualquer vetor no espaço ou no avião, você pode usar um conjunto de vetores unitários perpendiculares um ao outro, que formam uma base ortonormal. Cada uma das três direções preferenciais do espaço tem seu próprio vetor de unidade.

Vamos voltar ao exemplo das forças direcionadas ao longo do eixo horizontal. Este é o eixo x, que tem duas possibilidades: direção para a direita e direção para a esquerda. Suponha que haja um vetor de unidade no eixo X e direcionado para a direita, que podemos denotar através de qualquer uma dessas formas:

Pode servir a você: Thomson Atomic Model: características, postulações, partículas subatômicas

Qualquer um deles é válido. Agora, suponha uma força F₁ de magnitude 5 n ao longo deste eixo e direcionada para a direita, essa força poderia ser expressa como:

Se a força fosse direcionada ao longo do eixo x, mas na direção oposta, isto é, à esquerda, um sinal negativo poderia ser usado para estabelecer essa diferença.

Por exemplo, uma força de magnitude 8 n, localizada no eixo X e direcionada para a esquerda, seria assim:

Ou então:

E para vetores que não são direcionados ao longo dos eixos cartesianos, também há uma maneira de representá -los em termos dos vetores da unidade ortogonal, através de seus componentes cartesianos.

Como remover/calcular o vetor da unidade?

Para calcular o vetor unitário na direção de qualquer vetor arbitrário v, A fórmula a seguir é aplicada:

Onde:

É o módulo ou magnitude do vetor v, cujo quadrado é calculado assim:

|v|² = (v_x)² +  (v_e)²+  (v_z)²

Um vetor arbitrário em termos de vetor de unidade

Alternativamente, o vetor v Pode ser expresso da seguinte maneira:

Isto é, o produto de seu módulo pelo vetor de unidade correspondente. Isso é exatamente o que foi feito antes, ao falar sobre a força de 5 n de magnitude direcionada ao longo do eixo x positivo.

Representação gráfica

Graficamente, o que é dito é visto nesta imagem, onde o vetor v Está em azul e o vetor de unidade correspondente em sua direção está em vermelho.

Neste exemplo, o vetor v Tem uma magnitude maior que a do vetor da unidade, mas a explicação é válida se isso não acontecer. Em outras palavras, podemos ter vetores que são, por exemplo, 0.25 vezes o vetor da unidade.

Pode servir a você: Peso (físico): cálculo, unidades, exemplos, exercícios

Exemplos de vetores de unidade

Os vetores da unidade perpendicular I, J e K

Como já vimos antes, vetores unitários perpendiculares Yo, J e k Eles são muito úteis para representar qualquer outro vetor no avião ou espaço e realizar operações vetoriais. Em termos de referido vetor, um vetor arbitrário V é representado como:

v = v_x Yo + v_e J + v_z k

Onde V_x, v_e e V_z são os componentes retangulares do vetor v, que são escaladas -queol não são usadas para representá -las no texto impresso-.

Lei de Coulomb

Vetores unitários aparecem com frequência na física. Lá temos a lei de Coulomb, por exemplo, que descreve quantitativamente a interação entre duas cargas elétricas específicas.

Indica que a força F de atração ou repulsão entre essas cargas é proporcional ao produto delas, inversamente proporcional ao quadrado da distância que os separa e é direcionado na direção do vetor da unidade que une as cargas.

Este vetor é geralmente representado por:

E a lei de Coulomb é assim, em forma de vetor:

Onde k É a constante eletrostática, q₁ e q₂ Eles são as cargas e r É a distância que os separa.

Exercício resolvido

Encontre o vetor da unidade na direção do vetor v = 5Yo + 4J -8k, Dado em unidades arbitrárias.

Solução

A definição de vetor unitário acima é aplicada acima:

Mas primeiro você deve calcular o módulo vetorial, que, como possui três componentes, é determinado por:

|v|² = (v_x)² +  (v_e)² +  (v_z)²

Ficando:

|v|² = (5)² +  (4)² +  (-8)²= 25 + 16 + 64 = 105

Portanto, o módulo de v é:

|v| = √105

O vetor unitário pesquisado é simplesmente:

Isso finalmente nos leva a:

v = 0.488 Yo + 0.390 J - 0.781 k

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill.
2. Bedford, 2000. PARA. Mecânica para engenharia: estático. Addison Wesley.
3. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 1. Cinemática. Editado por Douglas Figueroa (USB).
4. Giambattista, a. 2010. Física. 2º. Ed. McGraw Hill.
5. Resnick, r. (1999). Físico. Vol. 1. 3ª ed. em espanhol. Empresa Editorial Continental S.PARA. claro.V.