Triângulo de Acutangle

O que são triângulos Acutangulus?

O Triângulos de Acutangulus Eles são aqueles cujos três ângulos internos são ângulos agudos; isto é, a medida de cada um desses ângulos é inferior a 90 °. Por não ter nenhum ângulo reto, temos que o teorema de Pitágoras não é atendido para esta figura geométrica.

Portanto, se queremos ter algum tipo de informação sobre qualquer um de seus lados ou ângulos, é necessário usar outros teoremas que nos permitam ter acesso a esses dados. Aqueles que podemos usar são o teorema da mama e o teorema de cosseno.

Características de um triângulo acutangle

Entre as características que essa figura geométrica possui, podemos destacar aqueles que são dados pelo simples fato de ser um triângulo. Entre eles, temos que:

- Um triângulo é um polígono que tem três lados e três ângulos.

- A soma de seus três ângulos internos é igual a 180 °.

- A soma de dois lados é sempre maior que a terceira.

Como exemplo, vamos ver o seguinte Triângulo ABC. Em geral, identificamos seus lados com letra minúscula e seus ângulos com letra maiúscula, para que um lado e seu ângulo oposto tenham a mesma letra.

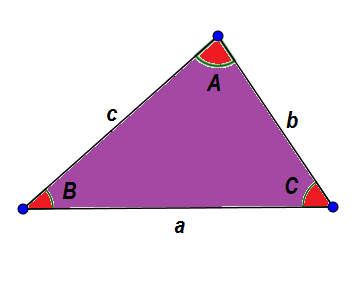
Por causa das características já dadas, sabemos que:

A + B + C = 180 °

A + B> C, A + C> B e B + C> A

A principal característica que distingue esse tipo de triângulo do resto é que, como já mencionamos, seus ângulos internos são agudos; isto é, a medida de cada um de seus ângulos é menor que 90 °.

Os triângulos de acutangulus, juntamente com os triângulos obtusos (aqueles em que um de seus ângulos tem uma medida maior que 90 °), fazem parte dos triângulos oblíquos conjuntos. Este conjunto é formado pelos triângulos que não são retângulos.

Pode atendê -lo: quais são os elementos da parábola? (Peças)

Ao fazer parte dos triângulos oblíquos, temos que resolver problemas em que os triângulos de acutangulus intervêm devem usar o teorema da mama e o teorema de cosseno.

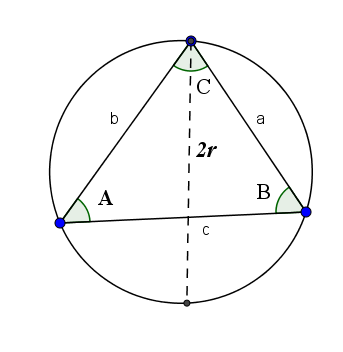
Teorema da mama

O teorema da mama afirma que a razão de um lado com o seio de seu ângulo oposto é igual a duas vezes o raio do círculo formado pelos três vértices do referido triângulo. Quer dizer:

2r = a/sin (a) = b/sen (b) = c/sen (c)

Teorema de Coseno

Por outro lado, o teorema de Coseno nos dá essas três igualidades para qualquer triângulo ABC:

para²= b² + c² -2bc*cos (a)

b²= a² + c² -2ac*cos (b)

c²= a² + b² -2ab*cos (c)

Esses teoremas também são conhecidos como a lei do seio e da lei de cosseno, respectivamente.

Outra característica que podemos dar de triângulos acutangulosos é que dois deles são os mesmos se atenderem a algum dos seguintes critérios:

• Se eles têm todos os três lados.
• Se eles tiverem um lado e dois ângulos iguais um ao outro.
• Se eles têm dois lados e um ângulo igual.

Tipos de triângulos acutángulos

Os triângulos acutangulus podem ser classificados de acordo com os lados. Estes podem ser:

Triangles acutangulos equiláteis

Eles são os triângulos acutangulosos que têm todos os seus lados iguais e, portanto, todos os seus ângulos internos têm o mesmo valor, que é a = b = c = 60 ° graus.

Como exemplo, vamos tomar o seguinte triângulo, cujos lados a, b e c têm um valor de 4.

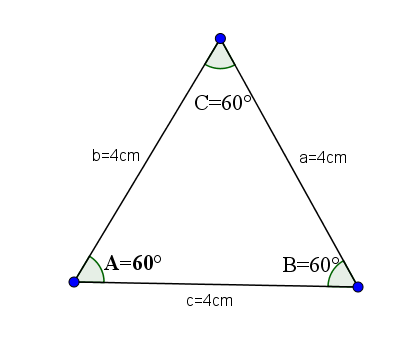
Isoceles acutángulos triângulos

Esses triângulos, além de ter ângulos internos agudos, têm a característica de ter dois de seus lados iguais e o terceiro, que geralmente é tomado como base, diferente.

Um exemplo desse tipo de triângulos pode ser aquele cuja base é 3 e seus outros dois lados têm um valor de 5. Com essas medidas, teria os ângulos opostos aos lados iguais com o valor de 72,55 ° e o ângulo oposto da base seria 34,9 °.

Pode servir a você: ângulo nulo: definição e características, exemplos, exercícios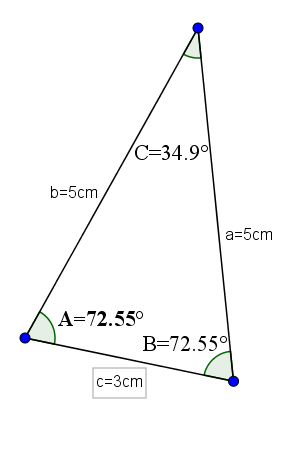

Triângulos de Scalene acutangulus

Estes são os triângulos que têm todos os seus lados diferentes dois a dois. Portanto, todos os seus ângulos, além de serem inferiores a 90 °, são diferentes dois a dois.

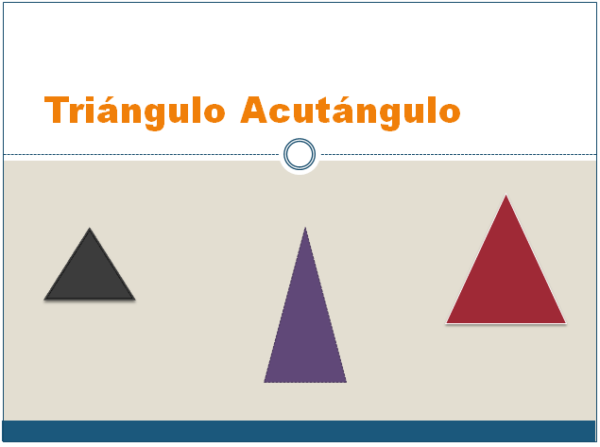
O triângulo def (cujas medidas são d = 4, e = 5 e f = 6 e seus ângulos são d = 41,41 °, e = 55,79 ° e F = 82,8 °) é um bom exemplo de um triângulo de acutangle scalenonene.

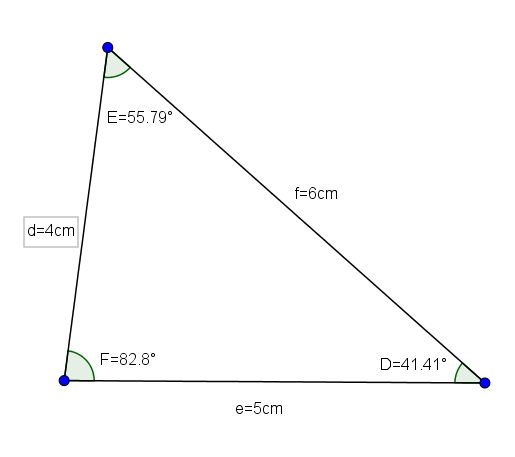
Resolução dos triângulos de Acutangles

Como dissemos anteriormente, para a resolução de problemas em que os triângulos acutangulus intervêm.

Exemplo 1

Dado um triângulo ABC com ângulos A = 30 °, B = 70 ° e lado a = 5 cm, queremos saber o valor do ângulo C e os lados B e C.

A primeira coisa que fazemos é usar o fato de que a soma dos ângulos internos de um triângulo é 180 °, a fim de obter o valor do ângulo C.

180 ° = a + b + c = 30 ° + 70 ° + c = 100 ° + c

Nós limpamos C e temos:

C = 180 ° - 100 ° = 80 °

Como conhecemos os três ângulos e um lado, podemos usar o teorema da mama para determinar o valor dos lados restantes. Para o teorema, temos que:

a/sin (a) = b/sen (b) e a/sen (a) = c/(sin (c)

Limparemos a equação e temos que:

B = (a*sin (b))/sin (a) ≈ (5*0.940) / (0.5) ≈ 9.4

Agora só precisamos calcular o valor de C. Prosseguimos análogos como no caso anterior:

C = (a*sin (c))/sin (a) ≈ (5*0.984)/(0.5) ≈ 9.84

Assim, obtemos todos os dados do triângulo. Como podemos notar, este triângulo entra na categoria Triângulo de varredura.

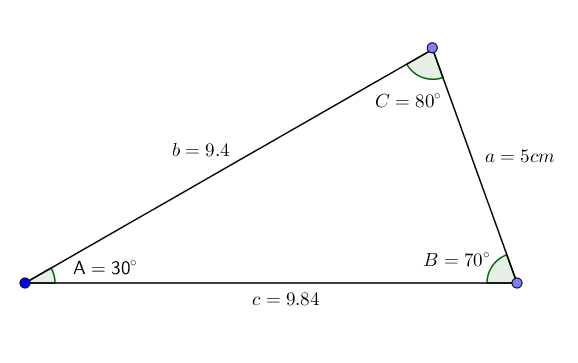
Exemplo 2

Dado um triângulo de defesa com os lados d = 4cm, e = 5cm e f = 6cm, queremos saber o valor dos ângulos do referido triângulo.

Para este caso, usaremos a lei do cosseno, que nos diz que:

Pode atendê -lo: soma dos quadrados de dois números consecutivos

d²= e² + F² - 2efcos (D)

A partir desta equação, podemos limpar cos (d), que resulta em:

Cos (d) = ((4)² - (5)² -(6)²)/(-2*5*6) = 0.75

A partir daqui, temos que dock 41.41 °

Usando o teorema do Senom agora, temos a seguinte equação:

D/(sin (d) = e/(sin (e)

Limpando sen (e), temos que:

sin (e) = e*sen (d)/d = (5*0.66)/4 ≈ 0.827

Daqui temos que.79 °

Finalmente, usando que a soma dos ângulos internos de um triângulo é 180 °, temos que.8 °.