Características de trajetória física, tipos, exemplos e exercícios

O Trajetória em física É a curva que descreve um celular ao passar por pontos sucessivos durante seu movimento. Como isso pode adotar inúmeras variantes, elas também serão as trajetórias que o celular pode seguir.

Para ir de um lugar para outro, uma pessoa pode seguir caminhos diferentes e maneiras diferentes: a pé pelas calçadas em ruas e avenidas, ou chegar de carro ou motocicleta em uma rodovia. Durante uma viagem pela floresta, o andador pode seguir uma trajetória complicada que inclui curvas, escalando ou caindo e até que ele passe várias vezes pelo mesmo ponto.

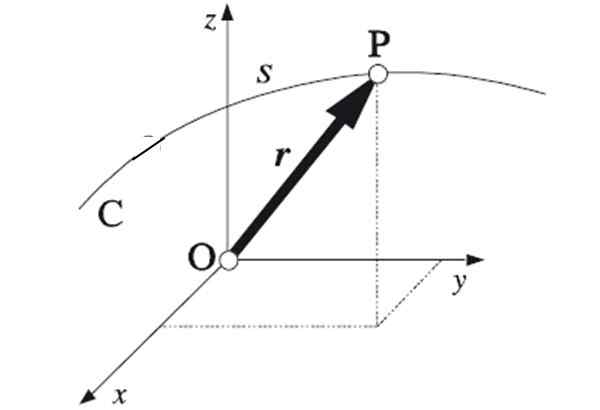figura 1. Juntando -se aos pontos extremos de cada vetor de posição, a trajetória seguida pela partícula é obtida. Fonte: Algarabia [domínio público]

Se os pontos pelos quais o celular está viajando seguir uma linha reta, a trajetória será retilínea. Esta é a trajetória mais simples, por ser uma dimensão. Especificar a posição requer uma única coordenada.

Mas o celular pode seguir uma trajetória de curvil, podendo ser fechada ou aberta. Nesses casos, o monitoramento da posição requer duas ou três coordenadas. Estes são movimentos no avião e espaço, respectivamente. Isso tem a ver com links: Limitando as condições materiais do movimento. Alguns exemplos são:

- As órbitas que descrevem os planetas ao redor do sol são trajetórias em forma de elipse fechadas. Embora, em alguns casos, eles possam se aproximar de uma circular, como no caso da terra.

- A bola que o goleiro chuta em um chute de gol segue uma trajetória parabólica.

- Um pássaro em voo descreve trajetórias curvilíneas no espaço, porque, além de se mover em um avião, pode subir ou mais baixo à vontade.

A trajetória de física pode ser expressa matematicamente quando a posição de celular é conhecida a qualquer momento. Ser r O vetor de posição, que por sua vez tem coordenadas x, e e z No caso mais geral de um movimento tridimensional. Conhecendo a função r (T) A trajetória será completamente determinada.

[TOC]

Pessoal

Em termos gerais, a trajetória pode ser uma curva bastante complicada, especialmente se você quiser expressar matematicamente. Portanto, começa com os modelos mais simples, onde os celulares viajam em uma linha reta ou em um avião, que pode ser o piso ou qualquer outro adequado:

Movimentos em um, duas e três dimensões

As trajetórias mais estudadas são:

- Retilíneo, Ao viajar em uma linha horizontal, vertical ou inclinada. Uma bola jogada verticalmente para cima desta trajetória ou um objeto que escorrega ladeira abaixo por um plano inclinado também. Eles são movimentos dimensionais, uma única coordenada é suficiente para determinar sua posição completamente.

- Parabólico, em que o celular descreve um arco de parábola. É frequente, uma vez que qualquer objeto lançado obliquamente sob a ação da gravidade (um projétil) segue esta trajetória. Para especificar a posição móvel, você deve dar duas coordenadas: x e e.

- Circular, ocorre quando a partícula em movimento segue uma circunferência. Também é comum na natureza e na prática diária. Muitos objetos diários seguem uma trajetória circular, como pneus, peças de máquinas e satélites em órbita, para dar alguns exemplos.

Pode atendê -lo: vetores de equipamentos: definição, notação, exercícios

- Elíptico, O objeto se move após uma elipse. Como afirmado no início, é a trajetória que os planetas seguem em órbita ao redor do sol.

- Hiperbólico, Objetos astronômicos sob a ação de uma força central (gravidade), podem seguir trajetórias elípticas (fechadas) ou hiperbólicas (abertas), estas são menos frequentes que as primeiras.

- Helicoidal, o movimento espiral, como o de um pássaro que sobe em uma corrente térmica.

- Influência ou pendular, O celular descreve um arco em movimentos de ida e volta.

Exemplos

As trajetórias descritas na seção anterior são muito úteis para ter uma idéia rapidamente de como os movimentos de um objeto são. De qualquer forma, é necessário esclarecer que a trajetória de um celular depende da localização do observador. Isso significa que o mesmo evento pode ser visto de maneiras diferentes, de acordo com onde cada um está.

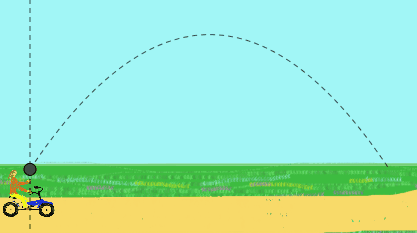
Por exemplo, uma garota pedal em velocidade constante e joga uma bola para cima. Ela observa que a bola descreve uma trajetória retilínea. 

No entanto, para um observador em pé na estrada que o vê, a bola terá um movimento parabólico. Para ele, a bola foi inicialmente jogada com uma velocidade inclinada, o resultado da velocidade na mão da garota e a velocidade da bicicleta.

Figura 2. Esta animação mostra o lançamento vertical de uma bola feita por uma garota que passa de bicicleta, como ela vê (trajetória retilínea) e como você vê um observador (trajetória parabólica). (Preparado por f. Zapata).

Trajetória de um celular de uma maneira explícita, implícita e paramétrica

- Explícito, especificando diretamente a curva ou local geométrico dado pela equação e (x)

- Implícito, em que uma curva é expressa como f (x, y, z) = 0

-Paramétrico, Dessa maneira t. Nesse caso, a trajetória consiste nas funções: x (t), e T) e z (t).

Em seguida, duas trajetórias muito estudadas são detalhadas na cinemática: a trajetória parabólica e a trajetória circular.

Lançamento em um vácuo

Um objeto (o projétil) é jogado formando um ângulo A com a horizontal e com uma velocidade inicial v_qualquer Como a imagem mostra. A resistência do ar não é levada em consideração. O movimento pode ser tratado como dois movimentos independentes e simultâneos: um horizontal com constante e outra velocidade vertical sob a ação da gravidade.

x (t) = x_qualquer +v_boi.t

e (t) = y_qualquer +v_Oy.T -½g.t²

Essas equações são Equações paramétricas do lançamento do projétil. Como explicado acima, eles têm parâmetro comum t, que é o tempo.

No triângulo certo da figura, o seguinte pode ser visto:

v_boi = v_qualquer cos θ_Yo

v_Oy = v_qualquer sin θ_Yo

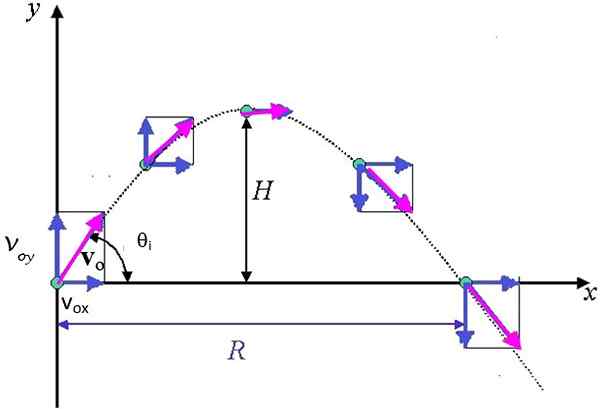Figura 3. Trajetória parabólica seguida de um projétil, que mostra os componentes do vetor de velocidade. H é a altura máxima e R é o alcance horizontal máximo. Fonte: AYUSH12GUPTA [CC BY-SA 4.0 (https: // CreativeCommons.Org/licenças/BY-SA/4.0)]

Ao substituir essas equações que contêm o ângulo de lançamento nas equações paramétricas, é:

Pode servir a você: Difração do som: o que é, exemplos, aplicações

x (t) = x_qualquer +v_qualquer cos θ_Yo.t

e (t) = y_qualquer +v_qualquer. sin θ_Yo.T -½g.t²

Equação de trajetória parabólica

A equação explícita da trajetória está limpando t da equação para x (t) e substituindo a equação y (t) (t). Para facilitar o trabalho algébrico, pode -se assumir que a origem (0,0) está no ponto de lançamento e dessa maneira x_qualquer = y_qualquer = 0.

Depois de simplificar o parâmetro "t”Foi eliminado e a equação que permanece é e dependendo de x: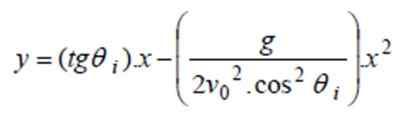

Esta é a equação de trajetória em Forma explícita.

Trajetória circular

Uma trajetória circular é dada por:

(X - x_qualquer)² + (e e_qualquer)² = R²

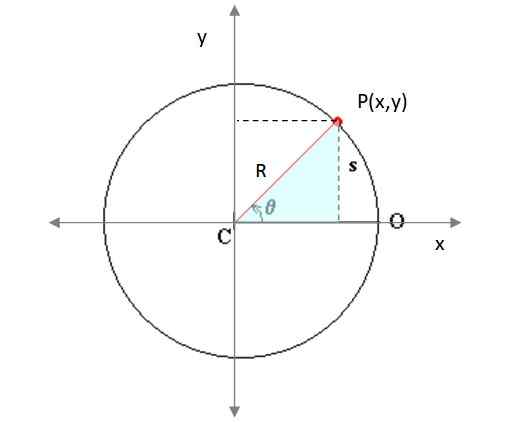Figura 4. Uma partícula se move em uma trajetória circular no avião. Fonte: modificado por f. Sapato da Wikimedia Commons.

Aqui x_qualquer e e_qualquer Eles representam o centro da circunferência descrito pelo celular e r é o raio do mesmo. P (x, y) é um ponto da trajetória. Do triângulo retângulo sombreado (Figura 3), é avisado de que:

x = r. cos θ

y = r. sin θ

O parâmetro, neste caso, é o ângulo de varredura θ, chamado deslocamento angular. No caso particular de que a velocidade angular ω (ângulo varrida por unidade de tempo) é constante, pode -se afirmar que:

θ = θ_qualquer + Ωt

Onde θ_qualquer É a posição angular inicial da partícula, que se tomada como 0, é reduzida a:

θ = ωt

Nesse caso, o tempo retorna a equações paramétricas como:

x = r.cos ωt

y = r. sin ωt

Os vetores da unidade Yo e J Eles são muito convenientes para escrever a função de posição de um objeto r (T). Eles indicam as instruções no eixo x E no eixo e respectivamente. Em seus termos, a posição de uma partícula que descreve um movimento circular uniforme é:

r (t) = r.cos ωt Yo + R. sin ωt J

Exercícios resolvidos

Exercício resolvido 1

Um canhão pode disparar uma bala com uma velocidade de 200 m/se um ângulo de 40º em relação à horizontal. Se o lançamento for realizado em terreno plano e a resistência do ar é desprezada, encontre:

a) A equação de trajetória e (x) ..

b) as equações paramétricas x (t) e e T).

c) o alcance horizontal e o tempo em que o projétil dura no ar.

d) a altura em que o projétil está localizado quando x = 12.000 m

Solução para)

a) Para encontrar a trajetória, os valores fornecidos na equação y (x) da seção anterior são substituídos:

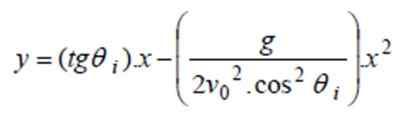
e (x) = TG 40º. x - 9.8/(2 '400². cos²40º) x² ⇒  e (x) = 0.8391 x - 0.0000522X²

Solução b)

b) O ponto de lançamento é escolhido na origem do sistema de coordenadas (0,0):

x (t) = x_qualquer +v_boi.T = 400'Cos 40º.T = 306.42. t.

e (t) = y_qualquer +v_Oy.T -½g.t²= 400 'Sen 40º.T - 0.5 '9.8'T²= 257.12 T - 4.9.t²

Solução c)

c) Para encontrar o tempo que o projétil dura no ar, é feito e (t) = 0, Sendo o lançamento, é feito em terreno plano:

Pode atendê -lo: o que é relativa e absoluta aspereza?

0 = 257.12.T - 4.9.t²

T = 257.12/4.9 s = 52.473 s

O escopo máximo horizontal está substituindo esse valor em x (t):

x_Máx = 306.42'52.47 m = 16077.7 m

Outra maneira de encontrar x_Máx Está fazendo diretamente y = 0 na equação de trajetória:

0 = 0.8391 x_Máx - 0.0000522 x²_Máx

x = 0.8391 /0.0000522 m = 16078.5m

Há uma pequena diferença devido ao arredondamento de decimais.

D) solução

d) Para saber a altura quando x = 12000 m esse valor é substituído diretamente na equação de trajetória:

e (12000) = 0.8391'12000 - 0.0000522'12000² M = 2552.4 m

Exercício resolvido 2

A função de posição de um objeto é dada por:

r (t) = 3t Yo + (4 -5t²) J m

Encontrar:

a) A equação para a trajetória. Que curva é?

b) a posição inicial e a posição quando t = 2 s.

c) o deslocamento feito após t = 2 s.

Solução

a) A função de posição foi dada em termos de vetores da unidade Yo e J, que determinam respectivamente o endereço nos eixos x e e, portanto:

x (t) = 3t

e T) = 4 -5t²

A equação de trajetória e (x) Ele está limpando t de x (t) e substituindo e T):

T = x/3

e (x) = 4 -5. (X/3)² = 4 - 5x²/9 (parábola)

b) A posição inicial é: r (2) = 4 J m ; A posição em T = 2 s é r (2) = 6 Yo -16 J m

c) Deslocamento Dr É a subtração dos dois vetores de posição:

Δr = r (2) - r (2) = 6 Yo -16 J- 4 J = 6 Yo - vinte J m

Exercício resolvido 3

A Terra tem um raio r = 6300 km e sabe -se que o período de rotação de seu movimento em torno de seu eixo é um dia. Encontrar:

a) A equação da trajetória de um ponto na superfície da Terra e sua função de posição.

b) a velocidade e a aceleração do referido ponto.

Solução para)

a) A função de posição para qualquer ponto em órbita circular é:

r (t) = r.cos ωt Yo + R.sin ωt J

Você tem o raio da terra r, mas não a velocidade angular ω, no entanto, pode ser calculada a partir do período, sabendo que, para o movimento circular, é válido dizer que:

Ω = 2π × Frequência = 2π / período

O período de movimento é: 1 dia = 24 horas = 1440 minutos = 86400 segundos, portanto:

Ω =  2π / 86400 s = 0.000023148 ​​s^-1

Substituindo na função de posição:

r (t) = r.cos ωt Yo + R. sin ωt J = 6300 (cos 0.000023148T Yo + sin 0.000023148T J) KM

O caminho em uma forma paramétrica é:

x (t) = 6300. cos 0.000023148T

e (t) = 6300. sin 0.000023148T

Solução b)

b) Para o movimento circular, a magnitude da velocidade linear v de um ponto está relacionado à velocidade angular C através:

v = ΩR = 0.000023148 ​​s^-1'6300 km = 0.1458 km/s = 145.8 m/s

Mesmo sendo um movimento constante de 145.8 m/s, Há uma aceleração que aponta para o centro da órbita circular, responsável por manter o ponto na rotação. É aceleração centrípeta para_c, dado por:

para_c = v² / R = (145.8 m/s)² / 6300 × 10³ M = 0.00337 m/s².

Referências

1. Giancoli, d. Física. (2006). Princípios com aplicações. 6^º Prentice Hall. 22-25.
2. Kirkpatrick, l. 2007. Física: uma olhada no mundo. 6^ta Edição abreviada. Cengage Learning. 23 - 27.
3. Resnick, r. (1999). Físico. Volume 1. Terceira edição em espanhol. México. Empresa Editorial Continental S.PARA. claro.V. 21-22.
4. Rex, a. (2011). Fundamentos da Física. Pearson. 33 - 36
5. Sears, Zemansky. (2016). Física da Universidade com Física Moderna. 14^º. Ed. Volume 1. 50 - 53.
6. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7^MA. Edição. México. Editores de aprendizado do Cengage. 23-25.
7. Serway, r., Vulle, c. (2011). Fundamentos da Física. 9^{n / D} Ed. Cengage Learning. 43 - 55.
8. Wilson, J. (2011). Física 10. Pearson Education. 133 - 149.