Fourier Discreet Propriedades transformadas, aplicações, exemplos

O Fourier discreet transformado É um método numérico usado para definir amostras relacionadas às frequências espectrais que compõem um sinal. Estuda funções periódicas em parâmetros fechados, jogando como resultado outro sinal discreto.

Para obter a transformação discreta de furier de n pontos, em um sinal discreto, as duas condições a seguir em uma sequência devem ser atendidas X [n]

 x [n] = 0   N n - 1

Cumprindo essas condições, a transformação discreta de Fourier pode ser definida como

TDF

A transformação discreta de Fourier pode ser definida como uma amostragem em n pontos da transformação de Fourier.

[TOC]

Interpretação da transformação discreta de Fourier

Fonte: pexels

Existem 2 pontos de vista dos quais os resultados obtidos em uma sequência x podem ser interpretados_s[n] através da transformação discreta de Fourier.

-O primeiro corresponde aos coeficientes espectrais, já conhecidos pela série Fourier. É observado em sinais periódicos discretos, com amostras coincidindo com a sequência x_s[N].

-O segundo é sobre o espectro de um sinal Aperiadic Discreet, com amostras correspondentes à sequência x_s[N].

A transformação discreta é uma abordagem para o espectro do sinal analógico original. Sua fase depende de momentos de amostragem, enquanto sua magnitude depende do intervalo de amostragem.

Propriedades

Os fundamentos algébricos da estrutura compõem a base lógica das seções a seguir.

Linearidade

C . S_n → c . F [S_k]; Se uma sequência for multiplicada por um escalar, sua transformação também será.

T_n + V_n = F [t_k]+F [v_k]; A transformação de uma soma é igual à soma dos transformados.

Dualidade

F [s_n] → (1/n) s_-K; Se a transformação discreta de Fourier for recuperada em uma expressão já transformada, a mesma expressão é obtida, subindo em n invertido em relação ao eixo vertical.

Convolução

Perseguindo objetivos semelhantes que, no Laplace Transform, a convolução das funções refere -se ao produto entre suas transformações de Fourier. A convolução também se aplica a tempos discretos e é responsável por muitos procedimentos modernos.

X_n * R_n → F [x_n] .F [r_n]; A transformação de uma convolução é igual ao produto daqueles transformados.

X_n . R_n→ F [x_n] * F [r_n]; A transformação de um produto é igual à convolução dos transformados.

Deslocamento

X_N-m → F [x_k] e ^{-I (2π/n) km} ; Se uma sucessão for atrasada nas amostras M, seu efeito na transformação discreta será uma modificação do ângulo definido por (2π/n) km.

Pode atendê -lo: por que a álgebra é importante em certas situações da vida cotidiana?

Simetria conjugado

X_t [-K] = x*_t[k] = x_t [N - k]

Modulação

C^-nm_N . x [n] ↔ x_t[K - M]

produtos

x [n] y [n] ↔ (1/n) x_t[k]*e_t[K]

Simetria

X [-n] ↔ x_t[-K] = x*_t[K]

Conjugado

x*[n] ↔ x*_t[-K]

Equação parseval 

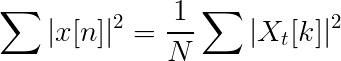
Semelhanças e diferenças com a transformação de Fourier

Com relação ao transformal convencional de Fourier, ele tem várias semelhanças e diferenças. A transformação de Fourier converte uma sequência em uma linha contínua. Dessa maneira, diz -se que o resultado da variável de Fourier é uma função de variável real complexa.

A transformação discreta de Fourier, ao contrário, recebe um sinal discreto e o transforma em outro sinal discreto, ou seja, uma sequência.

Qual é o uso da transformação discreta de Fourier?

Eles servem principalmente para equações significativas, enquanto transformam expressões derivadas em elementos de poder. Denotando expressões diferenciais em formas de polinômios integráveis.

Na otimização, modulação e modelagem de resultados, ele atua como uma expressão padronizada, sendo um recurso frequente para a engenharia após várias gerações.

Fonte: Pixabay

História

Este conceito matemático foi apresentado por Joseph B. Fourier em 1811, enquanto desenvolve um tratado sobre o Espalhe calor. Foi rapidamente adotado por vários ramos da ciência e engenharia.

Foi estabelecido como a principal ferramenta de trabalho no estudo de equações com derivados parciais, comparando mesmo com a relação de trabalho entre o Laplace transformou e equações diferenciais comuns.

Qualquer função que possa ser trabalhada com a transformação de Fourier deve apresentar a nulidade fora de um parâmetro definido.

Fourier discreet transformado e seu inverso

A transformação discreta é obtida através da expressão:

Após uma sequência discreta x [n]

O inverso da transformação discreta de Fourier é definido através da expressão:

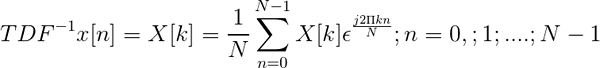TDF inverso

Permite que, uma vez que o discreto transformado, defina a sequência no domínio do tempo x [n].

Farily

O processo de parametrização correspondente à transformação discreta de Fourier está no filho. Para trabalhar a transformação, devemos limitar a sequência no tempo. Em muitos casos, os sinais em questão não têm essas limitações.

Uma sucessão que não atende aos critérios de tamanho a ser aplicada à transformação discreta, pode ser multiplicada por uma função "janela" v [n], definindo o comportamento da sucessão em um parâmetro controlado.

Pode atendê -lo: permutações circulares: demonstração, exemplos, exercícios resolvidos

X [n] . V [n]

A largura do espectro dependerá da largura da janela. À medida que a largura da janela aumenta, os transformados calculados serão mais estreitos.

Formulários

Cálculo da solução fundamental

A transformação discreta de Fourier é uma ferramenta poderosa no estudo de sucessões discretas.

A transformação discreta de Fourier transforma uma função variável contínua, em uma transformação de variável discreta.

O problema de Cauchy para a equação de calor apresenta um campo frequente de aplicação da transformação discreta de Fourier. Onde a função é gerada Dirichlet Heat ou núcleo do núcleo, que se aplica à amostragem de valores em um parâmetro definido.

Teoria do sinal

A razão geral para a aplicação da transformação discreta de Fourier nesse ramo se deve principalmente à decomposição característica de um sinal como uma sobreposição infinita de sinais mais facilmente tratáveis.

Pode ser uma onda sonora ou uma onda eletromagnética, a transformação discreta de Fourier expressa em uma simples sobreposição de ondas. Esta representação é bastante frequente em engenharia elétrica.

Série de Fourier

Eles são séries definidas em termos de cosenos e seios. Eles servem para facilitar o trabalho com funções periódicas gerais. Quando aplicados, eles fazem parte das técnicas de resolução de equações diferenciais parciais e comuns.

As séries de Fourier são ainda mais gerais que a série de Taylor, porque desenvolvem funções periódicas de descontinua que não têm representação na série Taylor.

Outras formas da série Fourier

Para entender analiticamente a transformação de Fourier, é importante.

-Série de Fourier em uma função do período 2L:

Muitas vezes é necessário adaptar a estrutura de uma série de Fourier, a funções periódicas cujo período é p = 2l> 0 no intervalo [-l, l].

-Série de Fourier em funções pares e estranhas

O intervalo [-π, π] é considerado que oferece vantagens ao aproveitar as características simétricas das funções.

Pode atendê -lo: conjunto finito: propriedades, exemplos, exercícios resolvidos

Se f é torque, a série Fourier é estabelecida como uma série de cosenos.

Se F é estranho, a série Fourier é estabelecida como uma série de seios.

-Notação complexa da série Fourier

Se você tem uma função f (t), que atende a todos os requisitos da série Fourier, é possível denotá-lo no intervalo [-t, t] usando sua notação complexa: 

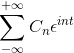
Exemplos

Em relação ao cálculo da solução fundamental, são apresentados os seguintes exemplos:

Equação de Laplace

Equação de calor

Equação de Schrödinger

Equação de onda

Por outro lado, existem exemplos de aplicação da transformação discreta de Fourier no campo da teoria dos sinais:

-Problemas de identificação do sistema. Estabelecido f e g

-Problema com a consistência do sinal de saída

-Problemas com a filtragem de sinal

Exercícios

Exercício 1

Calcule a transformação discreta de Fourier para a seguinte sucessão.

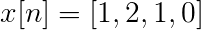
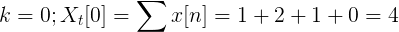
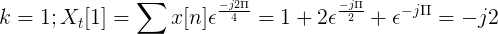
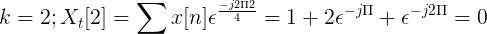
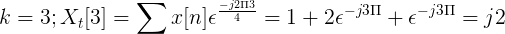
O x [n] tdf pode ser definido como:

X_t[k] = 4, -j2, 0, j2 para k = 0, 1, 2, 3

Exercício 2

É desejado determinar através de um algoritmo digital o sinal espectral definido pela expressão x (t) = e^-t. Onde a frequência máxima que solicita o coeficiente é f_m= 1hz. Um harmônico corresponde a F = 0.3 Hz. O erro é limitado a menos de 5%. Calcular F_s , D e n.

Levando em consideração o teorema da amostragem F_s = 2f_m = 2 Hz

Uma resolução de frequência de F₀ = 0.1 Hz, onde d = 1/0,1 = 10s são obtidos

0.3 Hz é a frequência correspondente ao índice k = 3, onde n = 3 × 8 = 24 amostras. Indicando que F_s = N/d = 24/10 = 2.4> 2

Como o objetivo é alcançar o menor valor possível para n, os seguintes valores podem ser considerados como uma solução:

F₀ = 0.3 Hz

D = 1/0.3 = 3.33s

K = 1

N = 1 × 8 = 8

Referências

1. Dominando a transformação discreta de Fourier em um, duas ou várias dimensões: armadilhas e artefatos. Isaac Amidor. Springer Science & Business Media, 19 de julho. 2013
2. O Manual do DFT: um proprietário para a transformação discreta de Fourier. William l. Briggs, van Emden Henson. Siam, 1 de janeiro. novecentos e noventa e cinco
3. Processamento de sinal digital: teoria e prática. D. Sundararajan. World Scientific, 2003
4. Transformações e algoritmos rápidos para análise e representações de sinal. Guoan BI, Yonghong Zeng. Springer Science & Business Media, 6 de dezembro. 2012
5. Transformações discretas e contínuas de Fourier: análise, aplicações e algoritmos rápidos. Eleanor Chu. CRC Press, 19. 2008