Fórmulas de tiro vertical, equações, exemplos

Ele tiro vertical É um movimento que ocorre sob a ação de um campo de forças, geralmente o da gravidade, sendo capaz de estar ascendente ou descendente. Também é conhecido pelo nome de Lançamento vertical.

O exemplo mais imediato é lançado (ou para baixo se preferir) uma bola com a mão, sim, certifique -se de fazê -lo verticalmente. Desperendo a resistência do ar, o movimento que segue a bola se encaixa perfeitamente no modelo de movimento retilíneo (MRUV) variado uniformemente variado (MRUV).

figura 1. Falar uma bola verticalmente para cima é um bom exemplo de tiro vertical. Fonte: pexels.

O tiro vertical é um movimento amplamente estudado nos cursos introdutórios da física, pois é uma amostra do movimento em uma dimensão, Um modelo muito simples e útil.

Este modelo pode não ser usado apenas para estudar a cinemática dos objetos sob a ação da gravidade, mas também, como será visto mais tarde, descreve o movimento de partículas no meio de um campo elétrico uniforme.

[TOC]

Fórmulas e equações

A primeira coisa que é necessária é um sistema de coordenadas para indicar a origem e rotulá -lo com uma letra, que no caso de movimentos verticais é a letra "e".

Então o sentido positivo é selecionado +e, o que geralmente é um significado -e Isso geralmente é retirado (veja a Figura 2). Tudo isso, a menos que quem resolva o problema decide o contrário, já que outra opção é levar como positivo a direção do movimento, qualquer que seja.

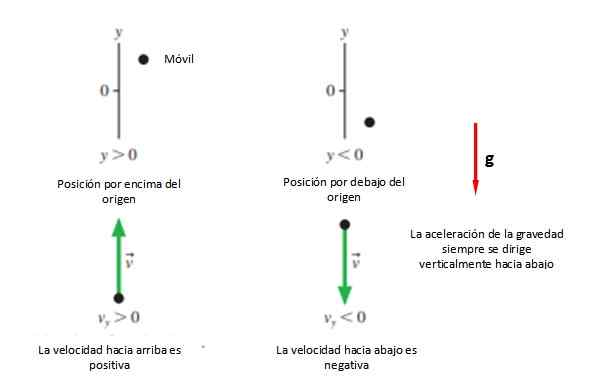Figura 2. Convenção de sinais usuais no tiro vertical. Fonte: f. Zapata.

De qualquer forma, recomenda -se que a origem coincide com o ponto do lançamento e_qualquer, Porque as equações são simplificadas, embora qualquer posição que seja desejada possa ser levada para começar a estudar o movimento.

Pode servir a você: Segundo Equilíbrio Condição: Explicação, Exemplos, Exercícios

Equações de tiro vertical

Depois que o sistema de coordenadas e a origem foram estabelecidos, vamos às equações. As magnitudes que descrevem o movimento são:

-Velocidade inicial v_qualquer

-Aceleração para

-Velocidade v

-Posição inicial x_qualquer

-Posição x

-Deslocamento Dx

-Tempo t

Todos, exceto o tempo, são vetores, mas como é um movimento unidimensional com uma certa direção, que importa então está usando sinais de + ou - para apontar para onde a magnitude em questão é direcionada. No caso de tiro vertical, a gravidade sempre cai e, a menos que especificado de outra forma, um sinal é concedido -.

Existem então as equações adaptadas para o tiro vertical, substituindo "x" por "e" e "para" por "g". Além disso, o sinal (-) correspondente à gravidade direcionada para baixo:

1) Posição: y = y_qualquer + v_qualquer.T - ½ g.t²

2) velocidade: v = v_qualquer - g.t

3) velocidade dependendo do deslocamento δe: v² = v_qualquer² - 2.g. Δe

Exemplos

Depois, há exemplos de aplicação para disparos verticais. Em sua resolução, o seguinte deve ser levado em consideração:

-"g”Tem um valor constante que, em média, é 9,8 m/s² ou aproximadamente 10 m/s² Se preferir facilitar os cálculos quando não for necessário muito.

-Quando v_qualquer OK 0, Essas equações são reduzidas às de queda livre.

-Se o lançamento acabar, o objeto precisará ter uma velocidade inicial que permita que você se mova. Uma vez em movimento, o objeto atinge uma altura máxima que dependerá do tamanho da velocidade inicial. É claro que, em maior altura, o celular passará mais tempo no ar.

-O objeto retorna ao ponto de partida com a mesma velocidade com que foi lançado, mas a velocidade é direcionada para baixo.

-Para um lançamento vertical, quanto maior a velocidade inicial, mais cedo o objeto chegará ao chão. Aqui a distância percorrida é fixada de acordo com a altura selecionada para o lançamento.

Pode atendê -lo: o que é relativa e absoluta aspereza?

-Na foto vertical, o tempo que leva o celular para atingir a altura máxima é calculado fazendo v = 0 Na equação 2) da seção anterior. Este é ele tempo máximo t_Máx:

0 = v_qualquer - g . t_Máx ⇒ t_Máx = v_qualquer /g

-O altura máxima e_Máx Limpa da equação 3) da seção anterior também fazendo v = 0:

0 = v_qualquer² - 2.g. Δy ⇒ 0 = V_qualquer² - 2.g. (e_Máx - e_qualquer) ⇒ e_Máx = y_qualquer  + v_qualquer² / 2 g

Sim e_qualquer = 0, É reduzido para:

e_Máx = v_qualquer² / 2 g

Exemplo 1 resolvido 1

Uma bola com V é jogada verticalmente para cima_qualquer = 14 m/s, do topo de um edifício de 18 m de altura. A bola pode seguir o seu jusante até a calçada. Calcular:

a) A altura máxima atingida pela bola em relação ao solo.

b) o tempo no ar (hora do voo).

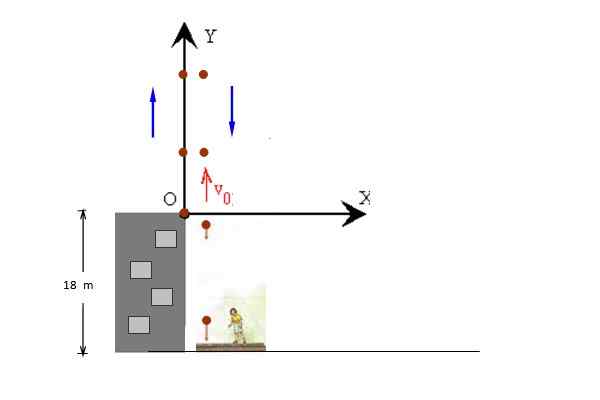Figura 3. Uma bola é jogada verticalmente do teto de um prédio. Fonte: f. Zapata.

Solução

Na figura, os movimentos de ascensão e abaixamento da bola aparecem separadamente para clareza, mas ambos acontecem na mesma linha. A posição inicial é tomada em y = 0, para que a posição final seja y = - 18 m.

a) A medida máxima medida a partir do teto do edifício é e_Máx = v_qualquer² / 2 g E a partir da declaração, é lido que a velocidade inicial é de +14 m/s, então:

e_Máx = (14 m/s)² / 2 x 9.8 m/s² = 10 m (Em relação ao telhado)

H_Máx = 10 m + 18 m = 28 m (Em relação à calçada).

b) para encontrar o Tempo total qualquer hora do voo durando no ar, a bola será usada a equação y = y_qualquer + v_qualquer.T - ½ g.t², Com os seguintes valores e sinais:

y = - 18 m

e_qualquer = 0 m

v_qualquer = +14 m/s

Substituindo:

- 18 = 14.T - ½ 9.8 .t²

- 4.9 t²+14.T + 18 = 0 

4.9 t²-14.T - 18 = 0

É uma equação de segunda graus que é facilmente resolvida com a ajuda de uma calculadora científica ou usando a resolução. As soluções são: 3.82 e -0.96. A solução negativa é descartada, pois é um momento em que falta significado físico.

Pode servir a você: calor: fórmulas e unidades, características, como é medido, exemplos

O tempo de vôo da bola é 3.82 segundos.

Exemplo 2 resolvido 2

Uma partícula carregada positivamente com Q = +1.2 milicoulombs (MC) e massa M = 2.3 x 10 ^-10 Kg É projetado verticalmente para cima, a partir da posição mostrada na figura e com velocidade inicial v_qualquer = 30 km/s.

Entre as placas carregadas, há um campo elétrico E uniforme, direcionado verticalmente para baixo e magnitude de 780 n/c. Se a distância entre as placas for de 18 cm, a partícula colidirá com a placa superior? Despreze a atração gravitacional na partícula, pois é extremamente leve.

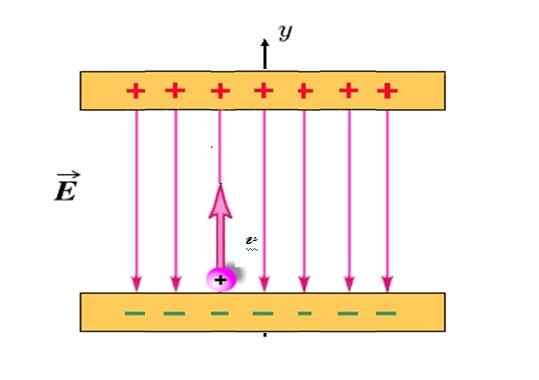Figura 4. Uma partícula de carga positiva se move semelhante a uma bola jogada verticalmente para cima, quando está imerso no campo elétrico da figura. Fonte: modificado por f. Sapato da Wikimedia Commons.

Solução

Neste problema, o campo elétrico E é aquele que produz uma força F e a conseqüente aceleração. Sendo carregado positivamente, a partícula é sempre atraída para a placa inferior, no entanto, quando for projetada verticalmente para cima, atingirá uma altura máxima e depois retornará à placa inferior, como a bola dos exemplos anteriores.

Por definição de campo elétrico:

E = f/q = m.A /q ⇒ a = q.E / m

É necessário usar essa equivalência antes de substituir os valores:

1 mc = 1 x 10^-3 C

Com isso, a aceleração é:

A = 1.2 x 10^-3 X 780 /2.3 x 10 ^-10EM² = 4.07 x 10⁹ EM²

Para a altura máxima, a fórmula da seção anterior é usada, mas em vez de usar “g"Esse valor de aceleração é usado:

e_Máx = v_qualquer² / 2a = (30.000 m/s)²/2 x 4.07 x 10⁹ EM² = 0.11 m = 11 cm

Não colida com a placa superior, pois é de 18 cm do ponto de partida, e a partícula assim que levanta 11 cm.

https: // youtu.Be/kt08ntudzwq

Referências

1. Kirkpatrick, l. 2007. Física: uma olhada no mundo. 6^ta Edição abreviada. Cengage Learning. 23 - 27.
2. Rex, a. 2011. Fundamentos da Física. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14^º. Ed. Volume 1. 50 - 53.
4. Serway, r., Vulle, c. 2011. Fundamentos da Física. 9^{n / D} Ed. Cengage Learning. 43 - 55.
5. Wilson, J. 2011. Física 10. Pearson Education. 133 - 149.