Tipos de triângulos

Classificação de triângulos

Um triângulo é um polígono ou figura geométrica que tem três lados, três vértices e três ângulos. Os lados são cada uma das linhas retas que a formam. Os vértices são os pontos em que os lados são unidos; Os ângulos são os arcos ou aberturas formadas perto dos vértices, juntando -se a dois lados.

Um triângulo também pode ser definido como a área determinada por três linhas. A soma de seus três ângulos é sempre igual a 180º. O comprimento de qualquer um de seus lados é sempre menor que o resultado da soma do comprimento dos outros dois lados, mas maior que sua subtração.

Os triângulos são as figuras geométricas mais simples e servem para investigar as propriedades matemáticas de outras figuras mais complexas, como pentágions ou hexágonos.

Eles também são usados ​​em outras ciências, como topografia, navegação ou astronomia. Neste último, eles são usados ​​para conhecer a distância que nos separa de um corpo azul claro distante de dois pontos de observação localizados na terra. Este método é conhecido como paralelagem.

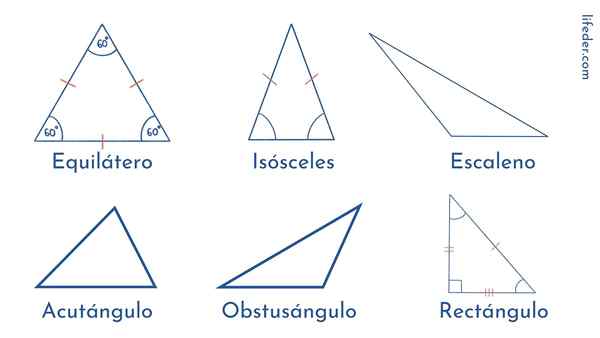
Os triângulos são classificados de acordo com a duração de seus lados ou de acordo com a amplitude de seus ângulos.

Tipos de triângulos de acordo com o lado deles

Triângulo equilátero

Os lados deste tipo de triângulo têm exatamente o mesmo comprimento. E o mesmo vale para seus ângulos: os três medidas 60º. É por isso que dizemos que o triângulo equilátero é um polígono comum.

Triângulo escaleno

Ao contrário do equilátero, no triângulo Scalene, tudo é desigual: seus três lados têm comprimentos diferentes e seus ângulos diferem na amplitude.

Pode atendê -lo: operações combinadas

Triângulo isósceles

Nesse tipo de triângulo, descobrimos que dois lados têm a mesma medida, enquanto o lado restante é diferente. O mesmo é observado na amplitude dos ângulos: dois são iguais e um diferente.

Tipos de triângulos de acordo com seus ângulos

Triângulo retângulo

É caracterizado por ter um ângulo reto, isto é, 90º. Seus outros dois ângulos são agudos ou menos de 90º.

Nesse tipo de triângulos, o lado mais longo é chamado hipotenusa, enquanto outros dois lados são as categorias.

Triângulo oblíquo

Triangles que não têm nenhum ângulo reto pertencem a este tipo. Eles são subdivididos em dois tipos:

Triângulo de Acutangle: Seus três ângulos são agudos.

Triângulo obtuso: Eles têm dois ângulos agudos e um obtusamente ou maior que 90º.

Triângulos mistos

O mesmo triângulo pode ser classificado de acordo com os dois critérios, isto é, de acordo com o comprimento de seus lados e a amplitude de seus ângulos.

Por exemplo, um triângulo retângulo também pode ser escalano ou isósceles, mas não poderia ser equilateral, pois o último não apresenta nenhum ângulo reto.

No entanto, um triângulo equilátero pode ser agudo, porque efetivamente tem três ângulos agudos ou menos de 90º.

Triângulo obtuso de Scalene

Um triângulo scaleno pode ser obtusamente, uma vez que a amplitude de seus ângulos e o comprimento de seus lados são diferentes.

Como calcular o perímetro de um triângulo?

O produto da soma do comprimento dos três lados de um triângulo é chamado de perímetro.

Vejamos alguns exemplos.

1- somos convidados a encontrar o perímetro de um triângulo Scaleno cujos lados 6, 8 e 4 centímetros. Tudo o que precisamos fazer é acrescentar:

Pode atendê -lo: constante absoluta

6 + 8 + 4 = 18

Portanto, o perímetro deste triângulo escaleno é de 10 centímetros.

2- Então eles nos pedem para calcular o perímetro de um triângulo de isósceles cujos lados medem 4 centímetros os dois e 6 centímetros do lado restante. Como dois de seus lados têm o mesmo comprimento, devemos colocar a mesma figura duas vezes, assim:

4 + 4 + 6 = 14

O perímetro deste triângulo é de 14 centímetros.

3- Um último exemplo. Temos a tarefa de determinar o perímetro de um triângulo equilátero de 9 centímetros de lado. Como conhecemos as características dos vários tipos de triângulos, sabemos que o equilátero é distinguido porque seus três lados são iguais. Portanto:

9 + 9 + 9 = 27

O perímetro deste equilíbrio é de 27 centímetros.

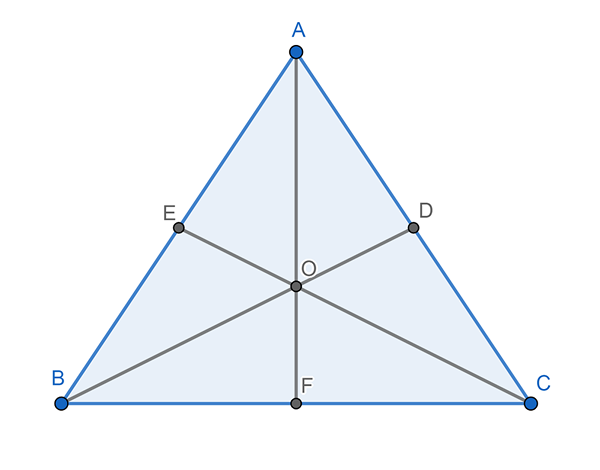
Mediatrices, bissetores e médios

Estes são os três tipos de linhas retas que podem ser desenhadas em um triângulo.

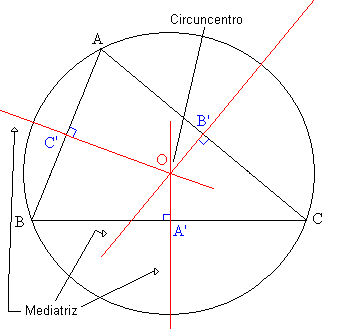
Mediatrices

Existem três, um de cada lado do triângulo. O MediaTrix é uma linha reta que passa pelo ponto médio do lado do triângulo para o qual corresponde. Os três mediatrices de um triângulo se cruzam em um ponto conhecido como circunncentro, que está na mesma distância de cada um dos vértices do triângulo.

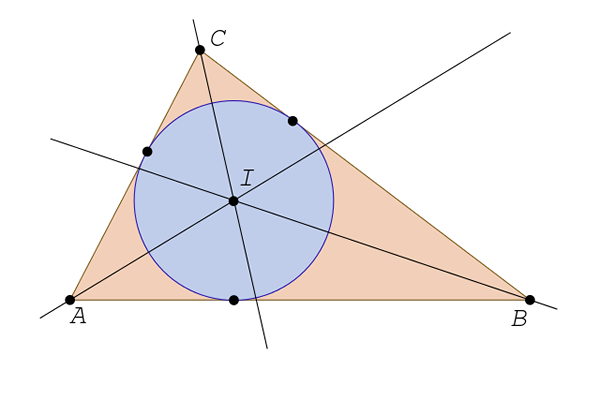
Bisectores

Existem três, um para cada ângulo. A bissetor é uma linha reta que começa no vértice e divide o ângulo em duas partes iguais. Os bissetores de um triângulo se cruzam em um ponto conhecido como incentivo.

Médio

Há também três, um para cada vértice. Uma mediana é uma linha que começa de um vértice e atinge o ponto médio do lado oposto. Os medianos de um triângulo se cruzam em um ponto chamado Baricentro.

Pode servir a você: Erro de amostragem: fórmulas e equações, cálculo, exemplos

A distância entre qualquer um dos três vértices e o baricentro é equivalente a dois terços (2/3) do comprimento total da mediana correspondente. Por exemplo, se a mediana CE mede 5 centímetros, a distância entre C e o baricenter (O) é igual a 5 x 2/3, ou o que é o mesmo, 5 x 0,66, o que resulta em 3, 3 centímetros.

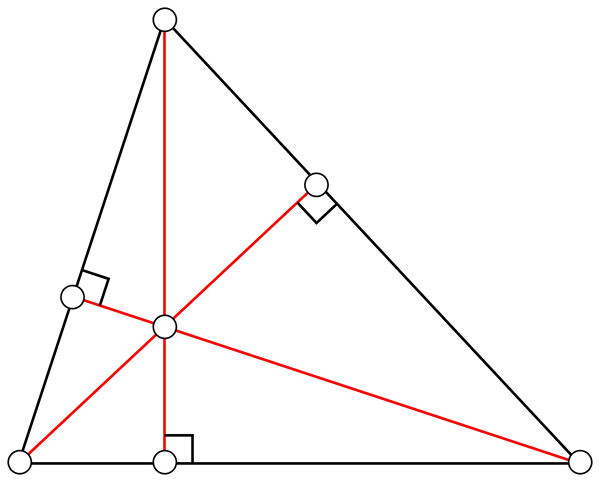
Alturas

É uma linha reta que se junta a um vértice com o lado oposto. As três alturas de um triângulo se cruzam em um ponto chamado Ortotroenter. Dependendo do tipo de triângulo, o ortocentro pode estar dentro ou fora da área do triângulo.

Como calcular a área do triângulo?

A área de um triângulo de qualquer tipo pode ser conhecida ao aplicar a seguinte fórmula:

A = b x h / 2

Nesta equação, a refere -se à área; B refere -se à base e H é a altura.

Vejamos um exemplo. Somos solicitados a calcular a área de um triângulo cuja base mede 12 centímetros e cuja altura é de 7 centímetros. Assim, temos:

B = 12

H = 7

Aplicamos a fórmula:

A = 12 x 7/2

A = 84/2

A = 44

Este triângulo, portanto, possui uma área de 44 centímetros quadrados.