Tetradecágono

O que é um tetradecágono?

O tetradecágono é uma figura geométrica plana e fechada de 14 lados, pertencentes à família Polgons. Também é conhecido pelo nome de tetrakaidecágono, Todas as palavras derivadas das palavras gregas: "tetra" (Cuatri), "kai" (mais), "decaimento" (dez) e "gon" (ângulo), pois também possui 14 ângulos internos.

A figura mostra um tetradagon regular, ou seja, cujos lados e ângulos internos têm a mesma medida, mostrando as principais características desta figura.

figura 1.- Tetrade regular com suas principais características. Fonte: f. Zapata.

Elementos tetradecágono

• Lados: Eles são chamados de 14 segmentos de linha que estão fechados para formar a figura. Todos eles podem ter o mesmo comprimento, nesse caso, o polígono é regular, ou pode ser diferente e depois há um tetrade irregular.
• Vértices: Eles são os pontos de interseção entre segmentos sucessivos e o tetradecágono tem 14 vértices.
• Centro: Ponto equidistante dos vértices.
• Rádio: segmento que une o centro com um vértice.
• Ângulo interno: É formado pelo interior da figura e entre dois segmentos sucessivos ou adjacentes. Mede 154.286º para o tetradecágon comum, independentemente do tamanho do lado.
• Ângulo externo: formado entre um lado e o prolongamento de um dos lados adjacentes. Independentemente do comprimento lateral, este ângulo mede 25.7143º para um tetrade comum.
• Ângulo central: Aquele que tem seu vértice coincidindo com o centro do polígono e seus lados são dois rádios consecutivos.
• Diagonal: segmento que conecta dois vértices não consecutivos.

Como é um tetradecágono?

Os polígonos regulares de n lados que são construídos com regra e bússola têm um n do formulário 2^r p₁… P_k, sendo p_Yo Números primo de Fermat, e por sua vez os números primos de Fermat tomam forma 2ⁿ + 1.

Pode atendê -lo: pendente de uma linha: fórmula e equações, representação, exemplos

O tetradecágono tem n = 14 lados, mas 14 = 7 × 2, que não são primos fermat, porque eles não podem ser expressos da maneira indicada. Portanto, este polígono não admite a construção exata com regra e bússola, mas uma construção que se aproxima muito bem, através de vários métodos.

Método geral para construir polígonos regulares

A seguir, é apresentado um método geral (não o único) a construir polígonos regulares registrados em uma circunferência, incluindo o tetrade comum.

Consiste em dividir o diâmetro vertical dessa circunferência em tantas partes iguais quanto os lados tem o polígono para desenhar. No caso de tetradecágono, eles serão as 14 partes numeradas na imagem 2. Estas são as etapas:

• Desenhe um diâmetro vertical de A a B.
• Em seguida, desenhe um semi -direito a partir do ponto A, abra a bússola com abertura arbitrária e faça 14 divisões igualmente espaçadas sobre isso. Semirreto e suas divisões podem sair da circunferência.
• Junte -se à marca 14VA (em azul na imagem) no final do semi -direito com o ponto B.
• Para continuar se juntando ao restante das marcas no semi -recreação com os respectivos pontos no diâmetro vertical (pontos verdes).
• Com a ponta da bússola em A e a abertura igual à medida do diâmetro da circunferência, um arco é desenhado. Com a mesma medida, mas apoiando a ponta em B (ponto 14 da Figura 2), é desenhado outro arco, que é cortado com o primeiro nos pontos V e V 'indicado.

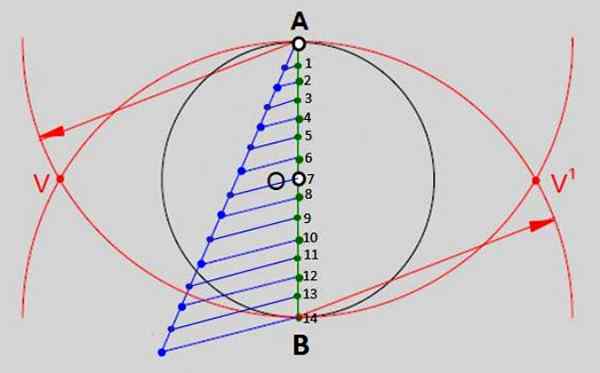Figura 2.- Um dos métodos gerais para construir polígonos regulares é dividir o diâmetro da circunferência em tantas partes iguais quanto os lados tem o polígono. No caso de tetradech regulares, existem 14 partes iguais. Fonte: f. Zapata.

• Agora, com a regra, desenhe uma linha de v 'para o ponto 2 e prolongue -a para cruzar a circunferência no ponto C da Figura 3. Marque o ponto de interseção, que será um dos vértices da figura.

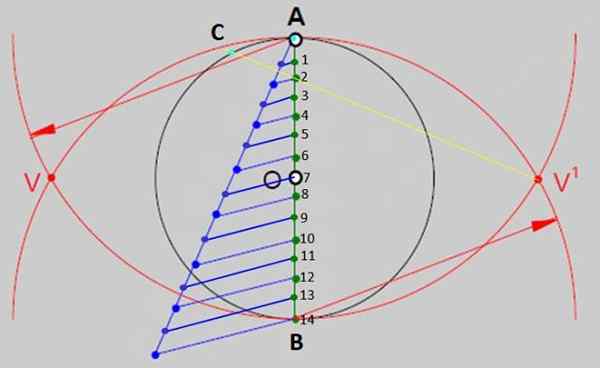Pode atendê -lo: ramificações de estatísticas Figura 3.- O segmento AC é a medida dos lados da tetradecion construída. Fonte: f. Zapata.

• Abra a bússola na distância CA e apoiando a ponta em A ou C, desenhando arcos de igual medida em toda a circunferência, dessa maneira é dividida em partes aproximadamente iguais, as interseções entre os arcos e a circunferência são os vértices são os vértices de tetradecágono.
• Com uma regra, junte -se aos vértices com segmentos de linha, formando os lados do polígono.
• Apagar cuidadosamente construções auxiliares.

Na animação seguinte, é mostrado outro método aproximado, com regra e bússola:

Figura 4.- Animação que mostra como um tetradecágon é feito (polígono aproximadamente regular). Fonte: Wikimedia Commons.

Fórmulas para tetrade regular

As fórmulas a seguir são válidas para polígonos regulares:

• Número da folha: n
• Medida lateral: A
• Apothem: l_PARA
• Rádio: r
• Perímetro: p
• Área: a
• Ângulo interno: eu
• Ângulo externo: e
• Diagonal: d

Lado conhecido do apotem

A = 2L_PARA × TG (π/n)

Para n = 14:

A = 2L_PARA × TG (π/14)

Lado conhecido o rádio

A = 2r × sen (π/n)

Sim n = 14:

A = 2r × sen (π/14)

Perímetro conhecido do lado

O perímetro é a soma dos lados. Quando o tetradecágono é regular:

P = n⋅a = 14⋅A

Se o tetradecágono for irregular, todos os lados devem ser adicionados diretamente para obter o perímetro.

Área conhecida do lado

A = ¼ na² × berço (π/n)

Para n = 14:

A = ¼ (14º²) × berço (π/14) = (7/2) A² × berço (π/14)

Área conhecida

A = n⋅l_PARA ² × TG (π/n)

Tomando n = 14 resultados:

A = 14L_PARA ² × TG (π/14)

Área baseada no perímetro e apothem

A = (p × l_PARA)/2

Pode servir você: Teorema de Bayes

Medida do ângulo interno

 Quando n = 14, o ângulo interno das medidas de tetradecágono em graus:

I = 12 × 180º /14 = 154.286º

Medição de ângulo externo

E = 360º/n

Quando n = 14 você tem:

E = 25.7143º

Diagonais

A fórmula para calcular o número de diagonais presentes em qualquer polígono, regular ou não, é:

Para n = 14:

D = 14 × 11/2 = 77 diagonais

Exemplos

Outro exemplo de tetradecágon

Os polígonos regulares aparecem repetidamente em vários projetos, como moedas. No caso de tetradagon regular, isso aparece em moedas comemorativas da Malásia, representando seus lados de cada um dos quatorze estados confederados daquela nação.

Côncavo e convexo tetradecágonos

Em geral, polígonos como tetradecágono podem ser convexos ou côncavos, no primeiro caso, a medida de seus ângulos internos não excede 180º. A tetradech regular é convexa, como qualquer polígono regular, já que qualquer um de seus ângulos internos mede 154.286º.

Por outro lado, na tetradech côncava, um ou mais de seus ângulos internos mede mais de 180º.

Exemplo numérico

Dado um tetradagon regular cujo lado mede 5 cm, encontre:

a) perímetro
b) Medição de apotemas
c) comprimento do rádio
d) Área

Respostas

a) Como é um polígono regular, o perímetro é:

P = 14 × 5 cm = 70 cm.

b) da Equação A = 2L_PARA × tg (π/14), onde a = 5 cm, o apothem L_PARA:

eu_PARA = a / [2 × Tg (π / 14)] = 5 cm / 0.4565 = 21.9064 cm

c) O rádio r pode ser calculado por a = 2r × sen (π/14):

R = a / [2 × sin (π / 14)] = 5 cm / 0.4565 = 22.4698 cm

d) Existem várias alternativas para a área, por exemplo A = (p × L_PARA)/2:

A = (70 × 21.9064)/2 cm² = 1533.45 cm².

Referências

1. Alexander, d. 2013. Geometria. 5 ª. Edição. Cengage Learning.
2. Geometria de Arturo. Método geral para desenhar polígonos inscritos em circunferências. Recuperado do YouTube.com
3. Calculadora de sopa. Calculadora regular de polígonos. Recuperado de: calculatorosoup.com.
4. Desenho. Polígonos regulares. Recuperado de: desenho.com.
5. Requena, b. Polígono côncavo. Recuperado de: universoformulas.com.
6. Wikipedia. Polígono Buildível. Recuperado de: é.Wikipedia.org.