Característica de teselados, tipos (regulares, irregulares), exemplos

O Tesselled São superfícies cobertas por uma ou mais números chamados Tessels. Eles estão por toda parte: em ruas e edifícios de todos os tipos. Tessels ou azulejos são peças planas, geralmente polígonos com cópias congruentes ou isométricas, que são colocadas seguindo um padrão regular. Dessa maneira, não há espaços sem serem cobertos e os azulejos ou mosaicos não se sobrepõem. 

No caso de um único tipo de mosaico formado por um polígono comum é usado, então há um Tesseld regular, Mas se dois ou mais tipos de polígonos regulares são usados, então é um Tessell semi -regular.

figura 1. Piso de ladrilho irregular, porque os retângulos são polígonos não regulares, mesmo quando os quadrados são. Fonte: Pixabay.

Finalmente, quando os polígonos que formam o tesseldo não são regulares, então é um Tesselled irregular.

O tipo mais comum de tesseldo é o formado por mosaicos retangulares e particularmente quadrados. Na Figura 1, temos um bom exemplo.

[TOC]

História dos Teselados

O Tessellation tem sido usado há milhares de anos para cobrir pisos e paredes de palácios e templos de diferentes culturas e religiões.

Por exemplo, a civilização suméria que floresceu em torno de 3500 para.C. Ao sul da Mesopotâmia, entre os rios Eufrates e Tigre, eles usaram os tesels em sua arquitetura.

Figura 2. Teselados Sumerios na porta de Istar. Fonte: Wikimedia Commons.

Os tesels também despertaram o interesse dos matemáticos de todos os tempos: começando com arquimedes no terceiro século aC, seguido por Johannes Kepler em 1619, Camille Jordan em 1880, até os tempos contemporâneos com Roger Penrose.

Pode servir a você: Fração equivalente a 3/5 (solução e explicação)

Penrose criou uma teselação não periódica conhecida como Penrose Tessellation. Eesses São apenas alguns nomes de cientistas que contribuíram muito sobre tesellation.

Tesels regulares

Teslate regular é feito com um único tipo de polígono comum. Por outro lado, para que o Tesseldo possa ser considerado regular todo o ponto do avião deve:

-Pertencem ao interior do polígono

-Ou à beira de dois polígonos adjacentes 

-Finalmente, pode pertencer ao vértice comum de pelo menos três polígonos.

Com as restrições acima, pode -se demonstrar que apenas os triângulos equiláteis, os quadrados e os hexágonos podem formar um tessel comum.

Nomenclatura

Há uma nomenclatura para denotar os tesels que consistem na listagem na direção das agulhas do relógio e separados por um ponto, o número de lados dos polígonos que cercam cada nó (ou vértice) do tesellled, sempre começando com o menor número de lados.

Esta nomenclatura se aplica a tesselves regulares e semi -regulares. 

Exemplo 1: Teselado triangular

A Figura 3 mostra um ladrilho regular triangular. Deve -se notar que cada nó de ladrilho triangular é o vértice comum de seis triângulos equiláteis. 

A maneira de denotar esse tipo de tesseldo é 3.3.3.3.3.3, que também é denotado por 3⁶.

Figura 3. Teselado regular triangular 3.3.3.3.3.3. Fonte: Wikimedia Commons

Exemplo 2: Tessel quadrado

A Figura 4 mostra um ladrilho regular composto apenas de quadrados. Deve -se notar que cada nó de ladrilho está cercado por quatro quadrados congruentes. A notação que se aplica a esse tipo de tesselves quadrados é: 4.4.4.4 o alternadamente 4⁴

Figura 4. Tesseld quadrado 4.4.4.4. Fonte: Wikimedia Commons.

Exemplo 3: Tesseld hexagonal

Em uma tesselle hexagonal. A nomenclatura para uma brecha hexagonal regular é 6.6.6 o alternadamente 6³.

Pode servir a você: seções cônicas: tipos, aplicações, exemplos Figura 5. Tesseld hexagonal 6.6.6. Fonte: Wikimedia Commons.

Tessell semi -regular

Tesels de arquimedes semi -regular ou tessel consiste em dois ou mais tipos de polígonos regulares. Cada nó é cercado pelos tipos de polígonos que compõem o tesselado na mesma ordem e a condição de uma borda completamente compartilhada com o vizinho é mantida.

Existem oito tesels semi -regulares:

1. 3.6.3.6 (Tri-hexagonal Tesselled)
2. 3.3.3.3.6 (Texagonal Teslate Romo)
3. 3.3.3.4.4 (teselado triangular de Elongado)
4. 3.3.4.3.4 (Romo Square Tesselled)
5. 3.4.6.4 (Rombi-tri-hexagonal Tesseld)
6. 4.8.8 (quadrado truncado Tesselled)
7. 3.12.12 (Tesseld hexagonal truncado)
8. 4.6.12 (Tesseld truncado tri-hexagonal)

Alguns exemplos de teslato semi -regular são mostrados abaixo.

Exemplo 4: Tixagonal Teselado

É o que é composto por triângulos equilaterais regulares na estrutura 3.6.3.6, o que significa que um nó de ladrilho está cercado (até completar um retorno) por um triângulo, um hexágono, um triângulo e um hexágono. A Figura 6 mostra uma tessel.

Figura 6. Tesseld tri-hexagonal (3.6.3.6) É um exemplo de bico semi -regular. Fonte: Wikimedia Commons.

Exemplo 5: Hexagonal Tesseldo Romo

Como o ladrilho do exemplo anterior, isso também consiste em triângulos e hexágonos, mas sua distribuição em torno de um nó é 3.3.3.3.6. A Figura 7 ilustra claramente esse tipo de tesselled.

Figura 7. O Tesseldo Romo hexagonal consiste em um hexágono cercado por 16 triângulos na configuração 3.3.3.3.6. Fonte: Wikimedia Commons.

Exemplo 6: Tessel de Rombi-tri-hexagonal

É um ladrilho que consiste em triângulos, quadrados e hexágonos, na configuração 3.4.6.4, que é mostrado na Figura 8.

Figura 8. Tessell semi -regular composto por um triângulo, um quadrado e um hexágono na configuração 3.4.6.4. Fonte: Wikimedia Commons.

Tesels irregulares

Eles são chamados tesels irregulares para aqueles que são formados por polígonos irregulares ou por polígonos regulares, mas que não cumprem o critério de que um nó é um vértice de pelo menos três polígonos.

Pode servir a você: Antiderivativo: fórmulas e equações, exemplos, exercícios

Exemplo 7

A Figura 9 mostra um exemplo de azulejo irregular, no qual todos os polígonos são regulares e congruentes. É irregular porque um nó não é um vértice comum de pelo menos três quadrados e também há quadrados vizinhos que não compartilham completamente uma vantagem.

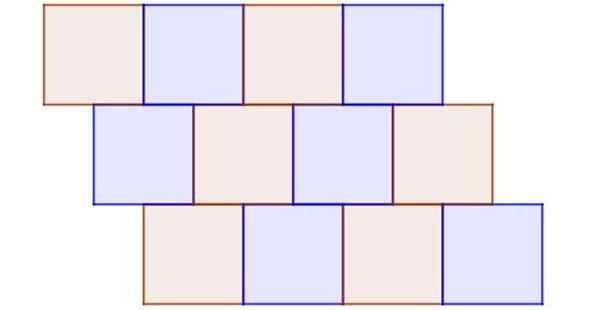Figura 9. Mesmo quando todos os ladrilhos são quadrados congruentes, este é um exemplo claro de tessel de forma irregular. Fonte: f. Zapata.

Exemplo 8

O paralelogramo camisa uma superfície plana, mas, a menos que seja um quadrado, não pode formar um tessel comum.

Figura 10. Um tesseldo formado por paralelogramas é irregular, pois seus mosaicos são polígonos não -regulares. Fonte: f. Zapata.

Exemplo 9

Hexágonos não regulares com simetria central define uma superfície plana, como mostrado na figura a seguir:

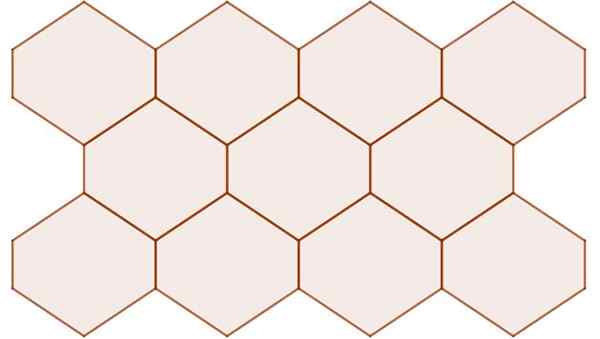Figura 11. Hexágonos com simetria central, mesmo quando não são regulares, eles definem o avião. Fonte: f. Zapata.

Exemplo 10: El Cairo Teselado

É uma teselação muito interessante, composta de pentágio.

Chega o nome dele que este Tesseld está na calçada de algumas das ruas do Cairo no Egito. A Figura 12 mostra o Tesseldo do Cairo.

Figura 12. Cairo Tesseldo. Fonte: Wikimedia Commons.

Exemplo 11: Teselado al-Andalus

Tesseldo durante algumas partes da Andaluzia e Norte da África são caracterizados por geometria e epigrafia, além de elementos ornamentais como a vegetação. 

Palacios de Tessell, como o Alhambra, composto por ladrilhos formados por pedaços de cerâmica de muitas cores, com formas múltiplas (para não dizer infinitas) que desencadeavam gráficos geométricos.

Figura 13. Teselado Palacio de la Alhambra. Tartaglia / domínio público

Exemplo 12: Teselado nos videogos

Também conhecido como tesellation, é um dos mais boom nos videogames. Esta é a criação de texturas para simular o tesseld dos diferentes cenários que aparecem no simulador.

Esta é a reflexão clara de que essas capas continuam a evoluir transferindo as fronteiras da realidade.

Referências

1. Desfrute de matemática. Tesels. Recuperado de: desfrutar.com
2. Rubiños. Tesels resolveu exemplos. Recuperado de: matemática.Blogspot.com
3. Weisstein, Eric W. "Deiregula Tessellation". Weisstein, Eric W, Ed. Mathworld. Pesquisa de Wolfram.
4. Wikipedia. Tesselled. Recuperado de: é.Wikipedia.com
5. Wikipedia. Tesseld regular. Recuperado de: é.Wikipedia.com