Miletus como o teorema

Explicamos o primeiro e o segundo teorema de tais, com exemplos e exercícios resolvidos

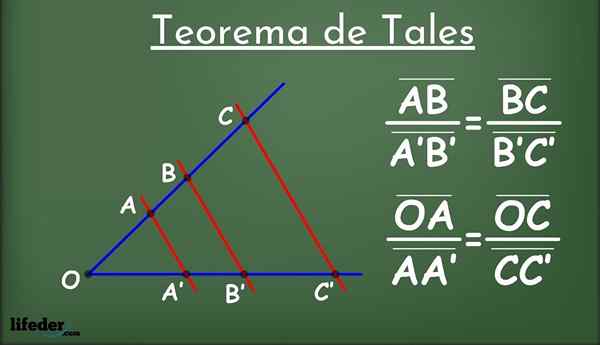
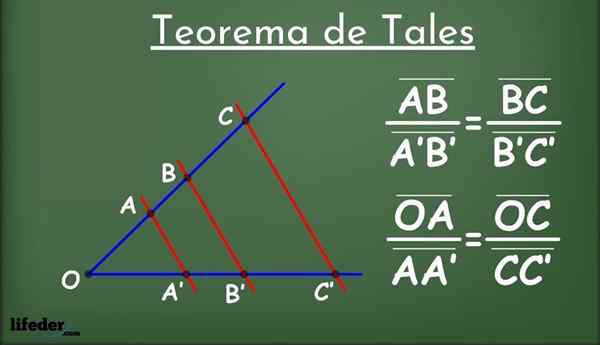figura 1.- The Tales Teorema

O que é tal?

Ele Tal teorema De Miletus, ele realmente se refere a vários teoremas de geometria atribuídos aos sábios da antiga Grécia Thales de Miletus, que viveu de 624 a 546 ac em Miletus, Turquia atual.

Além de matemático e geômetro, esse era um filósofo reconhecido por sua grande nitidez. Dizem que ele conseguiu medir a altura da Grande Pirâmide através do uso de um de seus teoremas.

Ele Primeiro teorema de tal Refere -se aos segmentos que um grupo de linhas paralelas determina em duas linhas no plano. Esses segmentos mantêm uma proporção de proporcionalidade, como será visto em breve, que é estendido para os lados de dois triângulos, desde que certas condições sejam atendidas.

Este teorema é extremamente útil na prática, pois permite determinar a altura de estruturas muito altas ou difíceis de acessar, sem a necessidade de medi -las diretamente. Foi exatamente isso que os contos fizeram quando ele mediu a altura da Grande Pirâmide.

Por sua parte, o Segundo teorema deste Pontos de link que pertencem a uma circunferência com um triângulo retângulo registrado nele, cuja hipotenusa coincide com seu diâmetro.

Primeiro teorema de tal

Ser duas linhas em um avião, chamado L₁ e eu₂ (em azul na Figura 1) e um grupo de linhas paralelas entre si (em vermelho) que se cruzam l₁ e eu₂.

As linhas paralelas dividem as linhas em segmentos L₁ e eu₂: Ab, a'b ', bc, b'c' e assim por diante. Entre os segmentos enfrentados, a seguinte relação proporcionalidade é estabelecida:

Por exemplo, nesta figura, a medida do segmento "x" é calculada pelo teorema de tal, uma vez que as linhas são intercebidas por vários paralelos que determinam segmentos com comprimento conhecido:

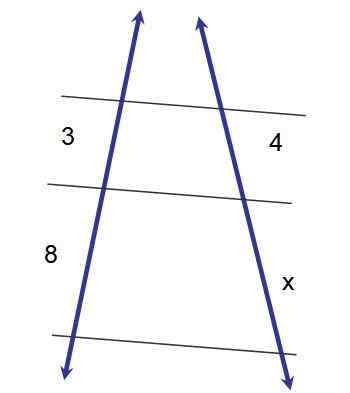Pode atendê -lo: eventos mutuamente exclusivos: propriedades e exemplosFigura 2.- Aplicação do primeiro teorema desse tipo para determinar a medida do segmento x. Fonte: f. Zapata.

3x = 32

x = 32/3 ≈ 10.7

O teorema desse tipo para triângulos semelhantes

O teorema pode ser estendido aos triângulos da seguinte forma: Suponha que haja um triângulo ABC no qual um segmento paralelo é atraído por um de seus lados. Dessa maneira, dois triângulos semelhantes são obtidos: ABC e DEC, cujos ângulos internos são congruentes, ou seja, eles têm igual medida.

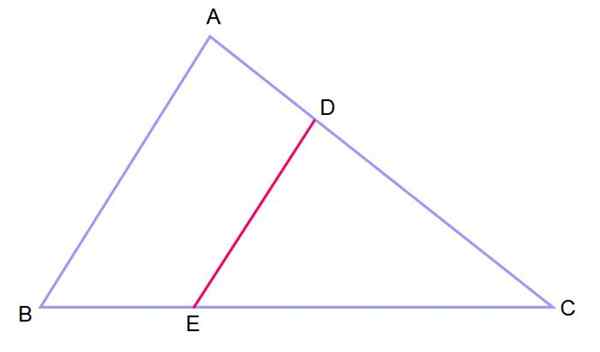Figura 3.- Dois triângulos na posição de tal, com dois lados paralelos e um ângulo comum, são semelhantes. Fonte: f. Zapata.

Quando você tem dois triângulos organizados dessa maneira, diz -se que eles estão em tal posição.

Uma proporção de proporcionalidade entre os segmentos é aumentada da mesma maneira que para as linhas paralelas:

Que é equivalente a esse outro, entre os lados correspondentes de cada triângulo, também chamados de lados homólogos:

Cada um desses quocientes é chamado razão de similaridade. Em triângulos semelhantes, o motivo da similaridade é igual ao quociente entre os perímetros e o quadrado da razão de similaridade é igual ao quociente entre as áreas.

Em seguida, um exemplo em que o teorema desse tipo pode ser aplicado a triângulos semelhantes e descobrir quanto vale o lado desconhecido x.

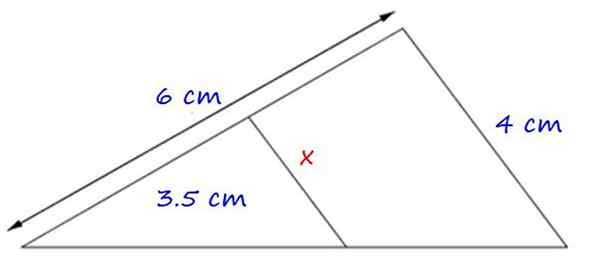Figura 4.- Exemplo de aplicação do primeiro teorema desse tipo. Fonte: f. Zapata.

Os triângulos formados são semelhantes, pois têm um ângulo comum e os lados x e 4 cm são paralelos.

Portanto, a proporcionalidade entre os lados correspondentes é:

E o valor de x é facilmente limpo:

x = (4 × 3.5) ÷ 6 cm = 2.3 cm

Segundo teorema deste

Este teorema se refere a um triângulo cujos vértices são pontos que pertencem a uma circunferência, o que significa que está registrado nele.

Nesse caso, o teorema estabelece que sempre que o hipotenusa corresponde ao diâmetro da circunferência, o triângulo assim rastreado é retângulo, ou seja, um de seus ângulos internos mede 90º, como visto na Figura 5 à esquerda.

Pode atendê -lo: simbolização de expressões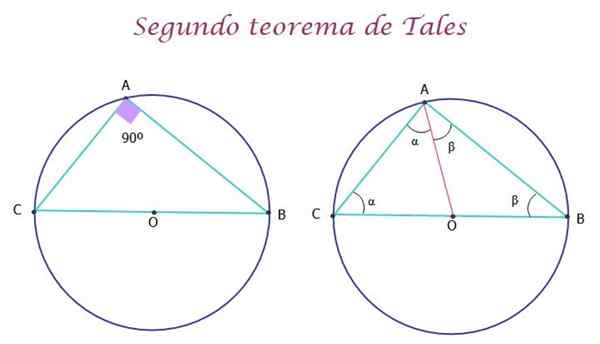Figura 5.- O segundo teorema de tais estados que o triângulo registrado na circunferência é retângulo. Fonte: f. Zapata.

Demonstração do segundo teorema de tal

A demonstração do teorema é muito simples. Na figura acima, o segmento AO foi desenhado em vermelho, para formar os dois triângulos AOC e AOB, que são isósceles, já que os lados OA, OC e OB são rádios das circunferências e, portanto, medem o mesmo.

Dessa forma, os triângulos têm dois ângulos iguais, que são respectivamente α e β. Agora, para o triângulo ABC original, como para qualquer triângulo, é cumprido que a soma das medidas de seus ângulos internos é igual a 180º, portanto:

α + (α + β) + β = 180º

Por isso:

2α + 2β = 180º

Portanto:

2 (α +β) = 180º

α +β = 90º

Que prova que o triângulo ABC tem um ângulo interno de 90º e, portanto, é um triângulo certo.

Exemplo

Na figura seguinte, o triângulo ABC é isósceles e retângulo (triângulo de Isorectangle), sendo o perímetro da circunferência igual a 25 cm. Quanto são os segmentos AC e AB?

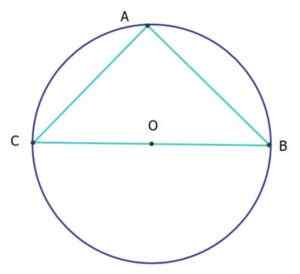
O perímetro da circunferência é o seu comprimento l, dado dependendo do seu diâmetro d pela fórmula:

L = πd

Portanto, o diâmetro, que é o segmento CB, mede:

D = cb = l/ π = 25 cm/ π = 7.96 cm.

Como o triângulo é isósceles, isso significa que seus ângulos agudos medem 45º cada. Como a hipotenusa do triângulo é o diâmetro da circunferência, uma proporção trigonométrica de 45 pode ser usada, por exemplo:

Sen 45º = AC/CB

AC = CB × Sin 45º = 7.96 cm × sin 45º = 5.64 cm

Pode servir você: Teorema de Moivre

O lado AB tem a mesma medida: 5.64 cm, já que o triângulo é isósceles.

Tais aplicativos de teorema

O primeiro teorema desse tipo pode ser usado para conhecer distâncias que não são facilmente mensuráveis. Dizem que tal viajou para o Egito e para lá determinado, de uma maneira muito engenhosa, a altura da Grande Pirâmide.

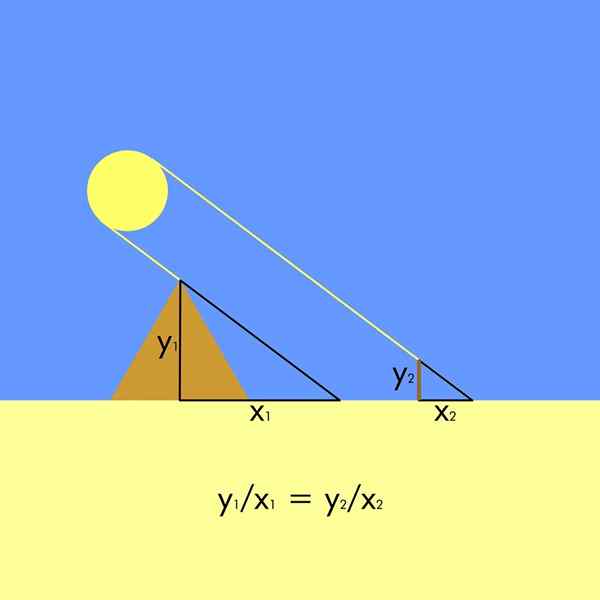
Para isso, era necessário. Assim, dois triângulos semelhantes são formados, uma vez que os raios do sol têm incidência paralela.

Na figura, a altura da pirâmide é e₁ E sua sombra é x₁, Enquanto a altura da estaca é e₂ (Alguns cronistas afirmam que tal usavam sua própria altura) e sua sombra é x₂. Como os triângulos são semelhantes, é formada a seguinte relação proporcionalidade:

Sendo muito fácil de limpar a altura da pirâmide e₁:

e₁ = x₁∙ (e₂ ÷ x₂)

Referências

1. Alexander, d. 2013. Geometria. 5 ª. Edição. Cengage Learning.
2. Requena, b. Tal teorema. Recuperado de: universoformulas.com.
3. Salão matemático. Tales de Mileto e a Grande Pirâmide. Recuperado de: salonmatematic.com
4. Material didático superprofito. Miletus como. Recuperado de: superprof.é.
5. Teorema de Thales e semelhança. Dois problemas muito antigos. Recuperado de: edu.Xunta.Garota.