Exemplos de sucessões quadráticas, regra e exercícios resolvidos

As Sucessões quadráticas, Em termos matemáticos, eles consistem em sequências de números que seguem uma certa regra aritmética. É interessante conhecer esta regra para determinar qualquer um dos termos de uma sucessão.

Uma maneira de conseguir isso é determinar a diferença entre dois termos sucessivos e ver se o valor obtido é sempre repetido. Quando assim, diz -se que é um Sucessão regular.

Sucessões numéricas são uma maneira de organizar sequências de números. Fonte: Pixabay.com

Mas se não for repetido, você pode tentar examinar o diferença entre diferenças E veja se esse valor é constante. Se sim, então é um Sucessão quadrática. 

[TOC]

Exemplos de sucessões regulares e sucessões quadráticas

Os exemplos a seguir ajudam a esclarecer o que foi explicado até agora:

Exemplo de sucessão regular

Seja a sucessão s = 4, 7, 10, 13, 16, ...

Esta sucessão, indicada por S, é um conjunto numérico infinito, neste caso de números inteiros.

Pode -se observar que é uma sucessão regular, porque cada termo é obtido adicionando 3 ao termo ou elemento anterior:

4

4 +3 = 7

7+3 = 10

10+3 = 13

13+3 = 16

Em outras palavras: esta sucessão é regular porque a diferença entre o termo seguinte e a anterior fornece um valor fixo. No exemplo, dado este valor é 3.

As sucessões regulares obtidas adicionando uma quantia fixa ao termo anterior também são chamadas progressões aritméticas. E para a diferença - constante - entre termos sucessivos, é chamado razão E é denotado como r.

Exemplo de sucessão não -regular e quadrática

Veja agora a seguinte sucessão:

S = 2, 6, 12, 20, 30, .. .

Quando as diferenças sucessivas são calculadas, os seguintes valores são obtidos:

Pode atendê -lo: seleções aleatórias com ou sem substituição

6-2 = 4

12-6 = 6

20-12 = 8

30-20 = 10

Suas diferenças não são constantes, então pode -se dizer que é uma sucessão não regulamentar.

No entanto, se considerarmos o conjunto de diferenças, há outra sucessão, que será denotada como S_Di:

S_Di = 4, 6, 8, 10, .. .

Esta nova sucessão é uma Sucessão regular, Como cada termo é obtido adicionando o valor fixo r = 2 ao anterior. É por isso que podemos afirmar que S é Sucessão quadrática.

Regra geral para construir uma sucessão quadrática

Há uma fórmula geral para construir uma sucessão quadrática:

T_n = A ∙ n² + B ∙ n +c

Nesta fórmula, t_n É o termo do n da sucessão. A, B e C são valores fixos, enquanto N varia um a um, ou seja, 1, 2, 3, 4, ..

Em sucessão s do exemplo anterior a = 1, b = 1 e c = 0. A partir daí, segue -se que a fórmula que gera todos os termos é: t_n = n² + n

Quer dizer:

T₁ = 1² + 1 = 2

T₂ = 2² + 2 = 6

T₃ = 3² + 3 = 12

T₅ = 5² + 5 = 30

T_n = n² + n

Diferença entre dois termos consecutivos de uma sucessão quadrática

T_N+1 - T_n = [A ∙ (n+1)² + B ∙ (n + 1) + c] - [a ∙ n n² + B ∙ n +c]

Desenvolver a expressão através de um produto notável permanece:

T_N+1 - T_n = A ∙ n² + A ∙ 2 ∙ n + a + b ∙ n + b + c - a ∙ n n² - B ∙ N - C

Simplificando -o: você recebe:

T_N+1 - T_n = 2 ∙ a ∙ n + a + b

Esta é a fórmula que dá a sucessão das diferenças s_Di que pode ser escrito assim:

Di_n = A ∙ (2n+1)+b

Onde claramente o termo a seguir é 2 ∙ às vezes o anterior. Isto é, a razão da sucessão das diferenças s_Di Es: r = 2 ∙ a.

Exercícios resolvidos de sucessões quadráticas

Exercício 1

Seja a sucessão s = 1, 3, 7, 13, 21,…. Determine sim:

i) é regular ou não

ii) é quadrático ou não

iii) foi quadrático, a sucessão de diferenças e sua razão

Pode atendê -lo: limitar as propriedades (com exemplos)

Respostas

i) Vamos calcular a diferença no termo seguinte e no anterior:

3-1 = 2

7-3 = 4

13-7 = 6

21-13 = 8

Podemos afirmar que a sucessão s não é regular, porque a diferença entre termos sucessivos não é constante.

ii) A sucessão das diferenças é regular, porque a diferença entre seus termos é o valor constante 2. Portanto, a sucessão original é quadrática.

iii) já determinamos que S é quadrático, a sucessão das diferenças é:

S_Di = 2, 4, 6, 8,… e sua razão é r = 2.

Exercício 2

Seja a sucessão s = 1, 3, 7, 13, 21,… do exemplo anterior, onde foi verificado que é quadrático. Determinar:

i) a fórmula que determina o termo geral t_{n .}

ii) Verifique o terceiro e o quinto termo.

iii) o valor do décimo termo.

Respostas

i) a fórmula geral de t_n é um ∙ n² + B ∙ n +c. Então se sabe os valores de A, B e C.

A sucessão de diferenças está certa 2. Além de qualquer sucessão quadrática, o motivo de r é 2 ∙ A, como demonstrado nas seções anteriores.

R = 2 ∙ a = 2 que nos leva a concluir que a = 1.

O primeiro mandato da sucessão de diferenças s_Di É 2 e deve cumprir em ∙ (2n+1)+b, com n = 1 e a = 1, ou seja:

2 = 1 ∙ (2 ∙ 1+1)+b

A limpeza B é obtida: B = -1

Então o primeiro termo de S (n = 1) Vale 1, ou seja: 1 = A ∙ 1² + B ∙ 1 + C. Como já sabemos que A = 1 e B = -1, substituindo -nos, nos resta:

1 = 1 ∙ 1² + (-1) ∙ 1 +c

A limpeza c é obtida seu valor: c = 1.

Em resumo:

A = 1, b = -1 e c = 1

Então o termo é apenas_n = n² - N + 1

ii) o terceiro termo t₃ = 3² - 3 + 1 = 7 e é verificado. O quinto t₅ = 5² - 5 + 1 = 21 que também é verificado.

iii) o décimo termo será t₁₀ = 10² - 10 + 1 = 91.

Exercício 3

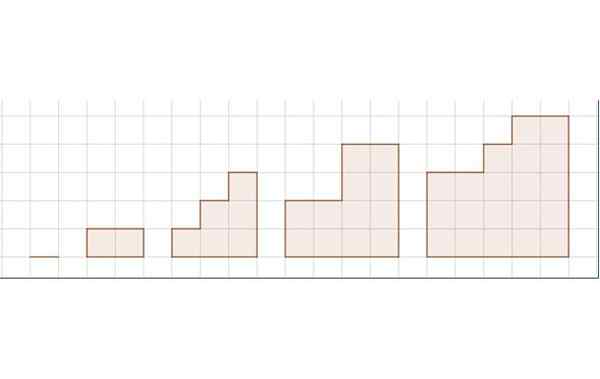Sequência de áreas para o Exercício 3. Fonte: Self feito.

A figura mostra uma sequência de cinco figuras. O reticulado representa a unidade de comprimento.

Pode atendê -lo: diferença entre uma fração comum e um número decimal

i) Determine a sucessão para a área de figuras.

i) Mostre que é uma sucessão quadrática.

iii) Encontre a área da Figura nº 10 (não mostrada).

Respostas

i) A sucessão correspondente à área da sequência de figuras é:

S = 0, 2, 6, 12, 20,…

ii) A sucessão correspondente às diferenças consecutivas dos termos de S é:

S_Di = 2, 4, 6, 8,…

Como as diferenças entre termos consecutivos não são constantes, então S não é uma sucessão regular. Deve saber se é quadrático, para o qual fazemos novamente a sequência das diferenças, obtendo:

2, 2, 2, .. .

Como todos os termos da sequência são repetidos, é confirmado que S é uma sucessão quadrática.

iii) sucessão_Di é regular e seu motivo R é 2. Usando a equação anteriormente demonstrada r = 2 ∙ a, permanece:

2 = 2 ∙ A, o que implica que a = 1.

O segundo termo da sucessão de diferenças s_Di É 4 e o n-EME de s_Di é

A ∙ (2n+1)+b.

O segundo termo tem n = 2. Também foi determinado que A = 1, portanto, usando a equação anterior e a substituição é:

4 = 1 ∙ (2 ∙ 2+1)+b

A limpeza B é obtida: B = -1.

Sabe -se que o segundo termo de S vale 2 e que a fórmula do termo geral deve cumprir com n = 2:

T_n = A ∙ n² + B ∙ n +c; n = 2; A = 1; B = -1; T₂ = 2

Quer dizer

2 = 1 ∙ 2² - 1 ∙ 2 + c

Conclui -se que C = 0, ou seja, a fórmula que dá ao termo geral da sucessão é:

T_n = 1 ∙ n² - 1 ∙ n +0 = n² - n

Agora o quinto termo é verificado:

T₅ = 5² - 5 = 20

iii) Figura 10, que não foi desenhada aqui, terá a área correspondente ao décimo termo da sucessão S:

T₁₀ = 10² - 10 = 90

Referências

1. https: // www.Geogebra.org