Sistema de coordenadas retangulares

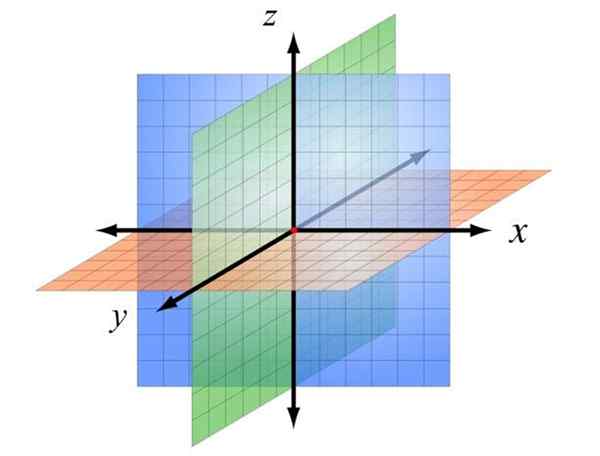
Sistema de coordenadas cartesianas em três dimensões. Fonte: Wikimedia Commons

Qual é o sistema de coordenadas retangulares?

Em matemática e geometria, um Sistema de coordenadas retangulares Serve para localizar com precisão qualquer ponto no espaço. Para isso, basta dar três coordenadas.

A construção do sistema no avião é muito simples, apenas três linhas que serão os eixos de coordenadas ou os eixos cartesianos são necessários: uma vertical, outra horizontal e um terceiro que entra ou deixa o papel ou a tela.

Esses eixos são mutuamente perpendiculares e o ponto de interseção é o origem do sistema.

Esta disposição é mostrada na figura acima, na qual as letras foram atribuídas às letras x, e, z, para distingui -los. Dessa maneira, três aviões são determinados, com a origem colorida em vermelho.

O plano Xz, Em azul, é o plano da tela e está na frente dos olhos do leitor. O plano XY É laranja e pode ser associado à mesa ou ao piso. Finalmente, o avião ZY Em verde, é perpendicular aos anteriores e a seção da tela ou papel em duas regiões.

Quadriculando cada um desses aviões e atribuindo uma escala, você pode colocar qualquer ponto no espaço, dando às respectivas coordenadas X e z, Sempre nessa ordem, para evitar ambiguidades.

Para queServe o sistema de coordenadas retangulares?

O sistema de coordenadas retangulares serve para posicionar qualquer ponto no espaço ou no avião, o suficiente para indicar as três coordenadas do ponto, em ordem x, y, z z, z, y, z.

Pode servir a você: variável nominal: conceito e exemplos

Se o ponto pertence a um avião, uma das coordenadas será 0 e, se estiver em algum dos eixos, duas das coordenadas serão 0, exceto que correspondente à localização do ponto, exceto a origem, que, como como disse antes, tem coordenadas (0,0.0).

Os seguintes exemplos esclarecem o acima.

Exemplos

Exemplo 1

Um ponto P no eixo x é expresso através de coordenadas p (x, 0, 0). Observe que a origem, destacada em vermelho na figura a seguir, tem coordenadas ou (0, 0, 0).

Quando o ponto está à direita da origem, ele tem coordenadas x positivas, enquanto se estiver à esquerda, é negativo. Por exemplo, o P1 Blue Point possui coordenadas (6,0,0), enquanto o ponto P2 em verde, possui coordenadas (-9,0,0).

Exemplo 2

Na figura seguinte, existem dois eixos, sendo o X eixo o eixo horizontal e o Eixo y O vertical. Com isso, basta representar pontos no avião, sendo duas coordenadas necessárias. A origem ou é o ponto (0,0).

Observe que a disposição dos eixos divide o plano em quatro regiões chamadas quadrantes. Os eixos acima e à direita da origem são designados com um sinal positivo, enquanto abaixo e à esquerda eles são distinguidos com um sinal negativo.

Então, os pontos cujas coordenadas são positivas, correspondem ao primeiro quadrante ou quadrante i. O ponto verde tem coordenadas (2,3) e está no quadrante i.

Por sua vez, o ponto vermelho tem coordenadas (-3,1) e está no quadrante II, enquanto as coordenadas do ponto azul são (-1.5; -2.5) e está no quadrante III.

Pode atendê -lo: fatorização comum: exemplos e exercícios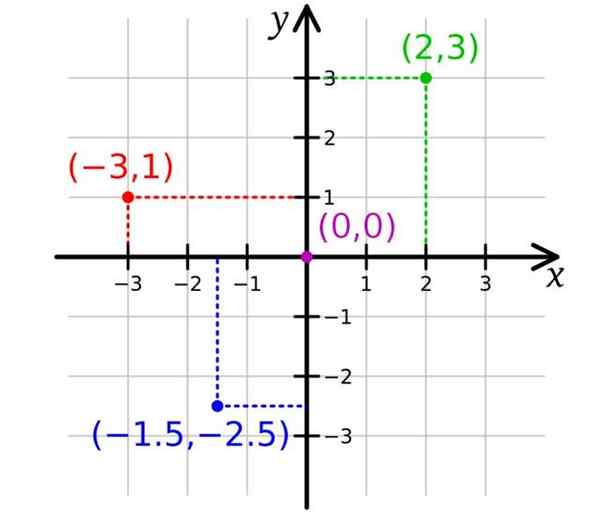 Plano cartesiano. Fonte: Wikimedia Commons

Exemplo 3

A seguir é um exemplo de um ponto no espaço. Suas coordenadas são x = 6, y = 10 e z = 8, portanto, p (6,10,8).

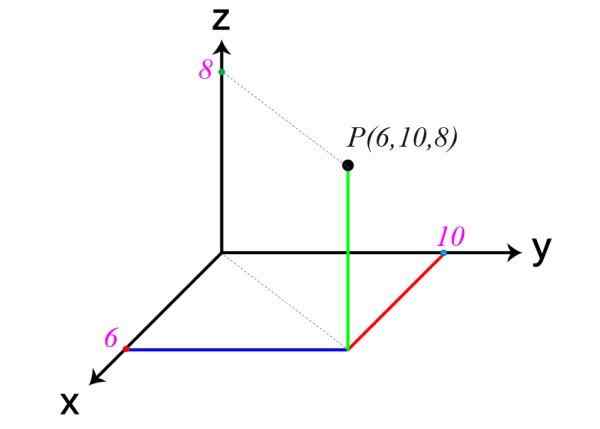Outro exemplo de eixos cartesianos

Na figura do começo, é avisado que os planos XY, XZ e ZY dividem o espaço em oito regiões, chamadas Ictaves. Ponto P do exemplo está no primeiro octante.

Referências

1. Alexander, d. (2013). Geometria. 5 ª. Edição. Cengage Learning.
2. Larson, r. (2012). Pré -cálculo. 8º. Edição. Cengage Learning.
3. Stewart, J. (2007). Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
4. O avião cartesiano. Recuperado de: DL.UNCW.Edu.
5. Weisstein, e. Coordenadas cartesianas. Recuperado de: Mathworld.Volfrâmio.com