Segundo equilíbrio, explicação, exemplos, exercícios

O Segunda condição de equilíbrio Ele estabelece que a soma dos torques ou momentos produzidos por todas as forças que agem em um corpo, independentemente de que ponto são calculadas, devem ser anuladas para que o referido corpo esteja em equilíbrio estático ou dinâmico.

Denotando o torque ou momento de força através da carta grega τ, matematicamente, é expresso da seguinte maneira:

∑ τ = 0

figura 1. Para equilibrar o balancim, é necessário aplicar a segunda condição de equilíbrio. Fonte: pxhere.

A letra ousada indica a natureza vetorial do momento, que deve ser anulada em relação a qualquer ponto que seja escolhido como um centro de spin. Dessa forma, cancelando o torque líquido, é garantido que o objeto não comece a girar ou girar.

No entanto, se o objeto já estava girando anteriormente e o torque líquido desaparece de repente, a rotação continuará, mas com rapidez angular constante.

A segunda condição de equilíbrio é usada em conjunto com a primeira condição, que diz que a soma das forças em um corpo deve ser anulada, para que não se mova, ou que, se o fizer, é com movimento retilíneo uniforme:

∑ F = 0

Ambas as condições se aplicam a corpos estendidos, aqueles cujas dimensões são mensuráveis. Quando um objeto deve ser uma partícula, não faz sentido falar sobre rotações, e a primeira condição para garantir o equilíbrio é suficiente.

Exemplos

A segunda condição de equilíbrio é revelada em inúmeras situações:

Ao subir as escadas

Ao apoiar uma escada no chão e na parede, precisamos o suficiente para esfregar, especialmente no chão, para garantir que a escada não deslize. Se tentarmos subir em uma escada apoiada em um piso oleoso, molhado ou escorregadio, não é difícil antecipar que cairemos.

Para poder usar a escada com confiança, é necessário que esteja em equilíbrio estático durante a escalada e quando está na etapa necessária.

Pode atendê -lo: Plutão (Planet Dwarf)

Movendo um armário

Quando você deseja mover um mobiliário alto como armário, ou qualquer peça cujo alto seja maior que o largo, é conveniente empurrar em um ponto baixo, para evitar a derrubada, dessa maneira é mais provável que os móveis deslizem em vez disso de girar e deitar.

Em tais circunstâncias, os móveis não estão necessariamente em equilíbrio, pois poderiam ser movidos rapidamente, mas pelo menos não viraria.

Varandas

As varandas que se destacam nos edifícios devem ser construídas, garantindo que, embora haja muitas pessoas no topo, elas não giram e colaps.

Dielétrico em campos elétricos externos

Ao colocar um material dielétrico em um campo elétrico externo, as moléculas se movem e giram para adotar uma posição de equilíbrio, criando um campo elétrico dentro do material.

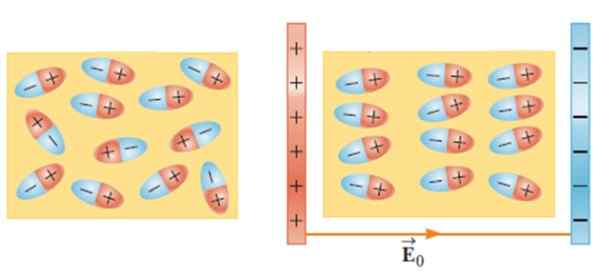Figura 2.- Sem campo elétrico externo, os dipolos são randomizados (à esquerda). O campo externo aplica um torque em moléculas dielétricas e estas são reorganizadas. Fonte: Serway, r. Física para Ciência e Engenharia.

Esse efeito torna a capacidade de um condensador aumentar quando um material como vidro, borracha, papel ou óleo é introduzido entre sua armadura.

Sinais e lâmpadas

É comum que muitas instalações pendam avisos na parede de construção, para que sejam visíveis para os transeuntes.

O pôster é preso por uma barra e um cabo, ambos fixos na parede usando suportes. As várias forças que ato devem garantir que o pôster não caia, para o qual as duas condições de equilíbrio entram em ação.

Um refletor em um parque também pode ser colocado dessa maneira, como na figura a seguir:

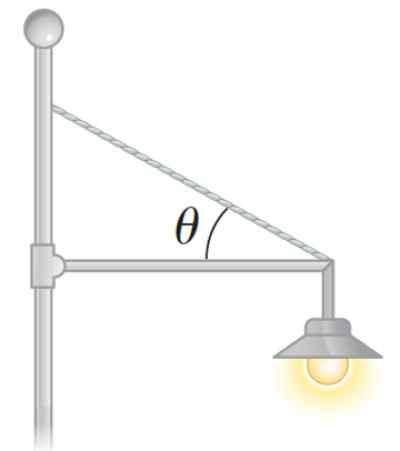Figura 3. Uma lâmpada de equilíbrio estático. Fonte: Serway. Física para Ciência e Engenharia.

Como calcular o torque líquido ou o momento líquido de uma força?

O torque ou momento de força, denotado por τ qualquer M Em alguns textos, é sempre calculado em relação a algum ponto em que o eixo de rotação passa.

É definido como o produto vetorial entre o vetor de posição r, isso é direcionado do referido eixo até o ponto de aplicação da força e força F:

Pode servir a você: Equilíbrio termodinâmico: classes e aplicações

τ = r × F

Sendo um vetor, é necessário expressar o torque dando sua magnitude, direção e significado. A magnitude é dada por:

τ = rf.sin θ

Regra correta para o produto vetorial

Quando o problema está no plano, o endereço de torque é perpendicular ao papel ou à tela e a direção é determinada pela regra da mão direita, na qual o índice aponta para r, O dedo médio F e o polegar sinaliza dentro ou fora de papel.

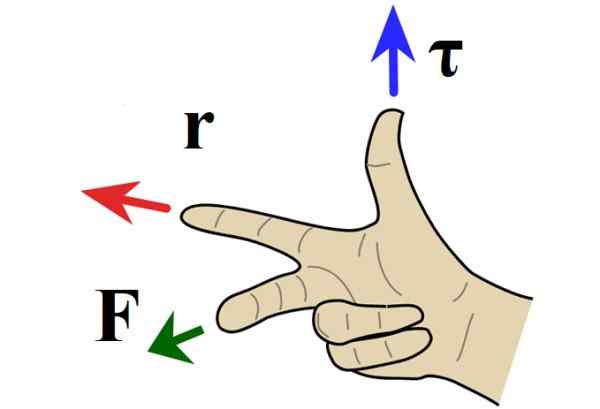Figura 4. Regra da mão direita para produto vetorial. Fonte: Wikimedia Commons.

Quando o torque aponta para fora do papel, a rotação está na direção oposta às agulhas do relógio e recebe um sinal positivo por convenção. Se o torque for direcionado na folha, a rotação está na direção das mãos e sinal negativo.

Para encontrar o torque líquido, um ponto conveniente para o cálculo é escolhido, que pode ser aquele em que a maior quantidade de forças age. Nesse caso, o momento dessas forças é nulo, para ter um vetor de posição r de magnitude 0.

Você pode escolher qualquer ponto que ofereça informações suficientes para limpar o desconhecido que pede que o problema seja resolvido. Vamos ver com mais detalhes então.

Exercício resolvido

O refletor da figura a seguir tem 20 kg de massa e é apoiado por uma barra fina horizontal, de massa desprezível e comprimento L, que é articulada para um post. O cabo, também a luz, o que ajuda a sustentar o refletor forma um ângulo θ = 30 º com a barra. Calcular:

a) A tensão no cabo

b) a magnitude da força f de que o posto exerce na barra através da dobradiça.

Solução

Aplicaremos a primeira condição de equilíbrio ∑ F = 0 para as forças mostradas no diagrama:

Pode servir você: calor absorvido: fórmulas, como calculá -lo e exercícios resolvidos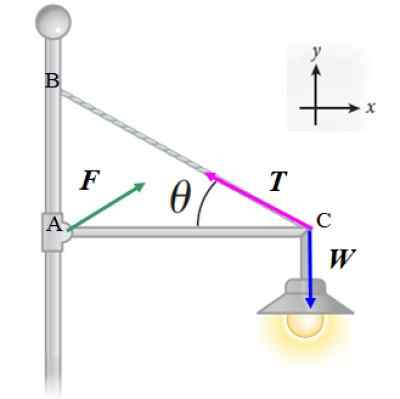

F + T + W = 0

Observe que a magnitude e a direção de F Eles ainda estão para ser determinados, mas assumimos que ele tem dois componentes: f_x e f_e. Dessa forma, temos duas equações:

F_x -T. cos θ = 0

F_e - W + t⋅ sin θ = 0

Agora vamos aplicar a segunda condição de equilíbrio, escolhendo o ponto A, pois não sabemos a magnitude de F nem o de T. Ao escolher esse ponto, o vetor r_PARA é nulo, portanto, o momento de F é nulo e a magnitude de F Não aparecerá na equação:

-W⋅l + t⋅sen θ⋅l = 0

Portanto:

T.sin θ.L = w.eu

T = w/sen θ = (20 kg x 9.8 m/s²) / Sin 30 º = 392 n

Conhecendo a magnitude de t, podemos limpar o componente f_x:

F_x = T⋅ cos θ = 392 cos 30º n = 339. 5 n

E então componente f_e:

F_e = W - t⋅ sin θ = (20 kg x 9.8 m/s²) - 392⋅sen 30 º = 0

Então podemos expressar F Então:

F = 339.5 n x

É, portanto, uma força horizontal. Isso ocorre porque consideramos que o bar tinha peso desprezível.

Se o ponto C foi escolhido para calcular o momento resultante, os vetores r_T e r_C Eles são nulos, portanto:

M = f_Y⋅L = 0

Conclui -se que f_e = 0. Desta forma:

- W + t⋅ sin θ = 0

T = w/ sin θ

Que é o mesmo resultado inicialmente obtido pela escolha do ponto A como o local onde o eixo de rotação passa.

Assuntos de interesse

Condições de equilíbrio.

Primeira condição de equilíbrio.

Referências

1. Bedford, 2000. PARA. Mecânica para engenharia: estático. Addison Wesley.
2. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 4. Sistemas de partículas. Editado por Douglas Figueroa (USB).
3. Giancoli, d.  2006. Física: Princípios com aplicações. 6º. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1.
5. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7º. Ed. Cengage Learning.