Ângulos nos tipos de circunferência, propriedades, exercícios resolvidos

Chamam-se Ângulos de circunferência para aqueles em que qualquer um de seus elementos é ou se cruzar em uma determinada circunferência. Entre eles estão os seguintes:

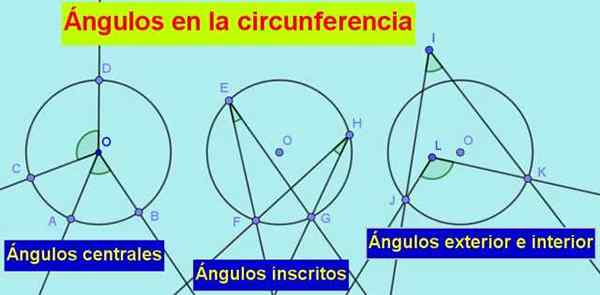
1.- Ele ângulo central, cujo vértice está no centro da circunferência e seus lados estão secando a ele, como vemos na imagem a seguir:

figura 1. Os tipos de ângulos na circunferência são: o central, o inscrito, o exterior e o interior. Fonte: f. Zapata.

2.- Ele ângulo registrado, cujo vértice está na circunferência e seus lados estão secos ou tangentes à circunferência.

3.- Ângulo externo, cujo vértice está fora da circunferência, mas seus lados estão secos ou tangentes à circunferência.

4.- Ele Ângulo interno, com o vértice dentro da circunferência e seus lados secos para o mesmo.

Todos esses ângulos mantêm certos relacionamentos entre si e isso nos leva a propriedades importantes entre os ângulos pertencentes a uma determinada circunferência.

[TOC]

Propriedades

- Ângulo central

O ângulo central é definido como aquele cujo vértice está no centro da circunferência e seus lados cortados na circunferência.

A medida de Radianes de um ângulo central é o quociente entre o arco que subtende, ou seja, o arco de circunferência entre os lados do ângulo e o raio da circunferência. 

Se a circunferência é unitária, isto é, raio 1, então a medida do ângulo central é o comprimento do arco, que corresponde ao número de radianos.

Se você deseja a medida do ângulo central em graus, a medida é multiplicada em radianos pelo fator 180º/π.

Os instrumentos de medição de ângulos, como o transportador e o goniômetro, sempre usam um ângulo central e o comprimento do arco sugerido.

Pode atendê -lo: derivados parciais: propriedades, cálculo, exercícios

Eles são calibrados em graus sexagesimal, o que significa que sempre que um ângulo é medido com eles, na parte de trás o que é medido é o comprimento do arco subtendido pelo ângulo central.

Propriedade

A medida de um ângulo central em Radianes é igual ao comprimento do arco que subtinas ou interceptações divididas pelo comprimento do raio.

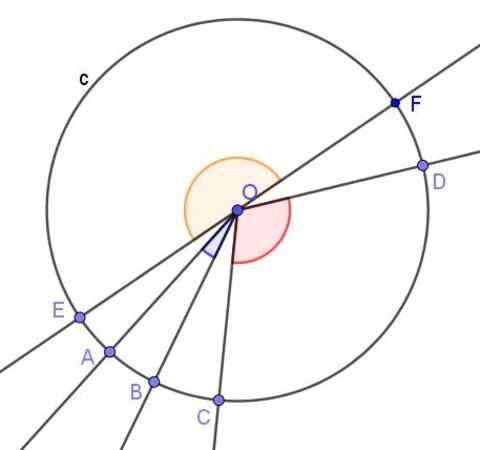Figura 2. Três ângulos centrais são mostrados. Um agudo, o outro obtuso e um apartamento. Fonte: f. Zapata.

- Ângulo registrado

O ângulo registrado de uma circunferência é aquele que tem seu vértice na circunferência e sua semi -estima é seca ou tangente à mesma. 

Suas propriedades são:

Propriedades

-O ângulo registrado é convexo ou plano.

-Quando um ângulo inscrito intercepta o mesmo arco que o ângulo central, a medida do primeiro será metade da do segundo.

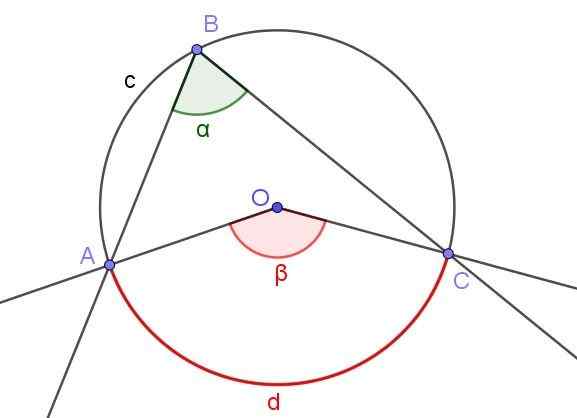Figura 3. Ângulo registrado porte e ângulo central porte que subtita o mesmo arco a⌒c. Fonte: f. Zapata.

A Figura 3 mostra dois ângulos porte e porte que intercepam o mesmo arco de circunferência A⌒C.

Se a medida do ângulo registrado for α, a medida β do ângulo central é o dobro da medida do ângulo registrado (β = 2 α) porque ambos subtraem o mesmo arco medido d D.

- Ângulo externo

É o ângulo cujo vértice está fora da circunferência e cada um de seus lados corta a circunferência em um ou mais pontos.

Propriedade

-Sua medida é igual à semi -expressa (ou diferença dividida por 2) dos ângulos centrais que interceptam os próprios arcos.

Para garantir que a medida seja positiva, o semi -Express deve ser sempre o ângulo central da maior medida, menos a medida do ângulo central inferior, como ilustrado na figura a seguir.

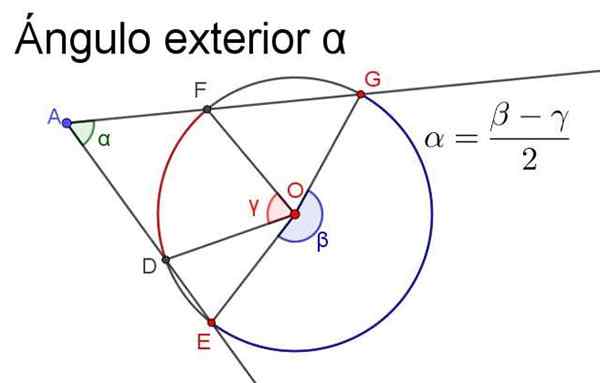Figura 4. O ângulo externo α é igual à semi -referência dos centrais que subtem os mesmos arcos. Fonte: f. Zapata.

- Ângulo interno

O ângulo interno é aquele cujo vértice está dentro da circunferência e seus lados cortados na circunferência.

Pode atendê -lo: Coeficiente de determinação: fórmulas, cálculo, interpretação, exemplos

Propriedade 

Sua medida é igual ao semi -grupo do ângulo central que subtende o mesmo arco, além do ângulo central que subtende o mesmo arco que seu ângulo de extensão (este é o ângulo interno formado pelo semi -forte complementar aos do original ângulo interno).

A figura a seguir ilustra e esclarece a propriedade do ângulo interno.

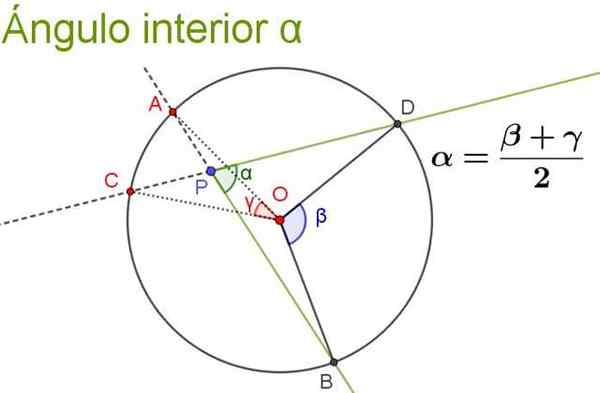Figura 5. O ângulo interno α é igual ao semi -sísmico dos ângulos centrais que subtem os mesmos arcos que ele próprio. Fonte: f. Zapata.

Exercícios resolvidos

- Exercício 1

Suponha que um ângulo inscrito no qual um de seus lados passa pelo centro da circunferência, como mostrado na Figura 6. O raio da circunferência é OA = 3 cm e o arco d tem um comprimento de π/2 cm. Determinar o valor dos ângulos α e β.

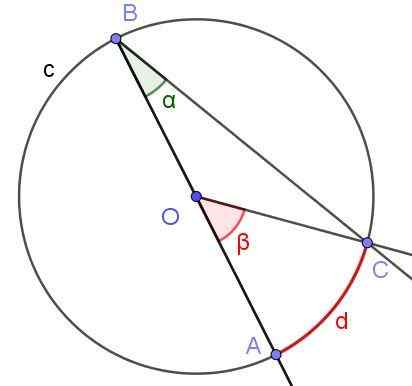Figura 6. Ângulo registrado porte com o lado [BA) através do ângulo O e Central porte.Fonte: f. Zapata.

Solução

Nesse caso, é formado o Triange de Isoceles de espuma, já que [oc] = [ob]. Em um triângulo de isósceles, os ângulos adjacentes à base são os mesmos, portanto, eles precisam portebCo = ϩABC = α. Por outro lado, ϩcob = 180º - β. Considerando a soma dos ângulos internos do triângulo Cob que você tem:

α + α + (180º - β) = 180º

De onde se segue que 2 α = β, ou o que é equivalente a = β/2, que confirma a propriedade (3) da seção anterior, que a medida do ângulo registrado é metade do ângulo central, quando ambos os ângulos subtraem A mesma corda [AC].

Agora, continuamos a determinar os valores numéricos: o ângulo β é central e sua medida em Radianes é a razão entre o arco d e o raio r = oa, então sua medida é:

β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30º.

Pode servir a você: quadrilateral: elementos, propriedades, classificação, exemplos

Por outro lado, já havia sido afirmado que α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º. 

- Exercício 2

Na Figura 7, os ângulos α₁ e β₂ tem a mesma medida. Além do ângulo β₁ Mede 60º. Determinar os ângulos β e α.

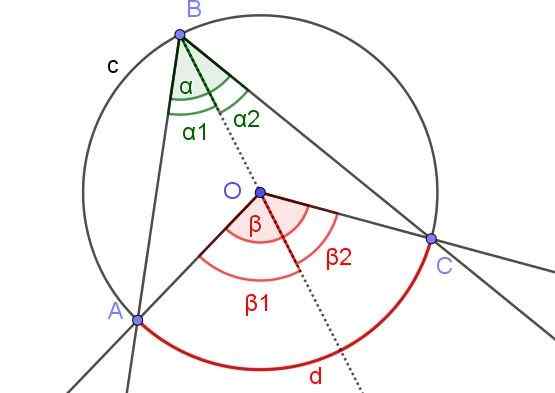Figura 7. Na Figura α₁ = β₂ e β₁ = 60º. Determinar os valores de β e α. Fonte: f. Zapata.

Solução

Nesse caso, existe um ângulo inscrito porteBC no qual o centro ou a circunferência está dentro do ângulo.

Devido à propriedade (3) você tem α₂ = β₂ /2 e α₁ = β₁ /2. Como:

α = α₁ + α₂ e β = β₁ + β₂

Você tem, portanto:

α = α₁ + α₂ = β₁ /2 + β₂ /2 = (β₁ + β₂) / 2 = β / 2.

Isto é, de acordo com as propriedades:

α = β / 2

Como nos dizem que β₁ = 60º então:

α₁ = β₁ / 2 = 60º / 2 = 30º.

Eles também nos dizem que α₁ = β₂ Então segue isso:

β₂ = 30º.

O ângulo β é:

β₁ + β₂ = 60º + 30º = 90º.

E como α = β / 2, então:

α = 90º / 2 = 45º. 

Em conclusão:

β = 90º e α = 45º.

Referências

1. Baldor, a. 1973. Geometria e trigonometria. Editorial cultural da América Central.
2. E. PARA. 2003. Elementos de geometria: com exercícios e geometria da bússola. Universidade de Medellin.
3. Geometria 1ª. Ângulos na circunferência. Recuperado de: edu.Xunta.é.
4. Toda ciência. Exercícios resolvidos de ângulos na circunferência. Recuperado de: Francesphysics.Blogspot.com
5. Wikipedia. Ângulo registrado. Recuperado de: é.Wikipedia.com