Tipos de seções cônicas, aplicações, exemplos

As Seções cônicas São as curvas que são obtidas interceptando um avião com um cone. Existem várias maneiras de fazer isso; Por exemplo, se o plano for passado perpendicularmente ao eixo axial do cone, uma circunferência é obtida.

Inclinando -se o plano um pouco em relação ao eixo axial do cone, uma elipse é obtida, uma curva que é fechada, mas se a inclinarmos ainda mais uma parábola ou uma hipérbole é obtida, como pode ser visto na animação da Figura 1.

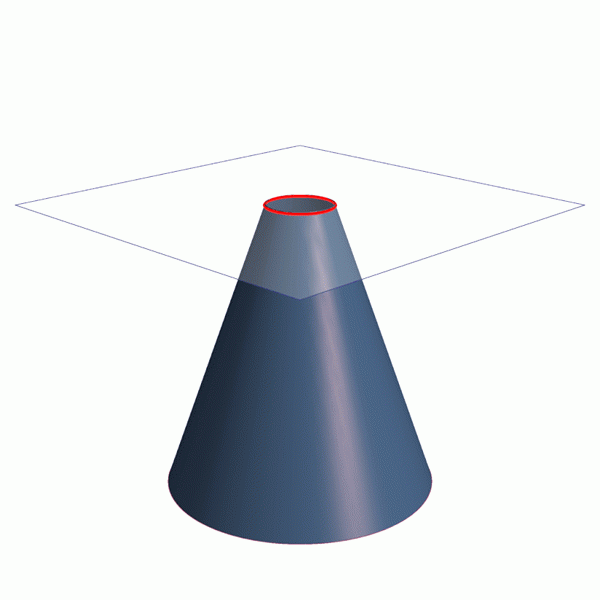Animação que mostra como obter as quatro seções cônicas: circunferência, parábola e hiperbola elipse. Fonte: Wikimedia Commons. Linhas / cc0

As seções cônicas fazem parte da natureza e do mundo ao nosso redor. Engenharia, Arquitetura e Astronomia são ramos importantes de conhecimento que fazem uso dos cônicos.

[TOC]

Condições para seções cônicas

As seções cônicas são definidas como locais geométricos que satisfazem as seguintes condições:

Parábola

É o local geométrico de todos os pontos que estão em um plano equidistante para um ponto fixo chamado foco F e uma linha reta também fixada, chamada diretivo.

Elipse

Um ponto plano pertence a uma elipse se a soma das distâncias entre esse ponto e dois outros pontos fixos, chamados Focos e localizado no Eixo principal da elipse, permanece constante.

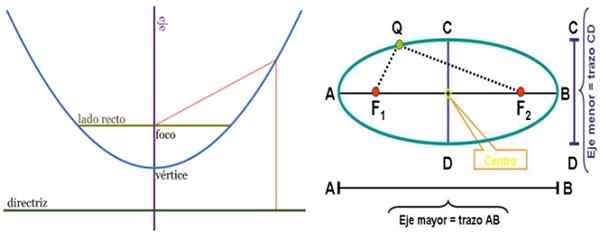A parábola à esquerda e a elipse à direita, com seus respectivos elementos. Os focos são pontos com muitas aplicações. Fonte: Wikimedia Commons.

Circunferência

É o local geométrico de todos os pontos que mantêm a mesma distância para outro ponto chamado Centro. Esta distância é o rádio da circunferência.

Pode servir a você: Distância euclidiana: conceito, fórmula, cálculo, exemplo

Hipérbole

Conjunto de pontos no avião de modo que a diferença entre sua distância e dois pontos fixos chamados Focos, é constante.

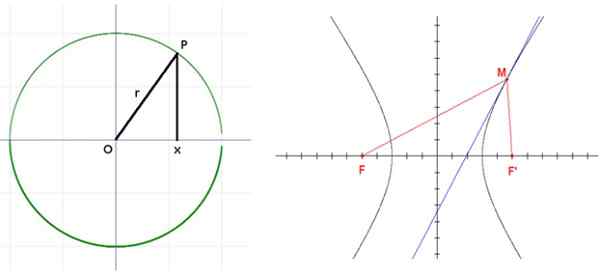Hiperbola com focos f e f. Fonte: Wikimedia Commons.

Formulários

Vejamos alguns dos aplicativos de seções cônicas:

Parábolas  

-Quando um objeto é lançado, a trajetória a seguir tem uma forma de parábola.

-As parábolas têm aplicações notáveis ​​de engenharia, por exemplo, nas pontes suspensas que os cabos se apressam na forma de parábolas.

-As parábolas também são boas para fazer refletores e telescópios. Isso é graças a uma propriedade interessante: ao colocar uma luminária no foco de uma superfície de seção transversal parabólica, a luz viajará em raios paralelos para o eixo parábola.

-Se os raios luminosos paralelos ao eixo de simetria se aproximarem da superfície parabólica, ele os concentra no foco, uma circunstância usada para fazer telescópios refletores, como o telescópio Hale de Monte Palomar.

Elipses

-Os planetas do sistema solar se movem após trajetórias elípticas, bem perto da circunferência no caso dos principais planetas, a terra incluída. O sol não está no centro, mas em um dos holofotes.

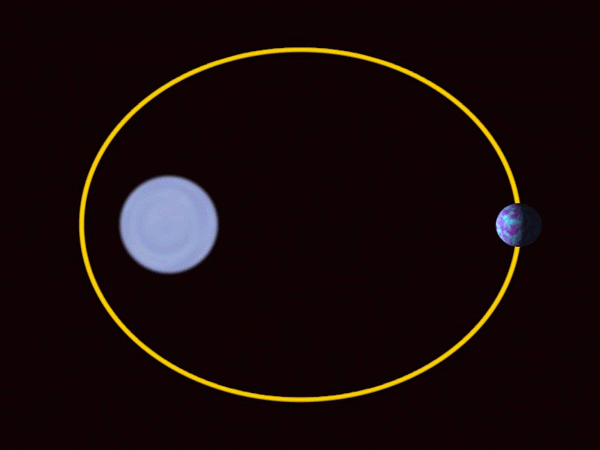Os planetas do sistema solar se movem em órbitas elípticas com o sol em um dos holofotes. Fonte: Wikimedia Commons.

-A elipse é amplamente utilizada na arquitetura como um elemento decorativo e de design.

-Ao colocar um refletor em um dos holofotes de uma elipse, a luz é refletida em direção ao outro foco. O mesmo acontece com o som. É por isso que em salões em forma de Ellipse, que falam em silêncio em um foco são claramente ouvidos por ouvintes localizados no outro foco.

Pode servir você: prisma hepagonal

-Esta mesma propriedade tem uma aplicação surpreendente no campo da medicina. Cálculos renais podem ser destruídos pelo som. As ondas de ultrassom de grande intensidade são geradas em um dos focos de uma banheira elíptica cheia de água, e o paciente está localizado no outro foco. As ondas sonoras afetam e refletem no cálculo e, com sua energia, elas a fragmentam em pequenos pedaços, que a pessoa então expulsa facilmente durante a micção.

Hiperbolas

-Alguns cometas no sistema solar seguem trajetórias hiperbólicas, sempre com o sol em um dos focos.

-Hiperbolas focos também são muito interessantes para estudar os fenômenos da reflexão das ondas. Por ejemplo, al dirigir un haz de luz al foco de un espejo parabólico esta se refleja en el otro foco, una propiedad muy útil para construir telescopios, ya que la luz puede enfocarse en un espejo parabólico y ser redirigida a otro lugar más apropiado según o desenho.

-As torres de resfriamento de usinas nucleares têm silhueta em forma de hiperbolas.

-Antes do advento dos clínicos gerais, hiperbolas eram usadas na navegação para localizar barcos. Os navios transportados a bordo emitidos simultaneamente pelas estações Radio A e B e um computador foi responsável por registrar as diferenças dos tempos de chegada dos sinais, para transformá -los em diferenças de distâncias de distâncias. Dessa maneira, o navio está localizado no ramo de uma hipérbole.

O procedimento é repetido com outras duas estações da Rádio C e D, que coloca o navio no ramo de Outra hipérbole. A posição definitiva do barco é a interseção de ambas as hiperbolas.

Pode atendê -lo: função crescente: como identificá -lo, exemplos, exercícios

Circunferências

-A chegada da roda mudou o curso da história.

-O movimento circular é muito comum, muitas peças giram para produzir vários efeitos, de moinhos a fãs.

-Embora as trajetórias dos principais planetas sejam elípticas, as trajetórias circulares são boas abordagens em muitos casos.

-As circundas são elementos frequentes em arquitetura, design, engenharia e construção. A lista de formas circulares ou de disco é interminável: moedas, CDs, relógios e muito mais.

Exemplos

Depois, há dois cônicos no avião, um círculo e uma elipse.

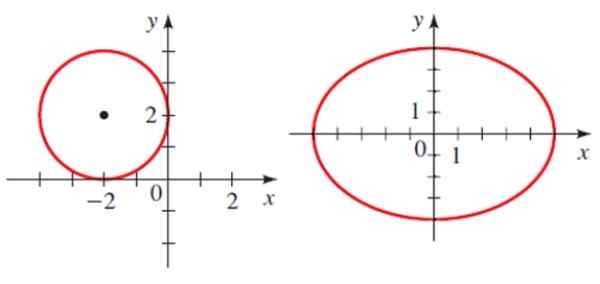Exemplos de seções cônicas: um círculo e um elipse. Fonte: Stewart, J. Pré -cálculo.

Cada um tem uma equação analítica:

Circunferência

(X-h)² + (e que)² = R²

Onde H e K são as coordenadas do centro e R é o rádio. Para a circunferência mostrada na figura, a equação é:

(x+2)² + (Y-2)² = 4

Elipse

A equação Ellipse cujo centro é o ponto de coordenada (H, k):

[(X-H)² /para² ]+ [(y-k)² /b² ] = 1

Onde A e B são os semi -pilhas da elipse. Para a elipse mostrada, o centro está no ponto 0.0, o maior semi -o mesmo é o mesmo e o semije menor é 4. Portanto, sua equação é:

(x² /25)+ (e² / 16) = 1

Referências

1. Hoffman, J. Seleção de questões de matemática. Volume 2.
2. Jiménez, r. 2008. Álgebra. Prentice Hall.
3. Stewart, J. 2006. Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
4. Wikipedia. Seção cônica. Recuperado de: é.Wikipedia.org.
5. Zill, d. 1984. Álgebra e trigonometria. McGraw Hill.