Regra da mão direita

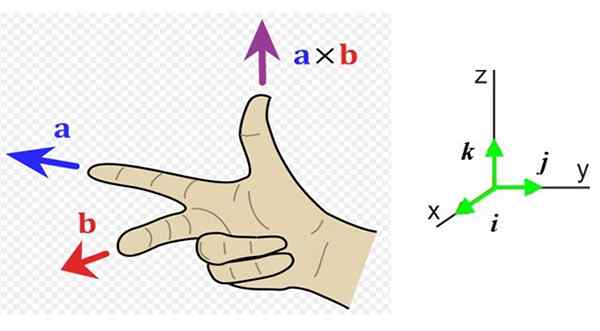figura 1. Regra da mão direita. Fonte: Wikimedia Commons. ACDX [CC BY-S (http: // criativecommons.Org/licenças/BY-SA/3.0/]].

Qual é a regra da mão direita?

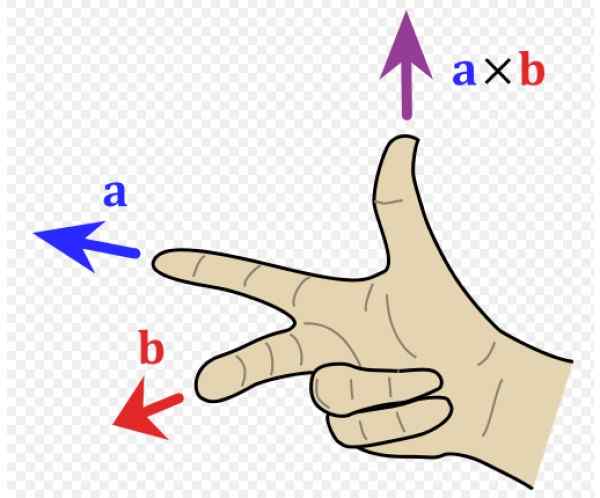
O regra da mão direita É um recurso mnemônico para estabelecer a direção e a direção do vetor resultante de um produto vetorial ou produto cruzado. É amplamente utilizado na física, pois existem magnitudes importantes do vetor que são o resultado de um produto vetorial. É o caso de torque, força magnética, momento angular e momento magnético, por exemplo.

Ser dois vetores genéricos para e b cujo produto cruzado é para x b. O módulo desse vetor é:

para x b = para.b.sin α

Onde α é o ângulo mínimo entre para e b, Enquanto A e B representam seus módulos. Para distinguir vetores de seus módulos, letras em negrito são usadas.

Agora precisamos conhecer a direção e o significado deste vetor, por isso é conveniente ter um sistema de referência com as três direções do espaço (Figura 1 direita). Os vetores da unidade Yo, J e k Eles apontam respectivamente para o leitor (fora da página), para a direita e para cima.

No exemplo da Figura 1 à esquerda, o vetor para está indo para a esquerda (endereço e dedo negativo e indicador da mão direita) e o vetor b vai para o leitor (endereço x dedo médio positivo da mão direita).

O vetor resultante para x b tem a direção do polegar, na direção z positivo.

Segunda regra da mão direita

Esta regra é muito usada quando há magnitudes cuja direção e significado estão girando, como o campo magnético B produzido por um fio fino e retilíneo que transporta uma corrente.

Nesse caso, as linhas de campo magnéticas são circunferências concêntricas com o fio, e a direção da curva é obtida com esta regra da seguinte forma: o polegar direito indica a direção da corrente e os quatro dedos restantes são curvos na direção do direção do campo. Ilustramos o conceito na Figura 2.

Pode servir a você: choques elásticos: em uma dimensão, casos especiais, exercícios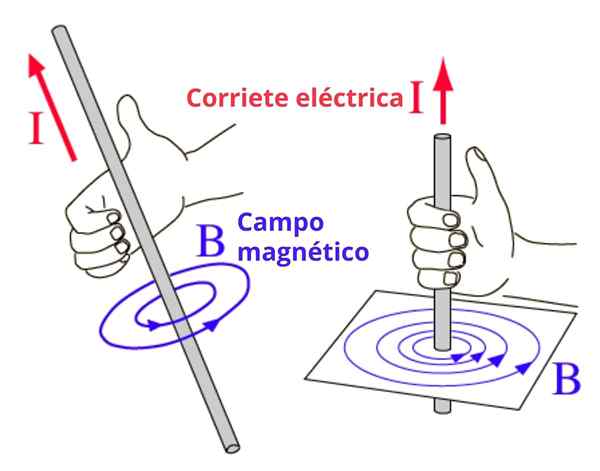Figura 2. Regra da mão direita para determinar o significado da circulação do campo magnético

Regra alternativa da mão direita

A figura a seguir mostra uma forma alternativa da regra da mão direita. Os vetores que aparecem no Iluminismo são:

• A velocidade v de uma carga pontual que.
• O campo magnético B dentro do qual a carga se move.
• F_B A força que o campo magnético exerce na carga.

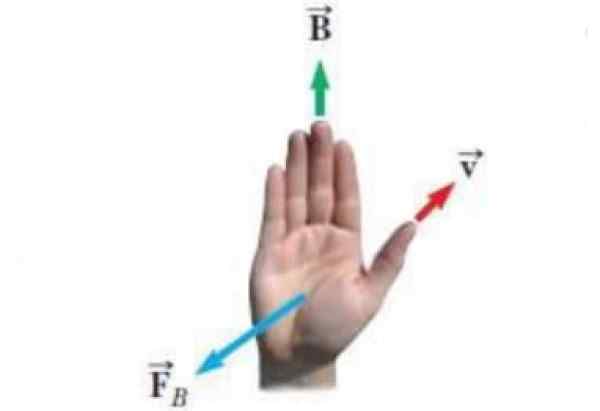Figura 3. Regra alternativa da mão direita. Fonte: Wikimedia Commons. Expertticuis [CC BY-SA (https: // CreativeCommons.Org/licenças/BY-SA/4.0)]

A equação para força magnética é F_B = qv x B e a regra da mão direita para saber a direção e o sentido de F_B Aplica -se assim: os pontos de polegar de acordo com V, os quatro dedos restantes são colocados de acordo com o campo B. Então F_B É um vetor que sai da palma da mão, perpendicular a ela, como se estivesse empurrando a carga.

Observe que F_B apontaria na direção oposta se a carga que fosse negativa, pois o produto vetorial não for comutativo. De fato:

para x B = - b x para

Formulários

A regra da mão direita pode ser aplicada a várias magnitudes físicas, vamos saber alguns deles:

Velocidade angular e aceleração

Ambas as velocidades angulares Ω Como aceleração angular α Eles são vetores. Se um objeto estiver girando em torno de um eixo fixo, é possível velocidade angular Ω.

Por sua parte, a aceleração angular α terá o mesmo endereço que Ω, Mas seu significado depende de se Ω aumenta ou diminui sua magnitude ao longo do tempo. No primeiro caso, ambos têm a mesma direção e significado, mas no segundo eles terão sentidos opostos.

Pode servir a você: Lei Watt: O que é, exemplos, aplicativos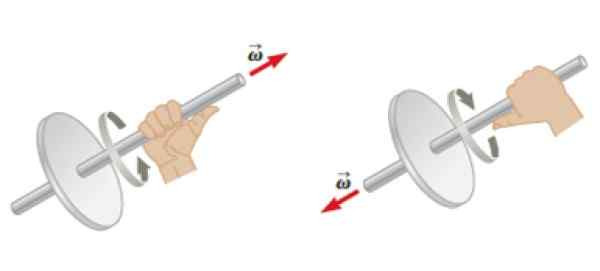Figura 4. A regra da mão direita aplicada a um objeto em rotação para determinar a direção e a direção da velocidade angular. Fonte: Serway, r. Físico.

O momento angular

O vetor angular eu_QUALQUER de uma partícula que gira em torno de um determinado eixo ou é definido como o produto vetorial de seu vetor de posição instantânea r  e a quantidade de movimento linear p:

eu = r x p

A regra direita -mão é aplicada dessa maneira: o dedo indicador é colocado na mesma direção e direção de r, O dedo médio no p, ambos em um plano horizontal, como na figura. Automaticamente o polegar se estende verticalmente para cima apontando para a direção e a direção do momento angular eu_QUALQUER.

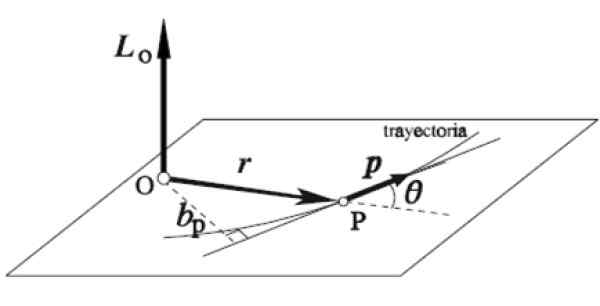Figura 5. O vetor angular. Fonte: Wikimedia Commons.

Exercícios

Exercício 1

O giro da Figura 6 está indo rapidamente com a velocidade angular Ω e seu eixo de simetria quebrado mais lentamente em torno do eixo vertical z. Este movimento é chamado precessão. Descreva as forças que agem sobre a rotação e o efeito que eles produzem.

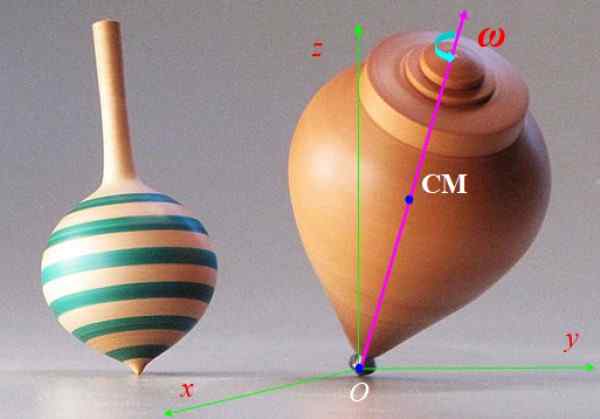Figura 6. Giro giratório. Fonte: Wikimedia Commons.

Solução

As forças que agem sobre a rotação são normais N, aplicado ao ponto de suporte com o solo ou mais o peso mg, aplicado no centro de massa CM, com g O vetor de aceleração da gravidade, direcionado verticalmente para baixo (veja a Figura 7).

Ambas as forças são equilibradas, portanto o spin não se move. No entanto, o peso produz um torque ou torque τ Rede sobre o ponto ou, dado por:

τ_QUALQUER = r_QUALQUER x F, com F = Mg.

Como r e mg Eles estão sempre no avião enquanto a rotação gira, de acordo com a regra da mão direita o torque τ_QUALQUER Está sempre localizado no avião XY, perpendicular ambos a r como g.

Observe que N não produz um torque em relação a O, porque seu vetor r Sobre ou é nulo. Esse torque produz uma mudança no momento angular que causa a precessão da rotação ao redor do eixo z.

Pode servir a você: Equilíbrio termodinâmico: classes e aplicações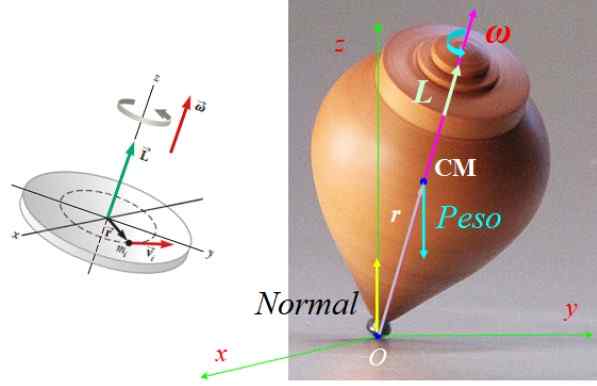Figura 7. Forças que atuam no spin e seu vetor de momento angular. Fonte da figura esquerda: Serway, r. Física para Ciência e Engenharia.

Exercício 2

Aponte a direção e a direção do vetor de momento angular eu do Trumpe da Figura 6.

Solução

Qualquer ponto do spin tem massa m_Yo, velocidade v_Yo e vetor de posição r_Yo, Quando gira em torno do eixo z. O momento angular eu_Yo da referida partícula é:

eu_Yo = r_Yo x p_Yo = r_Yo x m_Yov_Yo

Dado que r_Yo e v_Yo Eles são perpendiculares, a magnitude de eu é:

eu_Yo = m_Yor_Yov_Yo

A velocidade linear v está relacionado à velocidade angular Ω através:

v_Yo = r_YoΩ

Portanto:

eu_Yo = m_Yor_Yo (r_YoΩ) = m_Yor_Yo²Ω

O momento angular total do trompo L é a soma do momento angular de cada partícula:

L = (∑M_Yor_Yo² ) Ω

∑ m_Yor_Yo²  É o momento da inércia I da rotação, então:

eu= IΩ

Portanto eu e Ω Eles têm a mesma direção e significado, como mostrado na Figura 7.