Segunda linhas

A madeira da porta deste jardim está disposta de tal maneira que eles determinam linhas secas. Fonte: f. Zapata. Pxhere.com

Quais são as linhas secas?

No avião, o Segunda linhas Eles são aqueles que cruzam outras linhas e curvas. No caso de duas linhas, seu cruzamento é um ponto, enquanto a linha secante em uma curva, corta isso em dois ou mais pontos.

Observe cuidadosamente a cerca da figura superior. Nele foram desenhados várias cores retas, denotadas como l₁, eu₂ e eu₃. As setas de ambos os lados significam que as linhas são prolongadas indefinidamente.

Bem, as linhas l₁, eu₂ e eu₃ Eles estão secando um ao outro, já que cada par deles é cortado em pontos roxos.

Além disso, as linhas L₁ e eu₂, Como l₁ e eu₃, Eles determinam 4 ângulos um com o outro, dois deles agudos e o outro obtuso, enquanto as linhas l₂ e eu₃ Eles são perpendiculares, o que significa que os 4 ângulos determinados por eles são retos.

Duas linhas paralelas nunca podem estar secas, pois, devido à sua condição, elas não têm pontos de coincidência. Por sua vez, as linhas coincidentes não estão secas, pois têm mais de um ponto em comum.

Características das linhas de secagem

• Duas linhas secantes têm um ponto único como interseção.
• As inclinações de duas linhas de secagem devem ser diferentes. sim m₁ É a inclinação da linha l₁, e m₂ É a inclinação da linha l₂, então é cumprido que M₁ ≠ m₂.
• As inclinações de duas linhas de secagem perpendiculares entre si, cujas respectivas encostas são m₁ e m₂, Eles cumprem o relacionamento m₁ = -1/ m₂. Além disso, o produto escalar entre dois vetores v e ou contido nessas linhas é nulo, uma vez que a definição de produto escalar é v ou = v ∙ u ∙ cos θ, sendo θ o ângulo entre os vetores.
• Uma linha pode ser secante a uma curva ou outra figura geométrica.
• Ao se cruzar, duas linhas de secagem geram 4 ângulos, idênticos dois a dois ou idênticos um ao outro.

Pode atendê -lo: equações fracionárias

Como saber se duas linhas estão secas

A partir das características das linhas de secagem descritas acima, é possível estabelecer três critérios para saber se duas linhas estão secas:

-Comparando as encostas. Se estes forem diferentes, as linhas estão secas.

-Realizando o produto escalar entre dois vetores que estão contidos nessas linhas, chamados Diretores. Se o produto escalar for vazio, as linhas estão secas e perpendiculares e, se não for zero, é possível conhecer o ângulo mínimo entre eles, que é o ângulo agudo existente entre as linhas.

Desde que este ângulo seja diferente de 0º, as linhas estão secas e se for igual a 0º, então são linhas paralelas.

-Calcular diretamente o ângulo agudo que existe entre as linhas, conhecido suas encostas. Isso pode ser feito através da fórmula que relaciona a tangente do referido ângulo com as encostas.

Deixe m₁ e m₂ as encostas e θ o ângulo agudo entre elas. A tangente de θ é dada por:

Tipos de linhas de secagem

Quando duas linhas estão secando, elas podem ser os seguintes tipos:

• Oblíquo, Se quando cortados, eles formam dois ângulos agudos e dois ângulos obtusos. Esses ângulos são suplementares, ou seja, a soma da medida do ângulo mais a do ângulo obtusa é igual a 180º. No total, a soma dos 4 ângulos é igual a 360º.
• Perpendicular, Aqueles que estão se cruzando 4 ângulos iguais a 90º.

Como encontrar a interseção entre duas linhas

Se duas linhas estão secando, elas têm apenas um ponto de corte, que está resolvendo o sistema de duas equações lineares com duas incógnitas. Se as linhas forem dadas em geral: ax + por = c, o referido sistema de equações é:

Pode servir a você: Conjunto Infinito: Propriedades, Exemplos

para₁x + b₁ y = c₁

para₂x + b₂ y = c₂

Como encontrar a interseção entre uma linha e uma curva

Conhecendo as equações da linha e da curva, o sistema de equações é proposto e, cujas soluções correspondem aos pontos de interseção. Se o sistema não possui uma solução, a linha não será secante para a curva, nem se houver um único ponto de corte, pois, nesse caso, a linha é tangente à curva.

Para que a linha esteja secando, conforme declarado no início, o sistema de equações deve ter duas ou mais soluções.

Exemplos de linhas de secagem

O avião cartesiano

O avião cartesiano é determinado por duas linhas, chamadas X eixo e Eixo y, horizontal e vertical, respectivamente. Essas linhas são perpendiculares e seu ponto de interseção é chamado Origem do sistema de coordenadas, ou simplesmente origem.

A diagonal de um polígono

Um polígono é uma figura plana de três ou mais lados, que se juntam em pontos chamados vértices. Um segmento que se junta a dois vértices não consecutivos é uma diagonal do polígono, e a linha que contém o segmento é secante ao polígono em questão.

Uma corda de circunferência

A corda de uma circunferência é o segmento que se junta a dois de seus pontos. A corda principal é o diâmetro, que necessariamente passa pelo centro da circunferência. Bem, a linha que contém qualquer corda, incluindo o diâmetro, é uma linha de secagem para a circunferência.

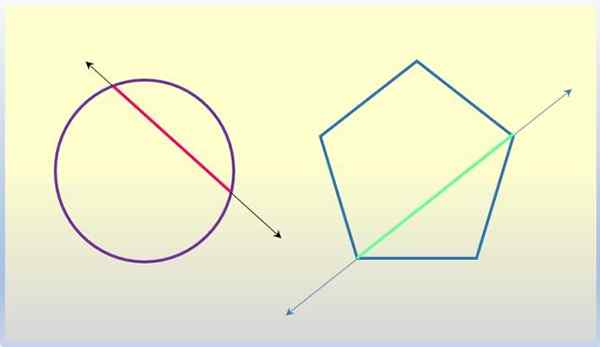Segundas linhas para figuras geométricas. Fonte: f. Zapata.

A chave cruzada

Com esta ferramenta, as nozes que seguram os pneus nas rodas dos veículos são soltas. As linhas de formulários que são secas e ao mesmo tempo perpendiculares.

Pode atendê -lo: variação proporcional

Letras de Alphabet

Algumas letras do alfabeto consistem em traços retos que determinam. Por exemplo, a letra X consiste em dois golpes que são cortados em um ponto e a letra t consiste em duas linhas perpendiculares.

Exercícios resolvidos

Exercício 1

Determine se as linhas fornecidas por:

eu₁ : y = 5x - 3

eu₂ : y = -2x+1

Solução

A inclinação de uma linha dada na forma y = mx + b é o valor de m, ou seja, o coeficiente que acompanha o x. Desde m₁ = 5 e m₂ = -2, que são diferentes, conclui -se que as linhas estão secas.

Exercício 2

Qual é o ângulo agudo entre as linhas do Exercício 1?

Solução

Os valores M são substituídos diretamente₁ = 5 e m₂ = -2 Na fórmula dada nas seções anteriores:

Portanto, o ângulo entre as linhas é θ = arctg 0.777… = 37.9º.

Exercício 3

Qual é a interseção entre as linhas dos exercícios anteriores?

Solução

O sistema de equações é proposto da seguinte maneira:

Cuja solução é: x = 4/7; y = -1/7 (pode ser resolvido por qualquer um dos métodos de resolução para sistemas de equações ou com uma calculadora).

Portanto, o ponto de interseção das linhas é: P (4/7; -1/7).

Referências

1. Geometria analítica.Informações. Segunda linhas. Recuperado de: geometriaanitics.Informações.
2. Larson, r. 2006. Cálculo com geometria analítica. 8º. Edição. McGraw Hill.
3. Linhas que cruzam. Recuperado de: ProfessorTuna.com.
4. Requena, b. Segunda linhas. Recuperado de: universoformulas.com.
5. Villena, m. Geometria analítica em R3. Recuperado de: dspace.Espol.Edu.EC.