Características, equações e exemplos de direitos obrigatórios

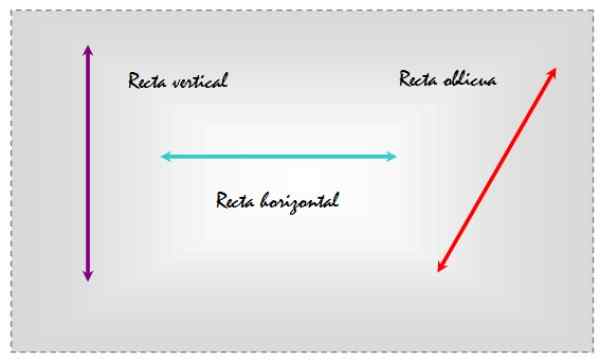
As linhas oblíquas Eles são aqueles que são inclinados, seja em relação a uma superfície plana ou outra linha que indica um endereço específico. Como exemplo, considere as três linhas desenhadas em um avião que aparece na figura a seguir.

Conhecemos suas respectivas posições relativas porque as comparamos com uma linha de referência, que geralmente é o X eixo que denota a horizontal.

figura 1. Linhas verticais, horizontais e oblíquas no mesmo plano. Fonte: f. Zapata.

Dessa maneira, escolhendo a referência horizontal, a linha esquerda é vertical, o centro é horizontal e o da direita é oblíqua, pois é inclinada em relação às linhas de referência diária.

Agora, as linhas que estão no mesmo plano, como a superfície do papel ou a tela, ocupam posições diferentes em relação uma à outra, dependendo se elas se cruzam ou não. No primeiro caso, eles estão retos secos, enquanto no segundo, são paralelos.

Por outro lado, as linhas de secagem também podem ser oblíquas ou linhas retas perpendiculares. Nos dois casos, as inclinações das linhas são diferentes, mas as linhas oblíquas se formam entre si α e β, além de 90º, enquanto os ângulos determinados pelas linhas perpendiculares são sempre 90º.

Na figura a seguir, essas definições estão resumidas:

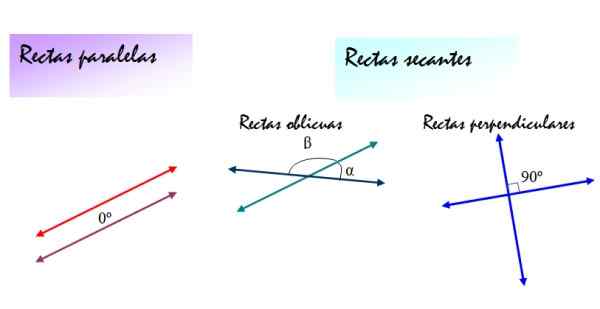Figura 2. As posições relativas entre as linhas: paralelas, oblíquas e perpendiculares diferem no ângulo que se formam. Fonte: f. Zapata.

[TOC]

Equações

Para conhecer as posições relativas das linhas no plano, é necessário conhecer o ângulo que eles se formam. Observe que as linhas são:

Pode atendê -lo: cálculo de abordagens usando diferenciais

Paralelo: Se eles têm a mesma inclinação (direção igual) e nunca se cruzam, seus pontos são equidistantes.

Coincidentes: Quando todos os seus pontos coincidem e, portanto, têm a mesma inclinação, mas a distância entre seus pontos é zero.

Secantes: Se seus brincos são diferentes, a distância entre os pontos varia e a interseção é um único ponto.

Portanto, uma maneira de saber se duas linhas no avião estão secas ou paralelas é através de sua ladeira. Os critérios de paralelismo e perpendicularidade das linhas são os seguintes:

Ser duas linhas L₁ e eu₂ pertencente a um avião, cujo pendente é respectivamente M₁ e m₂. Essas linhas são paralelas se m₁ = m₂ e eles são perpendiculares quando M₁= -1/m₂

Ao conhecer as encostas de duas linhas no avião, nenhum dos critérios acima é atendido, concluímos que as linhas são oblíquas. Conhecendo dois pontos de uma linha, a inclinação é calculada imediatamente, como veremos na próxima seção.

Você pode descobrir se duas linhas estão secas ou paralelas encontrando sua interseção, resolvendo o sistema de equações que se formam: se houver uma solução, elas estão secas, se não houver, elas são paralelas, mas se as soluções forem infinitas, as linhas são Coincidente.

No entanto, esse critério não nos informa sobre o ângulo entre essas linhas, mesmo que elas tenham interseção.

Para conhecer o ângulo entre as linhas, são necessários dois vetores ou e v que pertencem a cada um deles. Assim, é possível conhecer o ângulo que eles formam através do produto escalar dos vetores, definidos dessa maneira:

ou•v =ou.v.cos α

Equação de linha no avião

Uma linha no avião cartesiano pode ser representada de várias maneiras, como:

Pode servir a você: Equação Geral de Parábola (Exemplos e Exercícios)

-Formulário de Internet pendente: Sim m É a inclinação da linha e b É a interseção da linha com o eixo vertical, a equação da linha é y = mx +b.

-Equação geral para uma linha reta: AX + por + C = 0, onde M = a/b É a ladeira.

No plano cartesiano, linhas verticais e horizontais são casos particulares da equação da linha.

-Linhas verticais: x = a

-Linhas horizontais: y = k

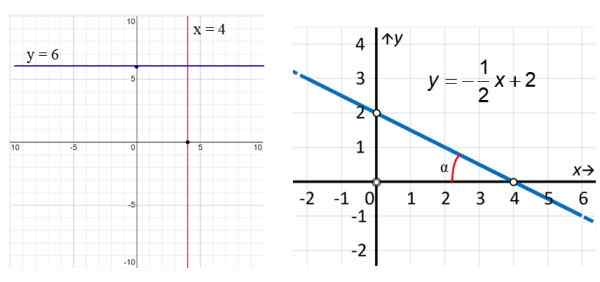Figura 3. À esquerda, a linha vertical x = 4 e a linha horizontal y = 6. À direita, um exemplo de linha oblíqua. Fonte: f. Zapata.

Nos exemplos da Figura 3, a linha vermelha vertical possui a equação x = 4, enquanto a linha paralela ao eixo x (azul) possui a equação y = 6. Quanto à linha certa, vemos que é oblíqua e, para encontrar sua equação, usamos os pontos destacados na figura: (0.2) e (4.0) desta maneira:

M = (e₂ - e₁) / (X₂ - x₁) = (2 - 0) / (0 - 4) = - ½

O corte desta linha com o eixo vertical é y = 2, Como observado nos gráficos. Com esta informação:

y = (-½) x+2

Determinar o ângulo de inclinação em relação ao eixo x é simples. Eu sinto isso:

α = arctg (2/4) = 26.6º

Portanto, o ângulo positivo do eixo x até a linha é: 180º - 26.6º = 153.4º

Exemplos de linhas oblíquas

Figura 4. Exemplos de linhas oblíquas. Fonte: Ian Patterson Wrathful [CC por (https: // criativeCommons.Org/licenças/por/2.0)]. Torre inclinada de Pisa. Pixabay.

Linhas oblíquas aparecem em muitos lugares, é uma questão de prestar atenção a encontrá -las em arquitetura, esporte, fiação de fornecimento de eletricidade, tubos e em muitos outros lugares. Na natureza, linhas oblíquas também estão presentes, como veremos abaixo:

Pode atendê -lo: regras de derivação (com exemplos)

Os raios da luz

A luz solar se espalha em uma linha reta, mas a forma arredondada da terra afeta a maneira como a luz solar afeta a superfície.

Na imagem abaixo, podemos apreciar claramente que os raios solares afetam perpendicularmente nas regiões tropicais, mas, em vez disso, chegam obliquamente à superfície nas regiões temperadas e nos pólos.

Portanto, os raios do sol viajam uma distância mais longa pela atmosfera e também o calor se espalha em uma superfície maior (veja a figura). O resultado é que as áreas próximas aos postes estão mais frias.

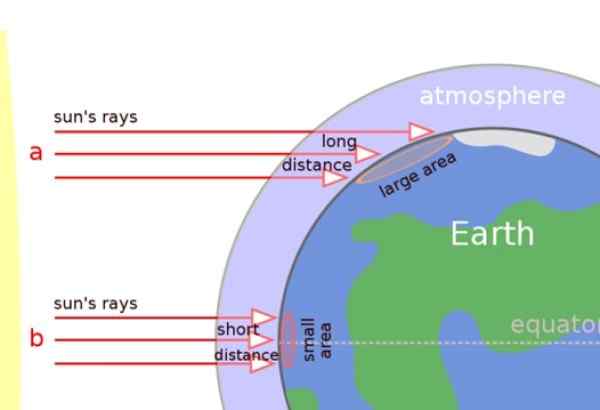Figura 5. Os raios do sol afetam obliquamente as zonas temperadas e os pólos, no entanto, são mais ou menos perpendiculares nos trópicos. Fonte: Wikimedia Commons.

Linhas que não estão no mesmo avião

Quando duas linhas não estão no mesmo avião, elas ainda podem ser oblíquas ou elogiado, Como eles também são conhecidos. Nesse caso, seus diretores não são paralelos, mas não pertencem ao mesmo plano, essas linhas não têm interseção.

Por exemplo, linhas na figura certa estão claramente em diferentes aviões. Se eles olharem de cima, observa -se que eles efetivamente cruzam, mas não têm um ponto comum. À direita, vemos as rodas de bicicleta, cujos raios parecem atravessar quando eles olham para a frente.

Figura 6. Linhas oblíquas pertencentes a diferentes aviões. Fonte: esquerda f. Zapata, Pixabay direita.

Referências

1. Geometria. Diretor vetorial de uma linha. Recuperado de: Juanbrague.é.
2. Larson, r. 2006. Cálculo com geometria analítica. 8º. Edição. McGraw Hill.
3. Matemática é um jogo. Linhas e ângulos. Recuperado de: juntadeandalucia.é.
4. Linhas que cruzam. Recuperado de: ProfessorTuna.com.
5. Villena, m. Geometria analítica em R3. Recuperado de: dspace.Espol.Edu.EC.