Área de um Pentágono regular e irregular como é tirada, exercícios

Para calcular o área de um Pentágono Primeiro, precisamos determinar se isso é regular ou não é. Um Pentágono é um polígono, uma figura plana fechada de cinco lados. Quando um polígono é regular, significa que o comprimento de seus lados é o mesmo e seus ângulos internos também.

Nesse caso, há uma fórmula para calcular a área exata do polígono comum, conhecendo algumas de suas principais características, que deduziremos mais tarde.

Dois pentágonos

Se o polígono não for regular, ou seja, tem lados de tamanhos diferentes e ângulos internos desiguais, não há uma única fórmula.

No entanto, os matemáticos encontraram estratégias de cálculo, como dividir a figura em outros com o menor número de lados, como triângulos, quadrados e retângulos, cujas dimensões são conhecidas ou facilmente calculadas.

Outro procedimento para calcular áreas de polígonos em geral, conhecendo as coordenadas de seus vértices, é o método chamado Determinantes de Gauss, que vamos descrever mais tarde.

[TOC]

Como calcular a área de um pentágono comum?

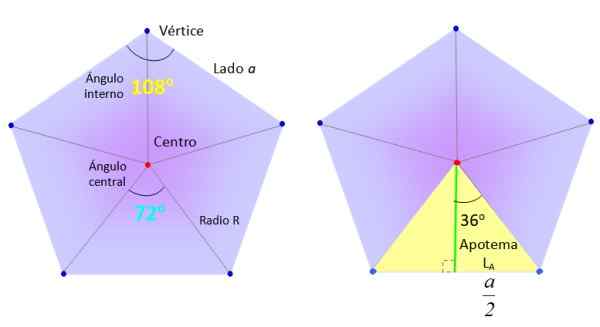
Vamos pegar um Pentágono regular do lado A, e o dividiremos em 5 triângulos iguais, como mostrado na figura, desenhando segmentos do centro (vermelho) para os vértices (azul).

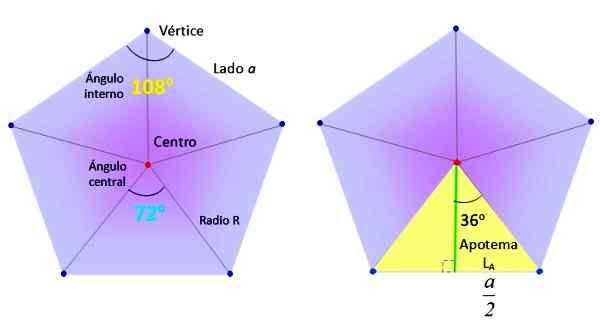Os elementos necessários para encontrar a área regular do Pentágono. Fonte: f. Zapata.

Por sua vez, os triângulos, como o Yellow em destaque à direita na figura superior, são divididos em dois retângulos iguais, graças ao segmento verde, chamado apótema.

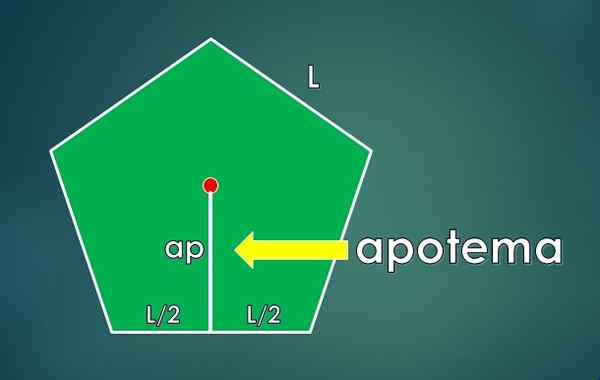
O apoteme é definido como o segmento perpendicular que se conecta ao centro do polígono com o centro de um lado. Seu comprimento é L_PARA.

A área de um triângulo retângulo de base A/2 e altura l_PARA é:

[(A/2) x L_PARA]

O Pentágono tem 10 triângulos como este; portanto, sua área é:

Pode atendê -lo: funções vetoriais

A = 10 (a/2) x L_PARA

Mas o perímetro P do Pentágono é precisamente p =10a, Portanto, a área é dada pelo semi -produto do perímetro e pela duração do apotem:

A = p x l_PARA /2

Área regular do Pentágono, conhecendo o lado a

Expressando o comprimento do apothem l_PARA Dependendo do lado A, sabendo que o ângulo indicado é metade do ângulo central, ou seja, 36º, equivalente a:

36º = π/5

Pela trigonometria elementar, por tangente do ângulo agudo 36º:

Tan (π/5) = (a/2) ÷ l_PARA

Por isso:

eu_PARA=  (A/2) ÷ tan (π/5)

Substituindo na área deduzida na seção anterior e sabendo que p = 5a:

A = p x l_PARA /2

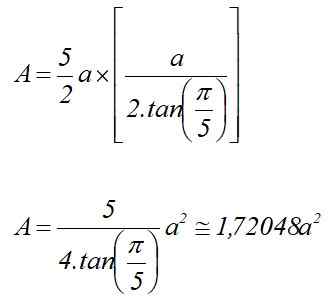
Área regular do Pentágono, conhecendo seu rádio

Ele rádio de um polígono comum é o segmento que vai do centro para um de seus vértices. Coincide com o raio da circunferência circunscrita, como mostrado na figura a seguir:

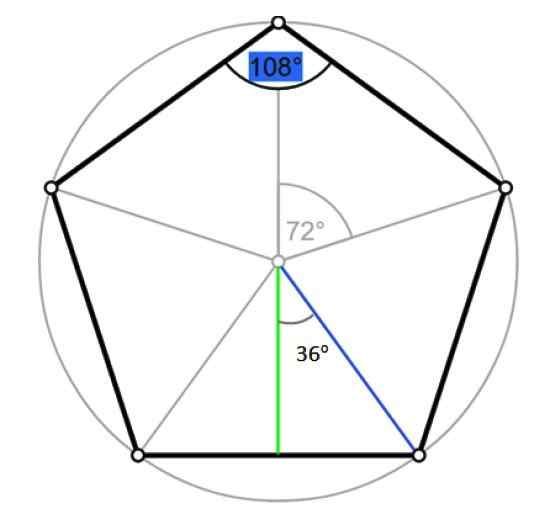Ângulos e apotem do Pentágono. Fonte: Wikimedia Commons/F. Zapata.

Seja r a medida do referido rádio, que coincide com a hipotenusa do triângulo certo delineado na figura anterior, em azul. Por trigonometria:

cos 36º = cos (π/5) = L_PARA ÷ r

E

sin 36º = sin (π/5) = (a/2) ÷ r r

Portanto:

A = p x l_PARA /2 = 5r. sin (π/5) x r. cos (π/5) = 5r² [sin (π/5) x cos (π/5)]]

Usando a fórmula de ângulo duplo:

sin (2θ) = 2 sen θ . cos θ

Temos que:

[sin (π/5) x cos (π/5)] = (1/2) sin 72º

E assim, por substituição desse valor, obtemos a seguinte fórmula para a área regular do Pentágono:

A = (5/2) r².Sen 72º

Como calcular a área de um pentágono irregular?

Como já dissemos antes, para um polígono irregular, não há uma fórmula única, mas há dois métodos que geralmente funcionam muito bem, o primeiro é chamado de triangulação e o segundo é o método dos determinantes de Gauss.

Pode atendê -lo: Teorema da existência e exclusividade: demonstração, exemplos e exercícios

Triangulação

Consiste em dividir a figura em triângulos, cuja área é mais fácil de calcular, ou também pode ser testada com outras figuras cuja área é conhecida, como quadrados, retângulos e trapezides.

Determinantes de Gauss

Outra maneira de encontrar a área irregular do Pentágono ou outro polígono irregular está colocando a figura em um sistema de coordenadas cartesianas, a fim de encontrar as coordenadas dos vértices.

Conhecidos essas coordenadas, o método dos determinantes de Gauss é aplicado para calcular a área, que é dada pela seguinte fórmula:

Onde a é a área do polígono e (x_n , e_n ) são as coordenadas dos vértices. Um polígono de N lados tem 5 vértices, para o Pentágono seria n = 5:

As barras que acompanham a fórmula são barras de módulo ou valor absoluto.

Isso significa que, embora o resultado da operação seja negativo, devemos expressá -lo com um sinal positivo e, se já for positivo, deve ser deixado com esse sinal. Isso ocorre porque uma área é sempre uma quantidade positiva.

O procedimento é chamado de determinantes de Gauss por seu criador, o matemático alemão Carl F. Gauss (1777-1855). As operações indicadas são equivalentes ao determinante de uma matriz 2 × 2, por exemplo, o primeiro determinante é:

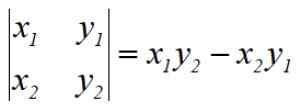
Para encontrar a área do Pentágono, devemos resolver 5 determinantes, adicione o resultado algebricamente, dividir -o por 2 e finalmente expressar a área sempre com um sinal positivo.

Exercícios resolvidos

Exercício 1

Encontre a área regular do Pentágono cujo apotem vale 4 cm e cujo lado mede 5.9 cm.

Solução

Como é um Pentágono regular e temos a medida do lado e do apotem, usamos a fórmula deduzida anteriormente:

Pode atendê -lo: Triângulo Scaleno

A = p x l_PARA /2

O perímetro p é igual a 5a = 5 x 5.9 cm = 29.5 cm.

A = 29.5 cm x 4 cm / 2 = 59 cm²

Exercício 2

Encontre a área irregular do Pentágono mostrada. As seguintes dimensões são conhecidas:

Dc ≈ de

AE = AB = 5

BC = 12

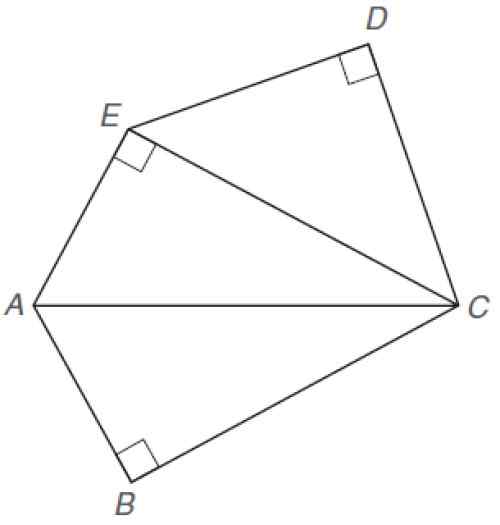Pentágono irregular. Fonte: Alexander, D. 2013. Geometria. 5 ª. Edição. Cengage Learning.

Solução

A área do Pentágono é a soma das áreas dos triângulos, que são retângulos. A declaração diz que DC ≈, portanto, ao aplicar o teorema de Pitágoras ao Triângulo da EDC, ele tem:

EC² = 2 ed². Então ec = √2.Ed.

Os triângulos AEC e ABC têm uma hipotenusa comum, que é o segmento CA, portanto:

Ea² + EC² = Ab² + Bc²

Como EA e AB medem o mesmo, é obtido que:

EC = BC = √2.Ed

Desde BC = 12, então ed = 12 / √2 = 8.485.

Com esses valores, calcularemos a área de cada triângulo e os adicionaremos no final.

Área do triângulo EDC 

Ed x dc /2 = 8.485² / 2 = 36

Área do triângulo AEC 

Ea x ec / 2 = ea x √2.Ed / 2 = 5 x √2. 8.485/2 = 30

Área do triângulo ABC 

AB X BC / 2

Então a área procurada é:

5 x 12/2 = 30

É o mesmo que o do triângulo AEC, pois ambos têm as mesmas medidas.

Área irregular do Pentágono

Finalmente, a área solicitada é a soma das áreas dos três triângulos:

A = 36 + 30 + 30 unidades = 96 unidades.

Referências

1. Alexander, d. 2013. Geometria. 5 ª. Edição. Cengage Learning.
2. Math Open Reference. Área de Polígono. Recuperado de: MathpenRef.com.
3. Fórmulas do Universo. Área de um pentágono irregular. Recuperado de: universoformulas.com.
4. Fórmulas do Universo. Área de um pentágono comum. Recuperado de: universoformulas.com.
5. Wikipedia. Pentágono. Recuperado de: é.Wikipedia.com.