Raiz quadrada de 3 (solução fácil e explicação)

A raiz quadrada de 3 é 1.73205080756887.

Pode ser expresso:

√3 = 1.73205080756887

Para saber o que é o Raiz quadrada de 3, É importante conhecer a definição da raiz quadrada de um número. Dado um número positivo "A", a raiz quadrada de "A", indicada por √a, é um número positivo "B" de modo que quando "B" é multiplicado por ele, o resultado é "A".

A definição matemática diz: √a = b sim, e somente se, b² = b*b = a. Portanto, para saber o que é a raiz quadrada de 3, ou seja, o valor de √3, um número "B" deve ser encontrado que b² = b*b = √3.

Além disso, √3 é um número irracional, que consiste em uma quantidade infinita não periódica de decimais. Por esse motivo, é difícil calcular a raiz quadrada de 3 manualmente.

Raiz quadrada de 3

Se uma calculadora for usada, pode -se ver que a raiz quadrada de 3 é 1.73205080756887…

Agora, você pode tentar manualmente aproximar esse número da seguinte maneira:

-1*1 = 1 e 2*2 = 4, isso diz que a raiz quadrada de 3 é um número entre 1 e 2.

-1,7*1.7 = 2,89 e 1,8*1,8 = 3,24, portanto, a primeira figura decimal é 7.

-1,73*1,73 = 2,99 e 1,74*1,74 = 3,02, portanto a segunda figura decimal é 3.

-1.732*1.732 = 2,99 e 1.733*1.733 = 3.003, portanto, a terceira figura decimal é 2.

E assim você pode continuar. Esta é uma maneira manual de calcular a raiz quadrada de 3.

Também existem outras técnicas muito mais avançadas, como o método Newton-Raphson, que é um método numérico para calcular aproximações.

Onde podemos encontrar o número √3?

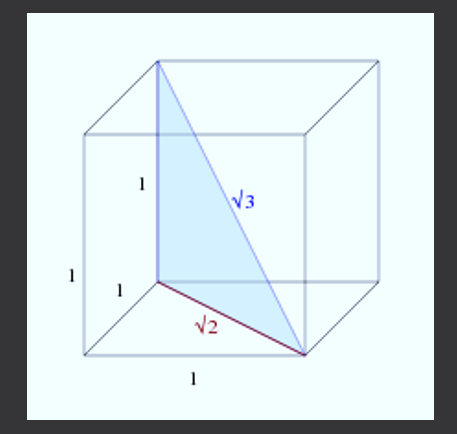
Devido ao número complicado, pode -se pensar que não aparece nos objetos do cotidiano, mas isso é falso. Se você tem um cubo (caixa quadrada), de modo que o comprimento de seus lados seja 1, as diagonais do cubo terão uma medida de √3.

Para verificar isso, é usado o teorema de Pitágoras que diz: dê.

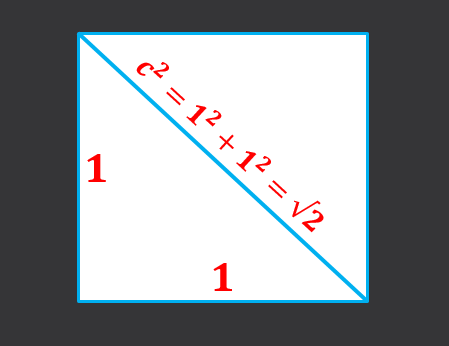
Tendo um lado do lado 1, você precisa diagonal do quadrado de sua base é igual à soma dos quadrados das categorias, ou seja, c² = 1²+1² = 2, portanto, a diagonal da medida base √2.

Agora, para calcular a diagonal do cubo, você pode ver a figura a seguir.

O novo triângulo retângulo tem pernas de comprimentos 1 e √2, portanto, ao usar o teorema de Pitágoras para calcular o comprimento de sua diagonal, é obtido: c² = 1²+(√2) ² = 1+2 = 3, é dizer , C = √3.

Assim, o comprimento da diagonal de um balde lateral 1 é igual a √3.

√3 um número irracional

No começo, foi dito que √3 é um número irracional. Para verificar isso, é assumido pelo absurdo que é um número racional, que existem dois números "A" e "B", primos relativos, como A/B = √3.

Quando a última igualdade e claro "a²", a seguinte equação é obtida: a² = 3*b². Isso diz que "a²" é um múltiplo de 3, que conclui que "a" é um múltiplo de 3.

Sendo "um" múltiplo de 3, há um número inteiro "k" tal que A = 3*K. Portanto, substituindo a segunda equação, é obtido: (3*k) ² = 9*k² = 3*b², o mesmo que b² = 3*k².

Como antes, essa última igualdade leva à conclusão de que "B" é um múltiplo de 3.

Em conclusão, "a" e "b" são múltiplos de 3, o que é uma contradição, porque a princípio foi assumido que eles eram primos relativos.

Portanto, √3 é um número irracional.