Definição de Rádio, Exemplos e Exercícios de Convergência resolvida

Ele Raio de convergência de uma série de poderes é o raio do círculo de convergência para o qual a série converge. Este círculo se estende do valor que cancela a base dos poderes para a singularidade mais próxima da função associada à série.

Toda a função analítica f (z) Ele associou uma série de poderes em torno de um ponto não escalonado, chamado Série Taylor:

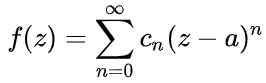
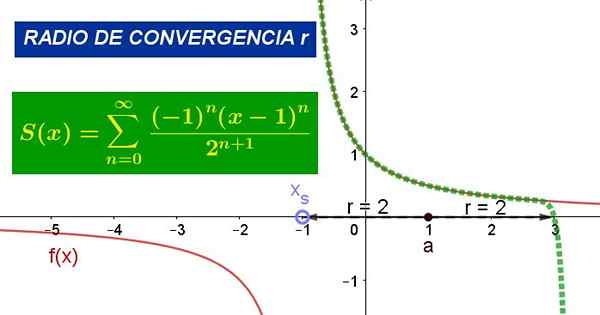
figura 1. O gráfico mostra a série de energia em torno do valor a = 1 para a função f (x). Seu raio de convergência é r = 2. Fonte: Fanny Zapata.

Onde para É o centro do círculo de convergência, z a variável independente da função e o c_n São coeficientes relacionados aos derivados da função F no ponto z = a.

O raio de convergência r É um número real positivo que define a região:

| Z - a | < r

Onde a série converge. Fora dessa região, a série divergente, ou seja, leva valores infinitos. Quando o raio de convergência é infinito, a série converge em todo o plano complexo.

[TOC]

Como o raio de convergência é determinado?

Para uma série ser convergente, é necessário que o valor absoluto dos termos sucessivos diminua quando o número de termos for muito grande. De maneira matemática, seria expresso da seguinte forma:

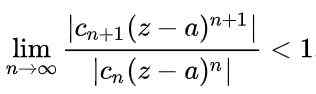
Usando as propriedades dos limites na expressão anterior, é obtido:

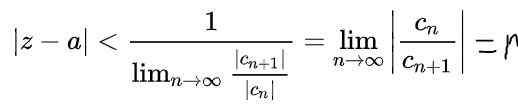
Aqui r É o raio de convergência e | Z - a | < r É o círculo de fronteira aberto no plano complexo onde a série converge. Caso o valor para e a variável z são números reais, então o intervalo aberto de convergência no eixo real será: (A - r, a+r).

Série Taylor

A série Taylor de uma função f (x) Em torno de um valor para Em que a função possui derivados infinitos, é uma série de poderes definidos como:

Pode servir a você: axiomas de probabilidade: tipos, explicação, exemplos, exercícios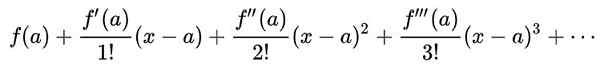

No ambiente | X - a | < r, com r comoO raio de convergência da série, a série Taylor e a função devem ser f (x) Eles coincidem.

Por outro lado, o raio de convergência r É a distância do ponto para e a singularidade x_s mais perto do ponto para, Sendo os pontos singulares, esses valores em que o limite da função tende ao infinito.

Isto é, quando x → x_s então F → ± ∞.

Exemplos

Exemplo 1

Ser S (x) Os poderes dados pela seguinte expressão:

S (x) = 1 - x + x²- x³+ x⁴-.. .+(-1)ⁿ ⋅ xⁿ +.. .

Para determinar a região em que a série converge, calculamos o quociente entre o termo (n-beeimo + 1) e o termo (n-EME):

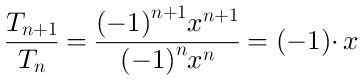
O valor absoluto do quociente anterior é | x | e seu limite quando N → ∞ também é  | x |.

Para que a série seja convergente, é necessário que:

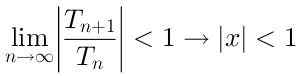
Então o raio de convergência desta série é R = 1, uma vez que converge para os valores de x que estão a uma distância menor que 1 em relação ao centro x = 0.

Exemplo 2

Você quer encontrar a série Taylor da função f (x) = 1 / (1 + x) ao redor do ponto x = 0 e determine seu raio de convergência.

Para encontrar a série, pegamos as sucessivas derivadas da função f (x), das quais mostraremos os três primeiros:

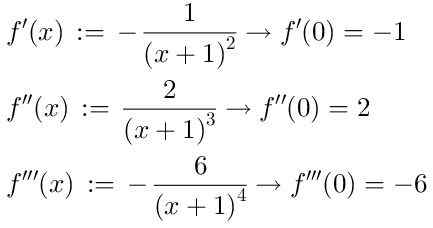
Levando em consideração que o termo de ordem zero da série Taylor é:

 f (0) = 1,

A primeira ordem: F '(0)/1!

Segunda ordem:

 F "(0)/2!

Terceira ordem:

 f "(0)/3!

E assim por diante, a série Taylor da função dada é:

f (x) = 1 - x + x² - x³ + x⁴ -.. .+(-1)ⁿ ⋅ xⁿ +.. .

Pode servir a você: Triângulo Equilateral: Características, Propriedades, Fórmulas, Área

Isso coincide com a série de poder estudada no Exemplo 1.

Já dissemos que o raio de convergência de uma série de Taylor é a distância do centro da expansão em série, que no nosso caso é o valor x = 0 até a primeira singularidade da função f (x). 

Como nossa função tem uma singularidade (ou seja, um infinito) em x = -1, A distância entre o valor -1 e o centro de expansão 0 é | -1 - 0 | = 1, Conclui -se que o raio de convergência da série Taylor é 1.

Este resultado coincide totalmente com o obtido no Exemplo 1 por outro método.

O fato de a zona de convergência da série Taylor ser o intervalo aberto (-1, 1) implica que a função e a série coincidem nesse intervalo, mas não fora do mesmo.

Isso é mostrado na Figura 2, onde 41 termos da série Taylor foram tirados, desenhados pela linha azul contínua, enquanto a função original é mostrada na linha vermelha de segmentos.

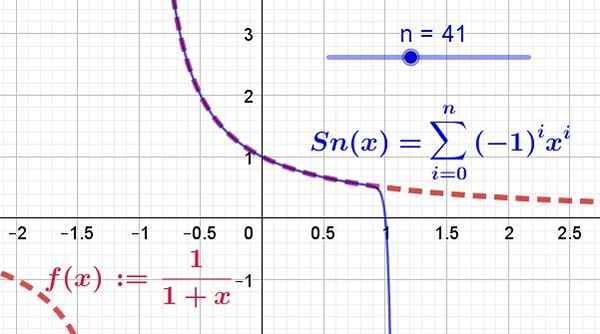Figura 2. A função f (x) (em vermelho) e sua série de poderes (ou série Taylor in Blue) são mostrados. Pode ser visto como os primeiros 41 termos da série convergem entre -1 e 1. Além disso, a função e sua série coincidem apenas na região de convergência. (Fonte: Fanny Zapata)

Exercícios resolvidos

- Exercício 1

Considere a mesma função f (x) = 1 / (1 + x) do Exemplo 2, mas desta vez é solicitado para encontrar a série Taylor da referida função em torno do ponto A = 1.

Solução

Encontramos os termos sucessivos da série, começando com o termo independente f (1) = ½.

O próximo coeficiente correspondente ao termo de primeira ordem é:

F '(1)/1! = -¼

A segunda ordem é:

F "(1)/2! = 2/(2³ 2!)

Siga o coeficiente de terceira ordem:

Pode servir você: tetradecágon

f "(1)/3! = -6 / (2⁴ 3!)

E assim por diante. A série Taylor será:

Sf (x) = ½ - 1/2² (X-1) + 1/2³(X-1)² - 1/2⁴ (X-1)³ + 1/2⁵ (X-1)⁴-..

- Exercício 2

Encontre o raio de convergência da série anterior

Solução

Escrevemos o termo n-ime e o termo n-alcaus mais um:

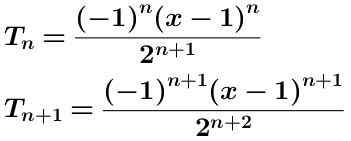Calculamos o quociente desses dois termos que são mostrados abaixo simplificados:

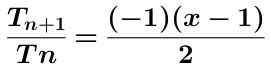
O valor absoluto da expressão anterior é obtido pela obtenção:

| X - 1 | / 2

No entanto, para que a série seja convergente, é necessário que o valor anterior seja estritamente menor que a unidade, ou seja:

| X - 1 | < 2

O que indica que o raio de convergência em torno do valor x = 1 é:

R = 1

Por outro lado, a expressão anterior é equivalente à dupla desigualdade:

-2 < x - 1 < +2

Se adicionarmos +1 a cada um dos três membros da expressão anterior, é obtido:

-1 < x < 3

Qual é o intervalo de convergência da série.

A Figura 1 mostra a função original e a série Taylor da referida função em torno do ponto x = 1. Na figura, pode -se verificar se a série coincide com a função em um ambiente de ponto x = 1, mas dentro do raio de convergência.

Referências

1. Fundação CK-12. Série de Power: Representação de Funções e Operações. Recuperado de: CK12.org.
2. Engler, a. 2019. Cálculo integral. Universidade Nacional da Costa.
3. Larson, r. 2010. Cálculo de uma variável. 9NA. Edição. McGraw Hill.
4. Textos de matemática gratuitos. Série de Power. Recuperado de: matemática.Liibretexts.org.
5. Wikipedia. Série de Power. Recuperado de: é.Wikipedia.org.
6. Wikipedia. Raio de convergência. Recuperado de: em.Wikipedia.org