O que são ângulos alternativos internos? (Com exercícios)

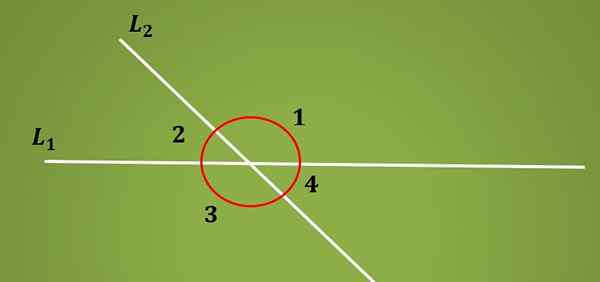
O ângulos alternativos internos São aqueles ângulos formados pela interseção de duas linhas paralelas e uma linha transversal. Quando uma linha L1 é cortada por uma linha transversal L2 4 ângulos são formados.

Os dois pares de ângulos que permanecem no mesmo lado da linha L1 são chamados de ângulos suplementares, uma vez que sua soma é igual a 180º. Na imagem inferior, os ângulos 1 e 2 são suplementares, bem como os ângulos 3 e 4.

Para falar sobre ângulos alternativos internos, é necessário ter duas linhas paralelas e uma linha transversal; Como visto antes, oito ângulos se formarão.

Quando há duas linhas paralelas L1 e L2 cortadas por uma linha transversal, oito ângulos são formados, como ilustrado na imagem a seguir.

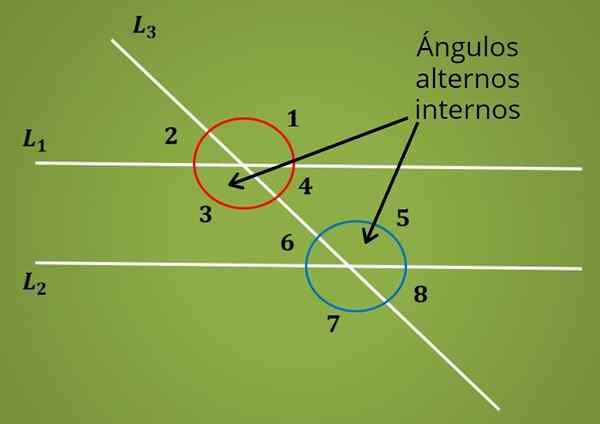
Na imagem superior, os pares de ângulos 1 e 2, 3 e 4, 5 e 6, 7 e 8 são ângulos suplementares. 

Agora, os ângulos alternativos internos são aqueles entre as duas linhas paralelas L1 e L2, mas estão localizadas nos lados opostos da linha transversal L2. Quer dizer que Os ângulos 3 e 5 são alternativos internos. Da mesma forma, os ângulos 4 e 6 são ângulos alternativos internos.

Ângulos opostos pelo vértice

Para saber a utilidade que os ângulos alternativos internos têm, é necessário saber que se dois ângulos se opuseram pelo vértice, esses dois ângulos medem o mesmo.

Por exemplo, os ângulos 1 e 3 medem o mesmo que são opostos pelo vértice. Sob o mesmo raciocínio, pode -se concluir que os ângulos 2 e 4, 5 e 7, 6 e 8 medem o mesmo.

Ângulos formados entre um secante e dois paralelos

Quando há duas linhas paralelas cortadas por uma linha seca ou transversal, como na figura anterior, é verdade que os ângulos 1 e 5, 2 e 6, 3 e 7, 4 e 8 medem o mesmo.

Ângulos alternativos internos

Usando a definição de ângulos colocados pelo vértice e a propriedade dos ângulos formados entre uma linhas secantes e duas paralelas, pode -se concluir que os ângulos alternativos internos têm a mesma medida.

Exercícios resolvidos

- Primeiro exercício

Calcule a medida do ângulo 6 da imagem a seguir, sabendo que o ângulo 1 mede 125º.

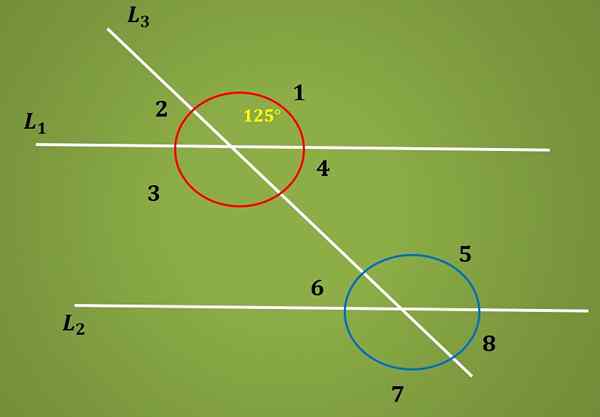
Solução

Como os ângulos 1 e 5 são opostos pelo vértice, você tem esse ângulo 3 mede 125º. Agora, como os ângulos 3 e 5 são alternados internos, você tem esse ângulo 5 também mede 125º.

Finalmente, como os ângulos 5 e 6 são suplementares, a medida do ângulo 6 é necessária é igual a 180º - 125º = 55º.

- Segundo exercício

Calcule o ângulo 3 sabendo que o ângulo 6 mede 35º.

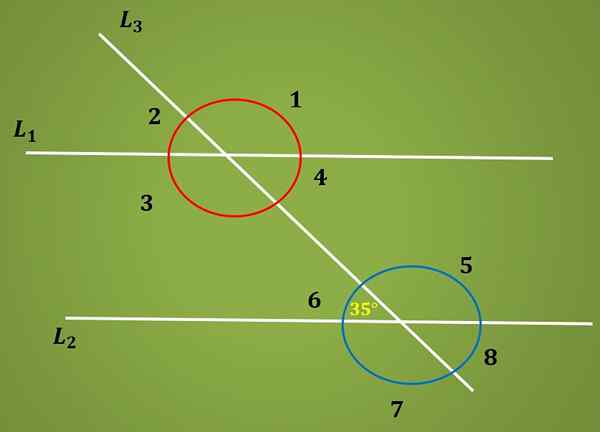
Solução

Sabe -se que o ângulo 6 mede 35º e também se sabe que os ângulos 6 e 4 são alternados internos, portanto medem o mesmo. Ou seja, que o ângulo 4 mede 35º.

Por outro lado, usando o fato de que os ângulos 4 e 3 são suplementares, a medida do ângulo 3 é igual a 180º - 35º = 145º.

Observação

É necessário que as linhas sejam paralelas para que possam atender às propriedades correspondentes.

Os exercícios podem ser resolvidos mais rapidamente, mas este artigo queria usar a propriedade de ângulos alternativos internos.

Referências

1. Bourke. (2007). Um ângulo na pasta de trabalho de matemática da geometria. Aprendizagem de NewPath.
2. Clemens, s. R., O'DAFER, p. G., & Cooney, T. J. (1998). Geometria. Pearson Education.
3. Lang, s., & Murrow, G. (1988). Geometria: um curso do ensino médio. Springer Science & Business Media.
4. Lira, a., Jaime, p., Chávez, m., Gallegos, m., & Rodríguez, C. (2006). Geometria e trigonometria. Edições de Umbral.
5. Moyano, a. R., Saro, a. R., & Ruiz, r. M. (2007). Álgebra e geometria quadrática. Netbiblo.
6. Sullivan, m. (1997). Trigonometria e geometria analítica. Pearson Education.
7. Wingard-Enelson, r. (2012). Geometria. Enslow Publishers, Inc.