Qual é a relação entre o Rhombus e a área do retângulo?

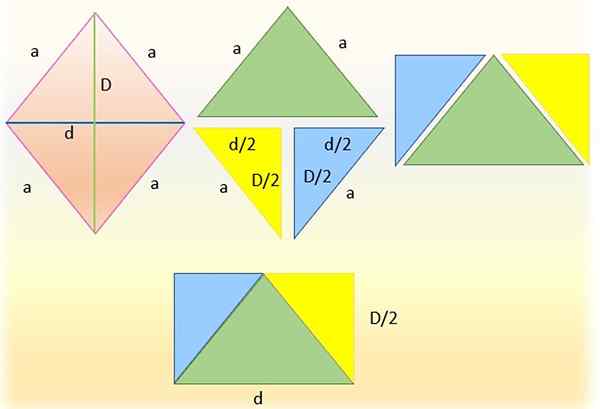
Decompondo um rombus para obter um retângulo. Fonte: f. Zapata

É possível calcular a área de Rhombus (e algumas outras figuras geométricas) da área de um triângulo ou de um quadrilátero relacionado, como um paralelograma ou um retângulo.

O retângulo e a área do paralelogramo são os mesmos: é calculado como o produto entre a base da figura e sua altura em relação a essa base. Por sua parte, a área do triângulo é o semi -produto entre sua base e sua altura.

Essas fórmulas são fáceis de lembrar, embora, naturalmente, a geometria ofereça uma fórmula exclusiva para a área de Rhombus, conhecendo a medida de suas diagonais maiores e menores, indicadas como D e D, respectivamente:

É possível deduzir essa expressão através da sequência mostrada na figura acima.

Para fazer isso, o rombus à esquerda é cortado por uma de suas diagonais, que foi feita no corte da figura pelo menor diagonal, obtendo assim dois triângulos. O triângulo superior (em verde) é deixado e o inferior é dividido por sua vez em dois triângulos, cortando pela metade da principal diagonal, obtendo os triângulos retângulos de azul e amarelo idênticos.

Então os hipotênios desses triângulos estão coincidindo com os lados do triângulo verde, pois medem o mesmo, que é "um". E um retângulo é finalmente obtido, cuja base é a diagonal "d" mais baixa e cuja altura é metade da diagonal principal, ou seja: "d/2".

A área do retângulo formada coincide exatamente a do rombus; portanto, pode -se afirmar que:

Pode atendê -lo: trinomial

PARA _diamante = (base × altura) _retângulo = D × (d/2)

Resultado que, como pode ser visto, coincide exatamente com a fórmula da área de Rhombus dada antes.

Rombo e área de paralelograma

A área de Rhombus também está relacionada à de um paralelogramo, uma vez que ambos os números geométricos são planos e pertencem à família de quadriláteros. Por exemplo, na imagem a seguir, há um rombus à esquerda e um paralelograma à direita.

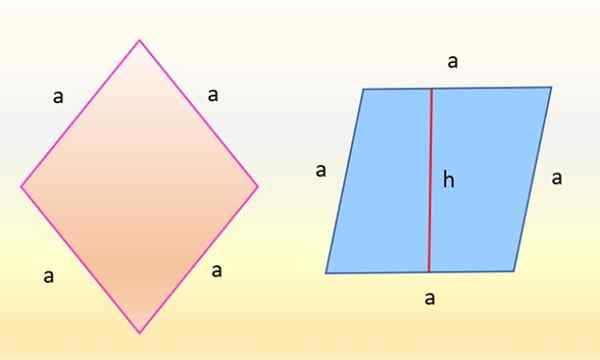A área de Rhombus à esquerda é a mesma do paralelogramo à direita. Fonte: f. Zapata

Acontece que os números são idênticos, porque o que mudou é apenas a orientação. O RHombus à esquerda, em rosa, cujos lados têm a mesma medida: A, é virado de tal maneira que um de seus lados é completamente horizontal. Então, o rombus assume a forma do paralelogramo azul à direita.

E a área deste paralelogramo também é o produto entre a base "A" e a altura em relação a essa base, chamada "H" na figura, portanto:

PARA _{paralelogramo} = A × h

Como é a mesma figura, a área é idêntica e segue que:

PARA _diamante = A × h

Assim, conhecendo e h do paralelogramo, sua área é calculada e coincidirá com o do Rhombus.

Área Rombo inscrita em um retângulo

Outra relação entre rombus e retângulo aparece quando o primeiro é registrado dentro do segundo. Se isso acontecer, os vértices do Rhombus coincidem com o ponto médio dos lados do retângulo, que é exibido abaixo:

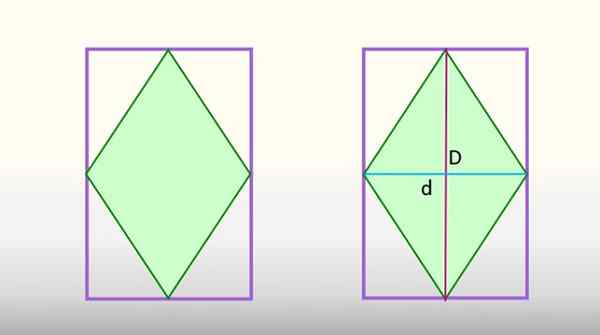A área de Rhombus inscrita no retângulo é equivalente a metade da área do retângulo. Fonte: f. Zapata

Esta disposição faz com que as diagonais maiores e menores do Rhombus, a figura é dividida em 8 triângulos idênticos, 4 dos quais correspondem ao Rhombus, em verde, e os outros 4 fazem parte do retângulo. Se esses últimos 4 triângulos se unirem, eles formariam metade do retângulo, e os 4 triângulos de Rhombus, o outro.

Pode servir a você: Isoceles Triangle

Portanto, a área de Rhombus é equivalente a metade da área do retângulo em que está registrado, afirmando que:

PARA_diamante = A_retângulo / 2

Isso é facilmente verificado calculando a área de um dos triângulos e multiplicando por 4, pois são idênticos. A área de qualquer triângulo é metade do produto entre a base e sua altura:

PARA _triângulo = base × altura /2

A partir da figura anterior, observa -se que a base de um dos triângulos é d/2 e a altura é d/2, que a substituição da fórmula anterior fornece:

PARA _triângulo = (d /2) × (d /2) /2 = (d × d) /8

Multiplicando esse resultado por 4 para ter a área de Rhombus:

PARA _diamante = 4 (d × d) /8 = (d × d) /2

Por sua parte, a metade do retângulo é:

PARA _retângulo / 2 = base × altura / 2

Como a base do retângulo é D e sua altura é D, permanece:

PARA_retângulo / 2 = d × d/ 2

Que é precisamente a área do Rhombus registrado. Conclui -se então que:

A área de um rombus registrada em um retângulo é equivalente a metade da área.

Exercícios resolvidos

Exercício 1

Quanto custa a área de Rhombus cuja principal diagonal mede 14.6 cm e a mais baixa diagonal 9.8 cm?

Solução

Substituindo d = 14.6 cm e d = 9.8 cm na fórmula da área de Rhombus:

A área procurada é:

PARA _diamante = 14.6 cm × 9.8 cm = 143.1 cm²

Exercício 2

Na figura da seção anterior, a principal diagonal do rombus registrada no retângulo mede d = 30 cm e a área do retângulo vale 210 cm². É solicitado para calcular:

a) o comprimento da diagonal menor

Pode atendê -lo: segmento de linha e semi -rio

b) A área de Rhombus, de duas maneiras: a primeira através da área do retângulo e a segunda usando a fórmula da área de um Rhombus. Verifique se o resultado é o mesmo.

Solução para

A área do retângulo é o produto entre sua base e sua altura. A maior diagonal é a sua altura, enquanto a menor diagonal D seria a base. Usando a fórmula da área e substituindo os valores da instrução, você tem:

PARA _retângulo = base × altura = d × 30 cm = 210 cm²

Então a base vale a pena:

D = 210 cm² / 30 cm = 7 cm

Solução b

Como visto acima, a área de Rhombus é metade da área do retângulo, e isso é conhecido:

PARA _diamante = 210 cm² /2 = 105 cm²

O resultado é verificado imediatamente, substituindo a fórmula:

As diagonais já são conhecidas: d = 30 cm, d = 7 cm, então:

PARA _diamante = 30 cm × 7 cm /2 = 105 cm²

Está provado que, como esperado, a área de Rhombus é a mesma nos dois casos.