O que é velocidade linear? (Com exercícios resolvidos)

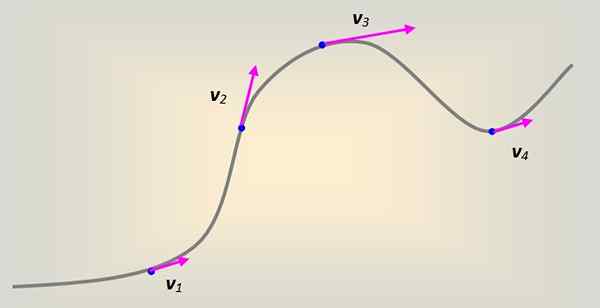
O Velocidade linear É definido como o que é sempre tangencial à trajetória seguida pela partícula, independentemente. Se a partícula sempre se mover em uma trajetória retilínea, não há problema em imaginar como o vetor de velocidade está acompanhando esta linha reta.

No entanto, em geral, o movimento é realizado em uma curva arbitrariamente. Cada parte da curva pode ser modelada como se fosse parte de um círculo de rádio para, que em todo ponto é tangente ao caminho seguido.

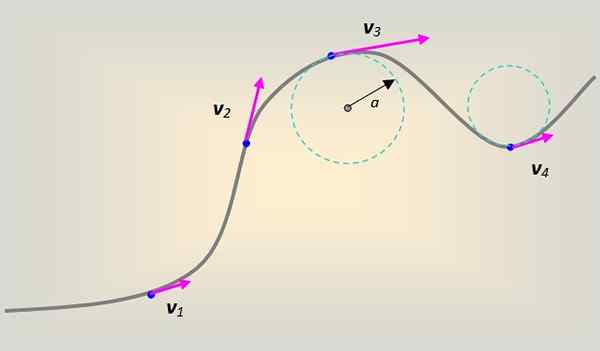figura 1. Velocidade linear em um celular que descreve uma trajetória curvilínea. Fonte: Self feito.

Nesse caso, a velocidade linear está acompanhando tangencialmente e sempre até a curva em cada ponto.

A velocidade linear matematicamente instantânea é a derivada da posição em relação ao tempo. Ser r o vetor de posição da partícula em um instante t, Então a velocidade linear é dada pela expressão:

v = r'(T) = dr / dt

Isso significa que a velocidade linear ou a velocidade tangencial, como também é chamada, nada além da mudança da posição em relação ao tempo.

[TOC]

Velocidade linear em movimento circular

Quando o movimento está em uma circunferência, podemos ir ao lado da partícula em cada ponto e ver o que acontece em duas direções muito especiais: uma delas é a que sempre aponta para o centro. Este é o endereço radial.

A outra direção importante é a que ocorre na circunferência, este é o endereço tangencial E a velocidade linear sempre tem.

Pode servir a você: pressão manométrica: explicação, fórmulas, equações, exemplos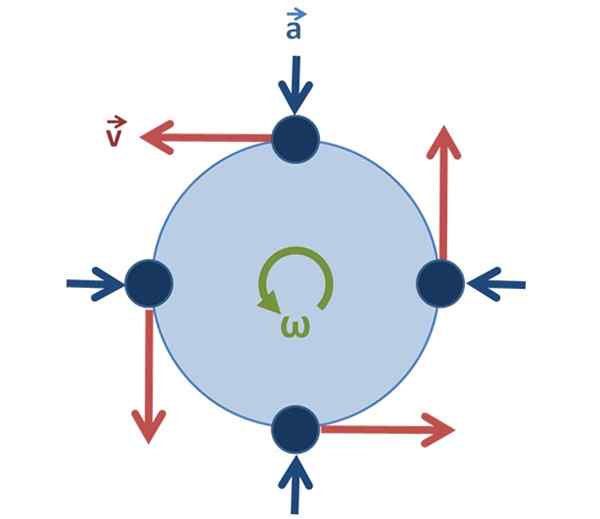Figura 2. Movimento circular uniforme: o vetor de velocidade muda de direção e direção à medida que a partícula gira, mas sua magnitude é a mesma. Fonte: Original por Usuário: Brews_ohare, Svged pelo usuário: SJLEGG [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenças/BY-SA/3.0)].

No caso do movimento circular uniforme, é importante sim, permanece inalterado.

Para este movimento, a posição em função do tempo é dada por S (t), onde s é o Tourd Arc e t é o tempo. Nesse caso, a velocidade instantânea é dada pela expressão V = ds/dt E é constante.

Se a magnitude da velocidade também varia (já sabemos que a direção sempre o faz, caso contrário, o celular não poderá girar), estamos enfrentando um movimento circular variado, durante o qual o celular, além de girar, ele pode parar ou acelerar.

Velocidade linear, velocidade angular e aceleração centrípeta

O movimento das partículas também pode ser visto do ponto de vista do ângulo varrendo, Em vez de fazer isso a partir do gol perseguido. Nesse caso, se fala do velocidade angular. Para um movimento em um círculo de rádio R, Existe uma relação entre o arco (em radianos) e o ângulo:

S = r θ

Derivando com relação a ambos os lados:

ds/dt = r (dθ/dt)

Chamando a derivada de θ em relação a t como velocidade angular E denotando -o com a letra grega ω "ômega", você tem esse relacionamento:

v = ωR

Aceleração centrípeta

Todo movimento circular tem aceleração centrípeta, isso é sempre direcionado para o centro da circunferência. Ela tome cuidado para que a velocidade esteja mudando para se mover com a partícula quando ela se vira.

Pode servir a você: Curva de calibração: para que é, como fazer isso, exemplos

Aceleração centrípeta para_c qualquer para_R Ele sempre aponta para o centro (veja a Figura 2) e está relacionado à velocidade linear dessa maneira:

para_c = v² /R

E com velocidade angular como:

para_c = (ΩR)² /R = ω²R

Para um movimento circular uniforme, a posição S (t) É da forma:

S (t) = SO+ VT

Além disso, o movimento circular variado deve ter um componente da aceleração chamada Aceleração tangencial para_T, que lida com a mudança da magnitude da velocidade linear. Sim para_T  é constante, A posição é:

S (t) = s_qualquer + v_qualquerT + ½ A_Tt²

Com v_qualquer Como a velocidade inicial.

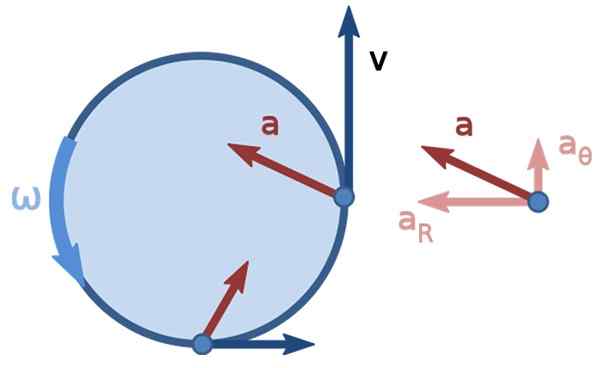Figura 3. Movimento circular não uniforme. Fonte: nãouniform_circular_motion.PNG: Brews Ocharedorivative Work: Kooning Jons [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenças/BY-SA/3.0)].

Exercícios de velocidade linear resolvidos

Os exercícios resolvidos contribuem para esclarecer o uso adequado dos conceitos e equações fornecidas.

-Exercício resolvido 1 

Um inseto se move em um raio semicírculo r = 2 m, começando de repouso no ponto um tempo aumentando sua velocidade linear, a uma taxa de p m/s². Encontre: a) Após que horas atinge o ponto B, b) o vetor de velocidade linear naquele momento, c) a aceleração do vetor naquele momento.

Figura 4. Um inseto começa em A e atinge B em uma trajetória semicircular. Tem uma velocidade linear. Fonte: Self feito.

Solução

a) A declaração indica que a aceleração tangencial é constante e vale π m/s², Em seguida, é válido usar a equação para movimento uniformemente variado:

S (t) = s_qualquer + v_qualquerT + ½ A_T.t²

Com s_qualquer = 0 e V_qualquer = 0:

S (t) = ½ a_T.t²

S = πR (Metade do comprimento da circunferência)

T = (2. πR /para_T) ^½ S = (2π.2 /π)^½S = 2 s

b) v (t) = V_qualquer + para_T. T = 2π EM

Quando no ponto B, o vetor de velocidade linear aponta na direção vertical para baixo na direção (-e):

Pode atendê -lo: qual é a constante dielétrica?

v (t) = 2π EM(-e)

c) Falta aceleração tangencial, a aceleração centrípeta está faltando para ter o vetor de velocidade para:

para_c = v² / R = (2π)² / 2 m/ s² = 2π² EM²

para = a_c (-x) + a_T (-e) = 2π²(-x)+ π (-e) EM²

-Exercício resolvido 2

Uma partícula gira em um círculo de rádio 2.90 m. Em um determinado momento, sua aceleração vale 1.05 m/s² em uma direção que forma 32 com sua direção de movimento. Encontre sua velocidade linear em: a) neste momento, b) 2 segundos depois, assumindo que a aceleração tangencial é constante.

Solução

a) A Diretoria de Movimento é precisamente o endereço tangencial:

para_T = 1.05 m/s² . cos 32º = 0.89 m/s² ; para_C = 1.05 m/s² . Sen 32º = 0.56 m/s²

A velocidade limpa de para_c = v² / R como:

v = (r.para_c)^1/2  = 1.27 m/s

b) A equação para movimento uniformemente variado é válido da seguinte maneira: v = v_qualquer + para_TT = 1.27 + 0.89 .2² m/s = 4.83 m/s

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill. 84-88.
2. Figueroa, d. Série física para ciência e engenharia. Volume 3. Edição. Cinemática. 199-232.
3. Giancoli, d.  2006. Física: Princípios com aplicações. 6^º… Ed Prentice Hall. 62-64.
4. Movimento relativo. Recuperado de: cursos.Lumenarning.com
5. Wilson, J. 2011. Física 10. Pearson Education. 166-168.