O que é reatância capacitiva e como calculá -la?

O reatância capacitiva É a resistência que um condensador, um elemento regulatório do fluxo de carga em um circuito de corrente alternado, se opõe à passagem da corrente.

Em um circuito constituído de um condensador e ativado por uma fonte de corrente alternada, a reatância capacitiva x pode ser definida_C da seguinte maneira:

X_C = 1 / ωc

figura 1. Reatâncias capacitivas fazem parte dos filtros Passabajos e falantes de palestrantes. Fonte: Pixabay.

Ou também:

X_C = 1 / 2πfc

Onde C é a capacidade do capacitor e ω é a frequência angular da fonte, relacionada à frequência f através:

Ω = 2πf

A reatância capacitiva depende do inverso da frequência; portanto, em altas frequências tende a ser pequenas, enquanto em baixas frequências, a reatância é grande.

A unidade do sistema internacional para medir a reatância capacitiva é o ohm (ω), desde que a capacidade do capacitor esteja em Farad (abreviada F) e a frequência seja expressa no inverso dos segundos (S^-1).

Enquanto a carga dura, uma tensão e uma corrente também são estabelecidas através do capacitor, cujas amplitudes ou valores máximos, denotados respectivamente como V_C e eu_C, Eles estão relacionados através da reatância capacitiva análoga à lei de Ohm:

V_C = I_C ⋅ x_C

Em um condensador, a tensão é atrasada 90º em relação à corrente, ou é avançado 90º em relação a isso, como preferido. De qualquer forma, a frequência é a mesma.

Quando x_C É muito grande, a corrente tende a ser pequena e fazer o valor de x infinito_C, O condensador se comporta como um circuito aberto e a corrente é zero.

[TOC]

Como calcular a reatância capacitiva

Vejamos um exemplo de como calcular a reatância capacitiva: suponha que um capacitor de 6 μF esteja conectado a uma tomada alternada e frequência e frequência F 60 Hz.

Para encontrar a reatância capacitiva, a definição dada no início é usada. A frequência angular ω é dada por:

Pode servir a você: Indução magnética: fórmulas, como é calculado e exemplos

Ω = 2πf = 2π x 60 Hz = 377 s^-1

Então este resultado é substituído na definição:

X_C = 1 / ωc = 1 / (377 s^-1x 6 x10 ^-6 F) = 442.1 ohm

Agora vamos ver a amplitude da corrente circulando no circuito. Como a fonte oferece uma tensão de amplitude V_C = 40 V, usamos a relação entre reatância capacitiva, corrente e tensão para calcular a amplitude da corrente ou corrente máxima:

Yo_C = V_C / X_C = 40 v / 442.1 ohm = 0.09047 a = 90.5 m a.

Se a frequência se tornar muito grande, a reatância capacitiva se tornará pequena, mas se a frequência se tornasse 0 e tivemos uma corrente direta, a reatância tenderia a ser infinita.

Tensão atual e condensadora

Quando um condensador se conecta a uma fonte de corrente alternada, como oscila e altera sua polaridade, o capacitor experimenta cargas e descarrega alternadamente.

Para uma frequência de 60 Hz como o exemplo, a tensão é positiva 60 vezes por segundo e negativo outras 60 vezes por segundo.

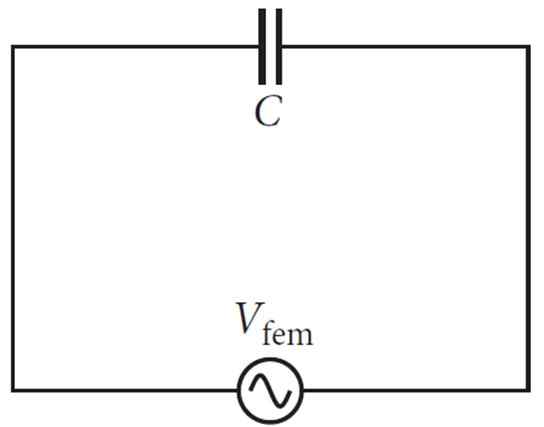
Figura 2. Circuito simples do condensador e fonte de corrente alternada. Fonte: f. Zapata.

Ao aumentar a tensão, ele impulsiona a corrente em uma direção, mas se o condensador estiver baixando, ocorre a corrente na direção oposta que se opõe ao primeiro.

Sim v_C (t) = V_m Sen ωt, sabendo que a capacidade é a razão entre a carga e a tensão, teremos a carga:

C = Q/V → Q (t) = CV = CV_m Sen ωt

E tendo a carga dependendo do tempo, teremos a corrente, que é a derivada disso:

Yo_C(t) = CV_m Ω cos ωt

Mas mama e cosseno estão relacionados através de: cos α = sin (α + π/2), portanto:

Yo_C(t) = CV_m Ω sen (ωt + π/2) = i_C Sen (ωt + π/2)

Com i_C = Cv_C Ω

Como pode ser visto, há uma diferença de 90º avanço da corrente em relação à tensão, conforme comentado no começo.

Pode servir a você: Millikan Experiment: Procedimento, Explicação, Importância

Na descrição desse tipo de circuitos, o conceito de Fasor, que se parece muito com um vetor e permite representar no plano complexo qualquer quantidade alternada, como corrente, tensão ou impedância.

A figura a seguir mostra, à direita, a tensão e os fasores de corrente no capacitor, que formam um ângulo de 90º, que é o atraso entre os dois.

À esquerda estão os respectivos gráficos, de diferentes amplitudes, mas igual frequência. Com o tempo, os avanços atuais para a tensão e quando isso é máximo, a corrente é zero e quando a tensão é zero, a corrente é máxima, mas com a polaridade invertida.

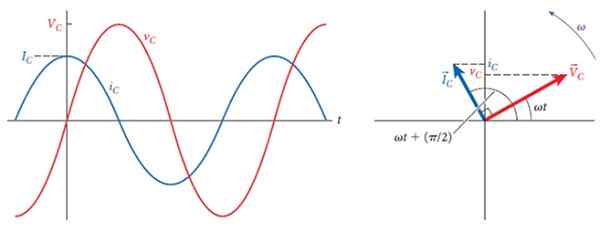Figura 3. 90º atraso entre a corrente e a tensão através de um capacitor. Fonte: Bauer, W.

Impedância complexa do condensador

Em um circuito com resistências, capacitores e indutâncias, a reatância é a parte imaginária da impedância Z, uma quantidade complexa de que, em circuitos de corrente alternados, tem um papel semelhante ao da resistência elétrica para a corrente direta da corrente direta.

De fato, a impedância de um circuito é definida como a razão entre a tensão e a corrente:

Z = v / i

Para um capacitor ou capacitor, sua impedância é dada pelo quociente:

Z_C = V (t) / i (t) = V_C Sen ωt / i_C Sen (ωt + π/2)

Uma maneira de expressar tensão e corrente como fasores é indicar a amplitude e o ângulo de fase (forma polar):

v (t) = V_C 0º 0º

Eu (t) = eu_C 90º

Portanto:

Z_C = V_C 3 0º / i_C 3 90º = (V_C / Yo_C) Ero 0º -90º =

= V_C / CV_C Ω porte -90º = (1/ ωc) porte -90º = =

Z_C = (- j) x_C

Isto é, a impedância do condensador é sua reatância capacitiva multiplicada pelo negativo da unidade imaginária.

Impedância de um circuito RC em série

A impedância de um circuito de corrente alternado com resistência, capacitores e indutores também pode ser representado binomialmente por:

Pode servir a você: Primeira Lei da Termodinâmica: Fórmulas, Equações, Exemplos

Z = r + jx

Nesta equação, r representa a resistência, que corresponde à parte real, J é a unidade imaginária e x é a reatância, que pode ser capacitiva ou indutiva ou combinação de ambos, se esses elementos estiverem presentes ao mesmo tempo no circuito.

Se o circuito contiver uma resistência e um capacitor em série, sua impedância é:

Z = z_R + Z_C    

Como na tensão e corrente de resistência estão em fase, a impedância resistiva é simplesmente o valor da resistência r.

No caso de impedância capacitiva, já vimos que Z_C = -Jx_C , Portanto, a impedância do circuito RC é:

Z = r - jx_C = R - j (1/ ωc)

Por exemplo, no circuito mostrado abaixo, cuja fonte é da forma:

100 V ⋅ sen (120πt)

Observando que ω = 120π, a impedância é:

Z = 83.0 - J [(1 / (120π ⋅ 6 x 10^-6)] Ohm = 83.0 - 442.1 J ohm.

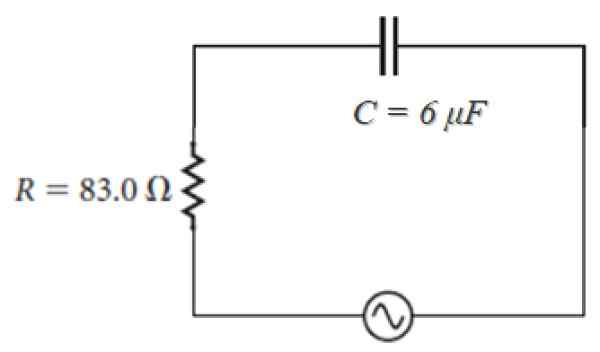Figura 4. Série de circuitos RC com fonte de corrente alternada. Fonte: f. Zapata.

Aplicações de reatância capacitivas

Filtros altos da PASA, filtros de passes baixos, circuitos de ponte para medir capacitâncias e indutâncias e circuitos da geladeira estão entre as principais aplicações de circuito que contêm reatâncias capacitivas, em combinação com indutâncias e resistência elétrica.

Em equipamentos de som, alguns alto -falantes vêm com tipos separados de tipo Woofer (maior) para baixas frequências e Tweeter ou chifre pequeno para altas frequências. Dessa maneira, o desempenho e a qualidade do áudio melhoram.

Eles são capacitores usados ​​que impedem a chegada de baixas frequências no tweeter, enquanto um indutor é adicionado no woofer para evitar sinais de alta frequência, uma vez que a indutância tem uma reatância proporcional à frequência: x x x_eu = 2πfl.

Referências

1. Alexander, c. 2006. Fundações de circuito elétrico. 3º. Edição. Mc Graw Hill.
2. Bauer, w. 2011. Física para engenharia e ciências. Volume 2. Mc Graw Hill.
3. Figueroa, d. 2005. Série: Física para Ciência e Engenharia. Volume 6. Eletromagnetismo. Editado por Douglas Figueroa (USB).
4. Giancoli, d.  2006. Física: Princípios com aplicações. 6º. Ed Prentice Hall.
5. Serway, r., Jewett, J. 2008. Física para Ciência e Engenharia. Volume 1. 7º. Ed. Cengage Learning.