Qual é o momento magnético?

Ele Momento magnético É um vetor que relaciona a corrente que cruza um pouco ou fechada com a área do mesmo. Seu módulo é igual ao produto da intensidade da corrente pela área, e sua direção e direção são dadas pela regra da mão direita, como mostra a Figura 1.

Esta definição é válida independentemente. Quanto à unidade do momento magnético, no sistema internacional de unidades, se for ampere × m².

figura 1. O vetor de momento magnético de um título de corrente arbitrária é perpendicular ao seu plano e a direção é determinada pela regra do polegar direito. Fonte: Wikimedia Commons.

Em termos matemáticos, denotando o momento magnético do vetor com as letras gregas μ (Em negrito porque é um vetor e, portanto, se distingue de sua magnitude), é expresso como:

μ = I a n

Onde eu é a intensidade da corrente, a é a área que envolve o loop e n É o vetor da unidade (do módulo igual a 1) que aponta na direção perpendicular ao plano da SPASE e cujo significado é dado pela regra do polegar direito (veja a Figura 1).

Esta regra é muito simples: enrolando os quatro dedos da mão direita para que eles sigam a corrente, o polegar indica direção e direção de n e, portanto, o momento magnético.

A equação anterior é válida para um loop. Se houver nougas como em uma bobina, o momento magnético é multiplicado por n:

μ = nI a n

[TOC]

Momento magnético e campo magnético

É fácil encontrar expressões para o momento magnético de turnos com formas geométricas regulares:

-Lado quadrado do lado ℓ: μ = Euℓ² n

-Lados em espiral retangular para e b: μ = IAB n

-Rádio R. Radio Spira: μ = Iπr² n

Pode atendê -lo: número atômico

Campo magnético de Dipolo

O campo magnético produzido pelo circuito ou espásea atual se assemelha ao de um ímã de barra e também do da terra.

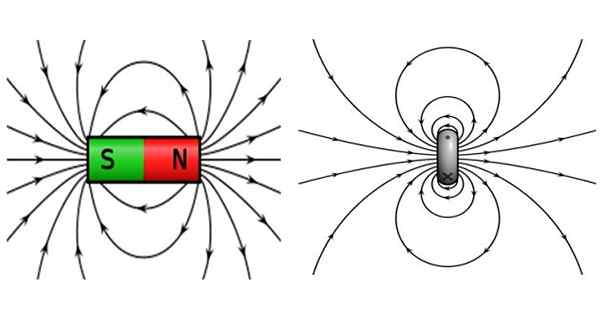Figura 2. À esquerda, o campo magnético de um ímã de barra e à direita que produz uma espiral circular que transporta corrente. Fonte: Wikimedia Commons.

Os ímãs de barra são caracterizados por ter o Pólo Norte e o Pólo Sul, onde pólos opostos são atraídos e os mesmos postes repelem. As linhas de campo estão fechadas, deixe o Pólo Norte e alcance o Pólo Sul.

Agora, os pólos magnéticos são inseparáveis, o que significa que, se um ímã de barra for dividido em dois ímãs menores, eles continuam a ter seus próprios postes norte e sul. Não é possível ter os pólos magnéticos isolados, e é por isso que o ímã da barra é chamado Dipolo magnético.

O campo magnético de um raio R Spiral R, que transporta um Inte. Para os pontos pertencentes ao seu eixo de simetria (neste caso o eixo X), o campo é dado por:

Onde μ_qualquer É a permeabilidade do vácuo. Levando o campo em pontos de distância da SPASE, para a qual é cumprido que x >> r, o campo se aproxima:

Relação entre o campo magnético e o momento magnético do dipolo

Incluindo o momento magnético na expressão anterior é:

Dessa maneira, a intensidade do campo magnético é proporcional ao momento magnético. Observe que a intensidade do campo diminui com o cubo de distância.

Esta abordagem é aplicável a qualquer loop, desde que x ser grande em comparação com suas dimensões.

E como as linhas deste campo se assemelham às do ímã da barra, a equação é um bom modelo para este campo magnético e de outros sistemas cujas linhas são semelhantes, como: por exemplo:

Pode atendê -lo: absorvância: o que é, exemplos e exercícios resolvidos

-Partículas carregadas em movimento como o elétron.

-O átomo.

-Terra e outros planetas e satélites do sistema solar.

-Estrelas.

Efeito de um campo externo no loop

Uma característica muito importante do momento magnético é o seu link para o torque que a experiência da alça na presença de um campo magnético externo.

Um motor elétrico contém bobinas pelas quais um fluxo de mudança de direção está passando e que graças ao campo externo experimenta um efeito de turno. Este turno faz com que um eixo se mova e a energia elétrica se torne energia mecânica durante o processo.

Torque em um loop retangular

Suponha, para facilitar os cálculos, lados retangulares para e b, cujo vetor normal n, tela de saída, inicialmente é perpendicular a um campo magnético uniforme B, Como na Figura 3. Os lados da experiência de loop forças dadas por:

F = Ieu x B

Onde eu É um vetor de magnitude igual ao comprimento do segmento e direcionado de acordo com a corrente, e é a intensidade do mesmo e B É o campo. Força é perpendicular a ambos eu Como o campo, mas nem todos os lados experimentam força.

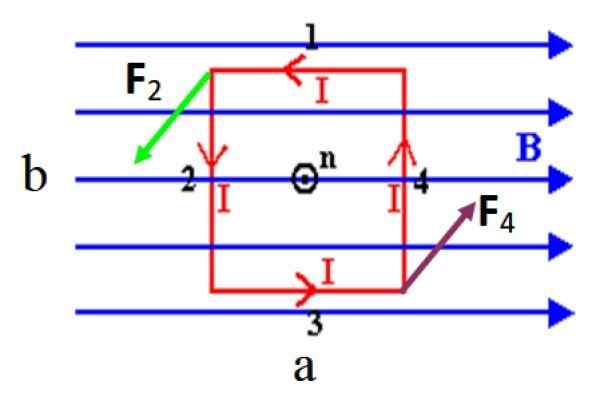Figura 3. Uma espiral retangular que transporta uma corrente I em um sentido anti -hemearário, experimenta um torque na presença de um campo magnético uniforme uniforme. Fonte: f. Zapata.

Na figura mostrada, não há força nos lados curtos 1 e 3 por ser paralelo ao campo, lembre -se de que o produto cruzado entre vetores paralelos é anulado. No entanto, lados longos 2 e 4, que são perpendiculares a B, eles experimentam forças denotadas como F₂ e F₄.

Essas forças se formam um par: Eles têm a mesma magnitude e direção, mas os sentidos opostos, portanto não são capazes de se mover para o loop no meio do campo. Mas eles podem fazê -lo girar, já que o torque  τ Que cada força exerce, com relação ao eixo vertical que passa pelo centro do loop, ele tem a mesma direção e significado.

Pode atendê -lo: força de coesão

De acordo com a definição de torque, onde r É o vetor de posição:

τ = r x F

Então:

τ₂ = τ₄=(A/2) F (+J )

Torques individuais não são cancelados, pois têm a mesma direção e significado, são adicionados:

τ_líquido = τ₂ + τ₄ = A F (+J )

E sendo a magnitude da força f = ibb, isso resulta:

τ_líquido = IoLa avác+J )

O produto A avice é a área A da SPASE, então IAB é a magnitude do momento magnético μ. Portanto τ_líquido = μ⋅b (+J )

Pode -se observar que, em geral, o torque coincide com o produto vetorial entre os vetores μ e B:

τ_líquido = μ x B

E embora essa expressão tenha sido derivada de um loop retangular, é válido para uma posição plana arbitrariamente.

O efeito do campo no loop é um torque que tende a alinhar o momento magnético com o campo.

Energia potencial do dipolo magnético

Para virar a espiral ou o dipolo no meio do campo, uma obra deve ser realizada contra a força magnética, o que muda a energia potencial de dipolo. A variação da energia Δu, quando a espiral gira do ângulo θ_qualquer No ângulo θ é dado pela integral:

Se o nível de referência for escolhido como θ_qualquer = π/2:

Δu = -μb cos θ

Que por sua vez podem ser expressos como o produto escalar entre os vetores B e μ:

ΔU = - μ ·B

A energia potencial mínima no dipolo ocorre quando cos θ = 1, o que significa que μ e B Eles são paralelos, a energia é máxima se for oposta (θ = π) e é nula quando são perpendiculares (θ = π/2).

Referências

1. Figueroa, d. 2005. Série: Física para Ciência e Engenharia. Volume 5. Eletromagnetismo. Editado por Douglas Figueroa (USB).
2. Resnick, r. 1999. Físico. Vol. 2. 3ª ed. em espanhol. Empresa Editorial Continental S.PARA. claro.V.
3. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 2. Pearson.
4. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 2. 7º. Ed. Cengage Learning.
5. Tipler, p. (2006) Física para ciência e tecnologia. 5ª ed. Volume 2. Editorial revertido.