Qual é o módulo de corte, rigidez ou cisalhamento? (Exercícios resolvidos)

Ele Módulo de corte Descreva a resposta de um material à aplicação de um esforço de cisalhamento que o deforma. Outras denominações frequentes de uso para o módulo de corte são cisalhamentos, tesouras, elasticidade transversal ou módulo de elasticidade tangencial.

Quando os esforços são pequenos, as deformações são proporcionais a elas, de acordo com a lei de Hooke, a constante de corte sendo a proporcionalidade constante. Portanto:

Módulo de corte = esforço de corte/deformação

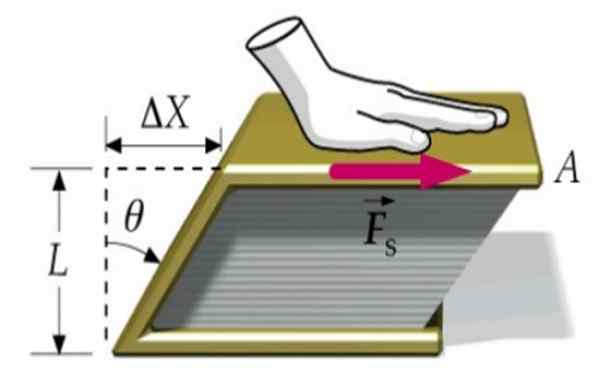
figura 1. Um livro é deformado graças à força tangencial FS. Fonte: f. Zapata.

Suponha que uma força seja aplicada na tampa de um livro, sendo o outro fixado na superfície da tabela. Dessa maneira, o livro como um todo não se move, mas se deforma quando a tampa superior se move em relação à inferior na quantidade Δx.

O livro vai de ter uma seção transversal retangular para uma seção na forma de paralelogramo, como vemos na imagem superior.

Ser:

τ = f/a

O esforço ou tensão de corte, sendo F a magnitude da força aplicada e PARA A área em que age.

A deformação causada é dada pelo quociente:

Δ = Δx / L

Portanto, o módulo de corte, que indicaremos como G, é:

Dessa maneira, o módulo de corte é responsável por medir a resistência dos planos internos do objeto que são paralelos ao esforço aplicado.

E como Δx / l carece de dimensões, as unidades de g são as mesmas que as do esforço de corte, que é a razão entre a força e a área.

No sistema internacional de unidades, essas unidades são Newton/metro quadrado ou Pascal, PA abreviado. E nas unidades anglo -saxon é libra /polegada quadrada, abreviada psi.

[TOC]

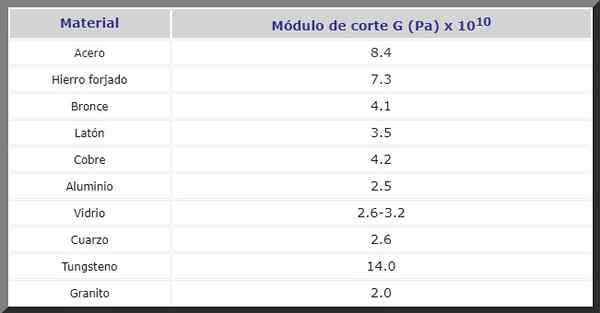
Pode servir a você: movimento retilíneo uniforme: características, fórmulas, exercícios

Módulo de corte para vários materiais

Sob a ação das forças de corte como as descritas, os objetos oferecem uma resistência semelhante à do livro, no qual as camadas interiores deslizam. Esse tipo de deformação só pode ocorrer em corpos sólidos, que têm rigidez suficiente para se opor a ser deformado.

Por outro lado, os líquidos não oferecem esse tipo de resistência, mas podem experimentar deformações de volume.

Figura 2. Os parafusos em estruturas estão sujeitos a esforços de corte. Fonte: Pixnio.

Em seguida, você tem o módulo G -CUT em P para vários materiais freqüentemente usados ​​em construção e na fabricação de máquinas e partes de reposição de todos os tipos:

Medida experimental do módulo de corte

Para encontrar o valor do módulo de corte, você deve testar amostras de cada material e examinar sua resposta à aplicação de um esforço de corte.

A amostra é uma haste feita com o material, com rádio R e comprimento eu conhecido, que é fixo em uma extremidade, enquanto o outro se conecta ao eixo de uma polia livre.

A polia tem uma corda amarrada, na parte de cuja extremidade livre é pendurada que exerce uma força F Na vara através da corda. E essa força, por sua vez, produz um momento M Na haste, que então transforma um pequeno ângulo θ.

Um esquema de montagem pode ser visto na figura a seguir:

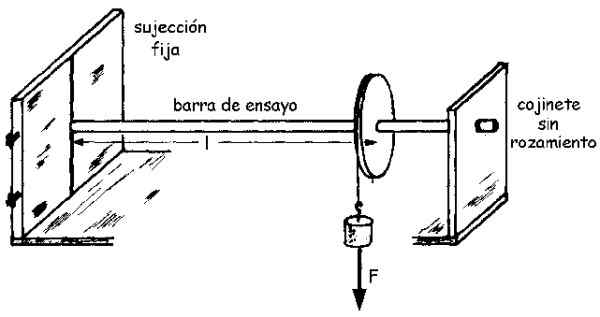Figura 3.- Conjunto experimental para determinar o módulo de cisalhamento ou corte de uma barra de teste fina. Fonte: Universidade de Valladolid.

A magnitude do momento M, que denotamos como M (sem negrito) está relacionado ao ângulo girado θ através do módulo de corte G de acordo com a seguinte equação (é deduzida por uma integral simples):

Como a magnitude do momento é igual ao produto do módulo Force F pelo raio da polia r_p:

Pode servir a você: Torricelli Experimento: medidas de pressão atmosférica, importância

M = f.R_p

E força é o peso que pendura C, então:

M = w.R_p

Substituindo na equação da magnitude do momento:

Você tem a relação entre peso e ângulo:

Como encontrar g?

Essa relação entre variáveis C e θ É linear, então os diferentes ângulos produzidos pendurados diferentes pesos são medidos.

Os casais de peso e ângulo são gráficos em um papel de milímetro, a melhor linha que passa pelos pontos experimentais é ajustada e a inclinação é calculada m da referida linha.

 A partir daí, segue -se:

Exercícios com solução

- Exercício 1

Uma haste de 2.5 metros de comprimento e rádio 4.5 mm é consertado em uma extremidade. O outro se conecta a uma polia de rádio de 75 cm que tem um peso 1 1.3 kg. O ângulo virado é 9.5 ª.

Com esses dados, é solicitado para calcular o módulo de corte g da haste.

Solução

Da equação:

Gasses G:

E os valores fornecidos na declaração são substituídos, tomando cuidado para expressar todos os dados no sistema internacional de unidades se:

R = 4.5 mm = 4.5 x 10 ^-3 m

R_p = 75 cm = 0.075

Passar de quilogramas (na verdade são quilogramas - força) para Newton multiplica por 9.8:

W = 1.3 kg-force = 1.3 x 9.8 n = 12.74 n

E, finalmente, os diplomas devem estar em radianos:

9.5th = 9.5 x2π /360 radianos = 0.1658 Radianes.

Com tudo isso que você tem:

= 2.237 x 10¹⁰ PA

- Exercício 2

Um cubo de gel é de 30 cm. Um de seus rostos é fixo, mas, ao mesmo tempo, uma força paralela de 1 N é aplicada à face oposta, que graças a isso se move 1 cm (veja o exemplo do livro na Figura 1).

Pode servir a você: Magnetização: Orbital e Moment Magnético, Exemplos

É solicitado a calcular com estes dados:

a) A magnitude do estresse de cisalhamento

b) deformação unitária δ

c) o valor do módulo de corte

Solução para

A magnitude do estresse de cisalhamento é:

τ = f/a

Com:

A = lado² = (30 x 10^-2 cm)² = 0.09 m²

Portanto:

τ = 1 n / 0.09 m² = 11.1 PA

Solução b

A deformação unitária não é outra senão o valor de δ, dado por:

Δ = Δx / L

O deslocamento da face submetido à força é de 1 cm, então:

Δ = 1/30 = 0.0333

Solução c

O módulo de corte e o quociente entre o esforço de corte e a deformação da unidade:

G = esforço de corte/deformação

Portanto:

G = 11.1 pa /0.033 = 336.4 PA

Referências

1. Cerveja, f. 2010. Mecânica de Materiais. McGraw Hill. 5 ª. Edição.
2. Franco Garcia, para. Sólido rígido. Ouça a medição do módulo. Recuperado de: SC.Ehu.é.
3. Giancoli, d.  2006. Física: Princípios com aplicações. 6º. Ed Prentice Hall.
4. Resnick, r. (1999). Físico. Vol. 1. 3ª ed. em espanhol. Empresa Editorial Continental S.PARA. claro.V.
5. Universidade de Valladolid. Departamento de Física da matéria condensada. Seleção de problemas. Recuperado de: www4.uva.é.