Proporção

Uma proporção é a relação de igualdade que existe entre duas razões. Faz parte do todo. Shuttersock

O que é uma proporção?

Quando falar sobre proporção Nos referimos a uma parte, uma quantidade ou um componente considerado em relação a todo o que é parte.

Por exemplo, se queremos esculpir uma escultura que representa um corpo humano de tamanho natural, todas as partes devem estar em proporção, ou seja, elas não devem ser menores ou maiores do que o que corresponde à figura humana.

Se queremos preparar uma boa paella, devemos cuidar da proporção entre a quantidade de arroz e água, mariscos e barragens de coelho, para que não haja excesso ou falta de nenhuma das três quantidades.

A proporção em matemática

Em matemática, há falar de proporção ou proporcionalidade quando dois ou mais números mantêm uma razão constante entre si.

Vejamos as seguintes frações:

2/4 - 4/8 - 8/16

À primeira vista, poderíamos ter a impressão de que eles representam números completamente diferentes, pois diferentes são os três numeradores e os três denominadores entre si.

Mas se o numerador for dividido entre o denominador, verificaremos que o resultado é o mesmo nas três frações: 0,5.

Se observarmos um pouco mais, veremos que a segunda fração da série foi obtida multiplicando por 2 a primeira fração; E o terceiro, por sua vez, é o produto de multiplicar por dois a segunda fração:

2/4 x 2/2 = 4/8 -4/8 x 2/2 = 8/16

Assim, as três frações representam o mesmo quociente (0,5) e são separadas pelo mesmo motivo (2). É por isso que podemos dizer que eles são proporcionais.

Pode atendê -lo: Pentadecágono: elementos, classificação, características, exercício

A primeira e a terceira equação da série também são proporcionais entre si, mas em uma proporção de 4:

2/4 x 4/4 = 8/16

Tipos de proporções

As proporções podem ser de vários tipos, a saber::

Proporção direta

Estamos enfrentando esse tipo quando, aumentando uma das quantidades da proporção, o outro também aumenta e vice -versa: se uma quantidade diminuir, o mesmo acontecerá com o outro.

Por exemplo, vamos pensar na distância que um carro percorre em duas horas que se move a 100 km/h. A resposta é de 200 quilômetros.

Vamos agora aumentar sua velocidade: não vai mais passar para 100, mas 150 km/h. Quanta distância terá percorrido depois de duas horas? 300 quilômetros.

Assim, aumentando a velocidade também aumenta a distância percorrida em um certo período de tempo. Ambos os elementos estão em proporção direta.

Proporção inversa

Nesse caso, aumentando o primeiro mandato da proporção, o segundo diminui e vice -versa: se o segundo for aumentado, o primeiro termo diminui.

Vamos voltar ao exemplo do carro, mas desta vez vamos nos perguntar: quanto tempo leva para percorrer uma distância de 100 quilômetros por carro que se move a 100 km/h? Obviamente, uma hora.

Agora vamos acelerar. O veículo atinge 200 km/h. Quanto tempo levará para viajar os mesmos 100 quilômetros? A resposta é de 0,5 horas ou 30 minutos.

Como vemos, aumentando a velocidade, o tempo que o veículo precisa para cobrir a distância é reduzido. Velocidade e tempo são, portanto, em relação reversa proporcional.

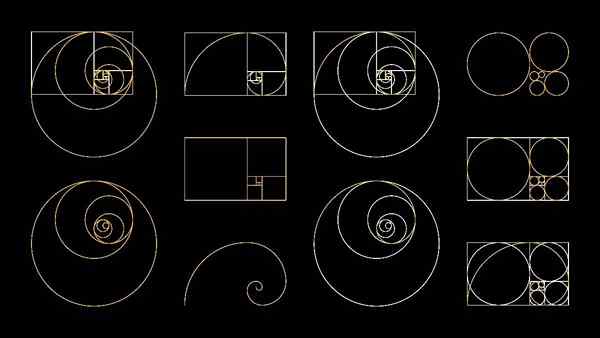
Proporção de aurea

Também conhecido como a razão dourada, número dourado ou proporção divina, é um número irracional, ou seja, não pode ser representado por uma fração, pois possui decimais não periódicos infinitos.

Pode atendê -lo: múltiplos de 2: o que são e explicação

Este número, já descoberto na antiguidade e simbolizou com a letra grega fi (φ) em homenagem ao escultor Fidias (500-431 a.C.), representa uma relação entre dois segmentos que pertencem à mesma linha.

Esse relacionamento pode não ser apenas verificado em uma abstração geométrica no papel, mas também em flores, folhas e um grande número de formas naturais.

A proporção é muito apreciada pelos artistas plásticos, que o aplicam frequentemente em suas obras e consideram um critério de beleza com validade universal.

O número de proporção de ouro é 1.61803398874989.

Características das proporções

As proporções matemáticas são distinguidas por três características, que são as seguintes:

1- eles são simétricos. Se uma magnitude A é proporcional a outra magnitude B, o último B também é proporcional à magnitude para. Entre eles, há uma relação de simetria ou bidirecional.

2- eles são transitivos. Em uma série proporcional que inclui mais de duas magnitudes, acontece que, se a magnitude A for proporcional ao B, então o B será proporcional a C e o último para D.

3- Eles têm proporcionalidade constante. Esta constante é a razão pela qual três ou mais magnitudes estão em proporção. É obtido como resultado dividindo o antecedente entre o conseqüente de qualquer uma das magnitudes da proporção.

Exemplos de proporções

A escala dos mapas

Certamente você já percebeu que todos os mapas têm, em um canto ou no fundo, alguns números separados por dois pontos (:).

De acordo com o tamanho do mapa, esses números variam entre 1:10.000, 1:50.000, 1: 100.000 ou mesmo 1: 500.000.

Pode atendê-lo: qui-quadrado (χ²): distribuição, como é calculado, exemplos

Esses números indicam a escala do mapa, e uma escala não passa de nada senão uma proporção.

Por exemplo, 1: 100.000 significa que o território representado pelo mapa é, na realidade, 100.000 vezes maior que o mapa que você tem na sua frente. Ou vice -versa: o mapa é 100.000 vezes menores que a área representada.

Folhas de impressão

Quando impressionamos o computador doméstico, aparece uma caixa de diálogo na qual podemos configurar a impressão de acordo com nossas necessidades.

Lá podemos selecionar o tipo de folha em que vamos imprimir, que pode ser A3, A4 ou A5.

Porque acontece que a relação entre os vários formatos da folha é proporcional.

O maior de todos é o A0, que mede um metro quadrado. Segue -se A1, que é metade A0, ou seja, é em proporção de ½.

Então vem A3, que corresponde a ¼ A0 e ½ de A1.

A4 é igual a 1/8 de A0 e ¼ de A1. E finalmente A5, que é 1/16 de A0 e 1/8 de A1.

Referências

1. (S/F). Proporcionalmente constante. Tirado de Edu.Xunta.Garota.
2. (S/F). Propart. Cuemath. Tirado de com.
3. (S/F). Propart. A matemática é divertida. Tirado de Mathsisfun.com.