Pagina inicial
Matemática
Limitar as propriedades (com exemplos)

Matemática

Limitar as propriedades (com exemplos)

4845
1064
Ralph Kohler

As Limitar as propriedades Eles são o conjunto de regras e procedimentos algébricos usados para determinar. O conceito de limite é essencial para o cálculo e a descoberta de que seu valor não precisa ser uma tarefa complicada, desde que suas propriedades sejam tratadas com facilidade.

Abaixo está uma lista dos mais importantes, acompanhados por exemplos de aplicação.

Os limites e suas propriedades são a base do cálculo. Um limite muito especial é mostrado na figura: o derivado de uma função f (x)

Seja B, C, N, A e B números reais e F e g Tais funções que verificam o seguinte:

$\lim_x\rightarrow cf(x)=A$
$\lim_x\rightarrow cg(x)=B$

Então você tem as seguintes propriedades:

1. Limite de substituição direta

Em primeira instância, o limite de uma função f quando x → c pode ser calculado diretamente substituindo x = c na função. Se a função existir em x = c, o limite será:

$\lim_x \rightarrow c f(x)=f(c)$ Mas não necessariamente a função deve ser definida em x = c para que o limite exista. A idéia é abordar tanto quanto você deseja o valor de x = c e ver o que acontece com a função nesse caso.

Exemplo

Encontre o limite de f (x) = x² Quando x → 4

Solução

O limite resolve simplesmente substituindo x = 4 em f (x) = x², Como não há inconveniência na execução da operação:

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Singularidade do limite

Se o limite de uma função f (x) quando x → c existir e vale a pena, o limite é único.

Portanto, os limites laterais, que são aqueles quando x → c^- (Leia “X tende a C da esquerda”) e quando x → C⁺(Ele diz “X tende a C à direita”), ambos existem e têm o mesmo valor L, mesmo que a função não seja definida em x = c.

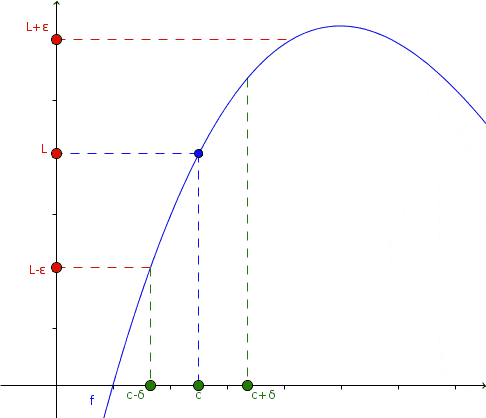Nesta animação, o conceito de limite é apresentado: quando x tende a um certo valor C, aproximando -se da esquerda e da direita, o valor da função tende a l. Não necessariamente a função é definida em x = c. Fonte: Wikimedia Commons.

Na animação, essa abordagem é observada e o que acontece com a função nesse caso: se ela está se aproximando à esquerda e à direita a x = c, o valor da função por sua vez está próximo de L.

Pode atendê -lo: quadrados mínimos

Expressa matematicamente desta maneira:

$\lim_x\rightarrow c^-f(x)=\lim_x\rightarrow c^+f(x)=\lim_x\rightarrow cf(x)=L$ Os limites laterais permitem saber quando existe ou não um limite, porque se eles não existirem ou se diferirem, é certo que o limite da função quando x → c não existe.

Exemplo

Calcule o limite de f (x) quando x → 1 se existir, onde f (x) é dado por:

Solução

Esta é uma função de partes ou definida em pedaços, que consiste na linha 4 -x para os valores de x < 1 y en la parábola 4 - x² Quando x é igual a 1 ou superior a 1.

Podemos abordar x = 1 da esquerda, neste caso a parte da função válida para x é tomada<1:

Como os limites laterais são os mesmos, segue -se que o limite da função quando x → 1 existe e vale 3.

3. Constante

O limite de uma constante é o valor da referida constante, independentemente do valor ao qual a variável tende:

$\lim_x\rightarrow cb=b .$

Exemplo

Calcular:

$\lim_x\rightarrow 1\pi$ Solução

$\lim_x\rightarrow 1\pi= \pi$

4. Limite de função de identidade

Se f (x) = x, sempre é cumprido que:

$\lim_x\rightarrow cx=c$

Exemplo

Calcular:

$\lim_x\rightarrow 2x$ Solução

$\lim_x\rightarrow 2x=2$

5. Limite do produto de uma constante por uma função

Nesse caso, a constante sai do limite e se move para multiplicá -lo, assim:

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Exemplo

Calcule, se existir, o seguinte limite:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Solução

A constante 5 está do lado de fora, multiplicando -se ao limite e a propriedade de substituição é aplicada:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]=5\cdot \lim_x\rightarrow -2 x^3=5\cdot (-2)^3=-40$

6. Limite de soma

O limite da soma de duas funções F e g É a soma dos limites:

$\lim_x\rightarrow c\left [ f(x)+g(x) \right ]=\lim_x\rightarrow c f(x)+\lim_x\rightarrow cg(x)=A+B$

Exemplo

Encontre o seguinte limite se houver:

Pode servir a você: teoria do conjunto: características, elementos, exemplos, exercícios

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Solução

A propriedade da soma dos limites é aplicada primeiro e depois a substituição direta, pois as operações não apresentam dificuldade:

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ] = \lim_\theta \rightarrow \pi cos\: \: \theta + \lim_\theta \rightarrow \pisen\: \: \theta=cos\: \pi +sen\: \pi =-1$

7. Limite de subtração

No caso do limite da subtração de duas funções, proceda de uma maneira análoga que, para a soma: o limite da subtração é a subtração dos limites:

$\lim_x\rightarrow c \left [f(x) - g(x) \right ]=A-B$

Exemplo

Calcule o seguinte limite:

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Solução

A propriedade do limite de subtração de duas funções é aplicada e, em seguida, a substituição direta, pois todas as operações podem ser executadas sem problemas:

$\lim_x \rightarrow 0 [sec\: x - e^x ]=\lim_x \rightarrow 0 sec\: x -\lim_x \rightarrow 0 e^x = sec\: 0-e^0=1-1=0$

8. Limite do produto

O limite do produto de duas funções F e g É o produto dos limites:

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Exemplo

Calcule este limite:

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)$

Solução

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)=\lim_x \rightarrow 0 cos\: x\cdot \lim_x \rightarrow 0 (1-x^2^)=cos\: 0\cdot (1-0^2)=1$

9. Proporção do quociente

O limite da proporção de duas funções F e g É o quociente dos limites, desde que o limite de g (x) quando x → c seja diferente de 0, uma vez que a divisão por 0 não é definida. Então:

$\lim_x \rightarrow c \left [ \fracf(x)g(x) \right ]=\frac\lim_x \rightarrow c f(x)\lim_x \rightarrow c g(x)=\fracAB; \: \: \textupcon\: B\neq 0$

Exemplo

Calcule, se existir, o valor do seguinte limite:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Solução

Em primeira instância, a propriedade Limit da propriedade é aplicada, para obter o quociente dos limites:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]=\frac\lim_x \rightarrow -3 2x-6\lim_x \rightarrow -3 x^2+5$

A propriedade de substituição agora é aplicada para encontrar cada limite:

$\lim_x \rightarrow -3 2x-6=2\cdot (-3)-6=-12$ $\lim_x \rightarrow -3 x^2+5= (-3)^2+5=14$

E desde B ≠ 0, o limite procurado é o quociente A/B:

$\lim_x \rightarrow -3 \frac2x-6x^2+5=\frac-1214=\frac-67$

10. Limite

O limite de um poder de expoente n é equivalente ao limite elevado ao referido poder, como segue:

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Caso 1: Limite de um X Power

Se você tem, por exemplo, o limite de um X Power, resulta:

$\lim_x \rightarrow c x^n=\left [\lim_x \rightarrow c x \right ]^n$

De acordo com a propriedade 4, esse limite é:

Pode atendê -lo: analogias numéricas: tipos, aplicações e exercícios

$\lim_x \rightarrow c x^n=c^n$

Caso 2: limite de raiz

Uma raiz n-Esta pode ser escrita na forma de um expoente fracionário, portanto:

$\lim_x \rightarrow c \sqrt[n]f(x)=\sqrt[n]\lim_x \rightarrow c f(x)$

Importante: Se o índice raiz for par, é necessário que o limite de f (x) quando x → c seja maior ou igual a 0, pois não há pares reais de quantidades negativas.

Exemplos

Determine, aplicando as propriedades anteriores, os seguintes limites se houver:

$a)\: \lim_x \rightarrow -2 (x+5)^^3$

$b)\: \lim_x \rightarrow 3 \sqrt2x-1$

Solução para

Por propriedade do limite de poder e substituição direta, é obtido:

$\lim_x \rightarrow -2 (x+5)^^3= \left [\lim_x \rightarrow -2 (x+5) \right ]^3=(-2+5)^3=27$

Solução b

$\lim_x \rightarrow 3 \sqrt2x-1=\sqrt\lim_x \rightarrow 3 \left (2x-1 \right )=\sqrt(2\cdot 3-1)=\sqrt5$

onze. Limite

Para encontrar o limite de um exponencial B e o expoente F (x), a base da função da função f (x) deve ser levantada da seguinte maneira:

$\lim_x \rightarrow c \left [b^f(x) \right ]=b^\lim_x \rightarrow cf(x)$

Exemplo

Encontre se houver o seguinte limite:

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Solução

Neste limite, a base é o número e e a função f (x) = x², Portanto, você deve primeiro calcular o limite x² Quando x tende a 1:

$\lim_x \rightarrow 1 x^2=1^^2=1$

Em seguida, a propriedade do limite exponencial é aplicada:

$\lim_x \rightarrow 1 e^^x^2=e^^1=e$

12. Limite de função potencial exponencial

O limite quando x → c de uma função f (x), que por sua vez é elevada a outra função g (x) é expressa por:

$\lim_x \rightarrow c \left [f(x)^g(x) \right ]=\left [\lim_x \rightarrow c f(x) \right ]^\lim_x \rightarrow c g(x)$

Exemplo

Calcule o limite a seguir, se existir:

$\lim_x \rightarrow -1 (x-1)^^2x$

Solução

Para aplicar a propriedade anterior, eles são identificados primeiro f (x) = x-1 e g (x) = 2x e, em seguida, os respectivos limites são calculados:

$\lim_x \rightarrow -1 (x-1)=-1-1=-2$

$\lim_x \rightarrow -1 2x=2\cdot (-1)=-2$ Finalmente:

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Referências

Ayres, f. 2000. Cálculo. 5ed. Mc Graw Hill.
Leithold, l. 1992. Cálculo com geometria analítica. Harla, s.PARA.
Textos de matemática gratuitos. Limites. Recuperado de: matemática.Liibretexts.org.
Mathemovil. Leis e limita propriedades. Recuperado de: Matemovil.com.
Larson, r. 2010. Cálculo de uma variável. 9NA. Edição. McGraw Hill.
Purcell, e. J., Varberg, d., & Rigdon, S. E. (2007). Cálculo. México: Pearson Education.
Fórmulas do Universo. Limitar as propriedades. Recuperado de: universoformulas.com

Limitar as propriedades (com exemplos)

1. Limite de substituição direta

Exemplo

Solução

2. Singularidade do limite

Exemplo

Solução

3. Constante

Exemplo

Solução

4. Limite de função de identidade

Exemplo

Solução

5. Limite do produto de uma constante por uma função

Exemplo

Solução

6. Limite de soma

Exemplo

Solução

7. Limite de subtração

Exemplo

Solução

8. Limite do produto

Exemplo

Solução

9. Proporção do quociente

Exemplo

Solução

10. Limite

Caso 1: Limite de um X Power

Caso 2: limite de raiz

Exemplos

Solução para

Solução b

onze. Limite

Exemplo

Solução

12. Limite de função potencial exponencial

Exemplo

Solução

Referências

Melhores artigos

O que é leitura formativa? Tipos e importância

A leitura formativa é um tipo de leitura cujo objetivo é aprender sobre um assunto específico. Promo...

Os 8 tipos de pôsteres de publicidade e suas características

Os tipos de pôsteres de publicidade podem ser divididos de acordo com seu objetivo, conteúdo ou tama...

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Singularidade do limite

$\lim_x\rightarrow 1\pi$ Solução

$\lim_x\rightarrow 2x$ Solução

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Exemplo

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Solução

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Solução

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Solução

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Exemplo

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Solução

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Caso 1: Limite de um X Power

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Solução

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Referências