Propriedade Propriedade Prova, Exemplos

O Propriedade de bloqueio de álgebra É um fenômeno que relaciona dois elementos de um conjunto com uma operação, onde a condição necessária é que, após os 2 elementos sob a referida operação, o resultado também pertence ao conjunto inicial.

Por exemplo, se os números pares são tomados como um todo e uma soma como uma operação, um bloqueio do referido conjunto em relação à soma é obtido. Isso ocorre porque a soma de 2 números pares sempre será dada como resultado, outro número, cumprindo a condição de bloqueio.

Fonte: UNSPASH.com

[TOC]

Caracteristicas

Existem muitas propriedades que determinam espaços ou corpos algébricos, como estruturas ou anéis. No entanto, a propriedade Lock é uma das mais conhecidas na álgebra básica.

Nem todas as aplicações dessas propriedades são baseadas em fenômenos ou elementos numéricos. Muitos exemplos cotidianos podem funcionar de uma abordagem teórica algébrica pura.

Um exemplo pode ser os cidadãos de um país que assumem um relacionamento legal de qualquer tipo, como sociedade comercial ou de casamento entre outros. Após esta operação ou administração, eles ainda são cidadãos do país. Assim, as operações de cidadania e gerenciamento em relação a dois cidadãos representam uma trava.

Álgebra numérica

Com relação aos números, existem muitos aspectos que têm sido um motivo para estudar em diferentes correntes de matemática e álgebra. A partir desses estudos, surgiram um grande número de axiomas e teoremas que servem como base teórica da pesquisa e obras contemporâneas.

Se você trabalha com conjuntos numéricos, podemos estabelecer outra definição válida para a propriedade Lock. Dizem que um conjunto A é a fechadura de outro conjunto B se A é o menor conjunto que contém todos os conjuntos e operações que a casa B.

Pode atendê -lo: propriedade distributiva

Demonstração

A demonstração de bloqueio é aplicada a elementos e operações presentes no conjunto de números N Reais.

Seja A e B dois números que pertencem ao conjunto R, a trava desses elementos é definida para cada operação contida em r.

Adição

- Soma: ∀ a ˄ b ∈ R → a + b = c ∈ R

Esta é a maneira algébrica de dizer que Para todos A e B que pertencem a números reais, deve ser a soma de um mais B é igual a C, que também pertence ao real.

É fácil verificar se essa proposição é verdadeira; É o suficiente para fazer a soma entre qualquer número real e verificar se o resultado também pertence aos números reais.

3 + 2 = 5 ∈ R

-2 + (-7) = -9 ∈ R

-3 + 1/3 = -8/3 ∈ R

5/2 + (-2/3) = 11/6 ∈ R

Observa -se que a condição de bloqueio é atendida para números reais e a soma. Dessa maneira, pode -se concluir: A soma dos números reais é uma trava algébrica.

Multiplicação

- Multiplicação: ∀ a ˄ b ∈ R → A . B = c ∈ R

Para todos A e B que pertencem aos reais, a multiplicação de A para B é igual a C, que também pertence ao real.

Ao verificar com os mesmos elementos do exemplo anterior, os seguintes resultados são observados.

3 x 2 = 6 ∈ R

-2 x (-7) = 14 ∈ R

-3 x 1/3 = -1 ∈ R

5/2 x (-2/3) = -5/3 ∈ R

Esta é uma evidência suficiente para concluir que: A multiplicação de números reais é uma trava algébrica.

Esta definição pode ser estendida a todas as operações de números reais, embora encontremos certas exceções.

Fonte: Pixabay.com

Casos especiais em r

Divisão

Como um caso especial, a divisão é observada, onde a seguinte exceção é apreciada:

Pode servir a você: probabilidade clássica: cálculo, exemplos, exercícios resolvidos

∀ a ˄ b ∈ R → a / b ∉ r ↔ b = 0

Para todos A e B que pertencem a R É necessário entre B não pertence ao reais se e somente se B for igual a zero.

Este caso refere -se à restrição de não ser capaz de dividir entre zero. Como zero pertence aos números reais, conclui -se que: euDivisão não é um bloqueio no real.

Rádio

Também existem operações de potenciação, mais especificamente as do arquivamento, onde as exceções são apresentadas para o índice de torque dos poderes radicais:

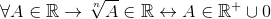; Com n par

Para tudo ao qual pertence ao real.

Dessa maneira, é indicado que as raízes uniformes se aplicam apenas às reais positivas e conclui -se que a potencialização não é uma trava em r.

Logaritmo

É aprovado para a função logarítmica, que não é definida para valores menores ou iguais a zero. Para verificar se o logaritmo é um rock r ruck da seguinte forma:

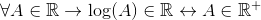
Para tudo o que pertence aos reais, o logaritmo de A pertence aos reais, se e somente se pertencer ao real positivo.

Quando os valores negativos e zero que também pertencem a r são excluídos, pode -se afirmar que:

O logaritmo não é um bloqueio de números reais.

Exemplos

Verifique o bloqueio para obter a soma e a subtração de números naturais:

Soma em n

A primeira coisa é verificar a condição de bloqueio para diferentes elementos do conjunto fornecido, onde se for observado que algum elemento quebra com a condição, a existência de bloqueio pode ser negado automaticamente.

Pode servir a você: Rádio de Convergência: Definição, Exemplos e Exercícios resolvidos

Esta propriedade é atendida para todos os valores possíveis de A e B, conforme observado nas seguintes operações:

1 + 3 = 4 ∈ N

5 + 7 = 12 ∈ N

1000 + 10000 = 11000 ∈ N

Não há valores naturais que quebrem a condição de bloqueio, por isso está concluído:

A soma é uma trava em n.

Subtrai em n

Os elementos naturais são procurados capazes de quebrar a condição; A - B pertence aos nativos.

Operando, é fácil encontrar pares de elementos naturais que não atendem à condição de bloqueio. Como por exemplo:

7 - 10 = -3 ∉ a n

Dessa forma, podemos concluir que:

A subtração não é uma fechadura do conjunto de números naturais.

Exercícios propostos

1 samp.

2-explicar se o conjunto de números reais for um bloqueio de todo o número inteiro.

3 determinantes que conjunto numérico pode ser o bloqueio de números reais.

4-amostra a propriedade de bloqueio para o conjunto de números imaginários, com relação à soma, subtração, multiplicação e divisão.

Referências

1. Panorama de matemática pura: a escolha do Bourbakist. Jean Dieudonné. Reverte, 1987.
2. Teoria dos números algébricos. Alejandro J. Díaz Barriga, Ana Irene Ramírez, Francisco Tomás. Universidade Autônoma Nacional do México, 1975.
3. Álgebra linear e suas aplicações. Sandra Ibeth Ochoa García, Eduardo Gutiérrez González.
4. Estruturas algébricas V: teoria do corpo. Héctor a. Merklen. Organização dos Estados Americanos, Secretaria Geral, 1979.
5. Introdução à álgebra comutativa. Michael Francis Atiyah, eu. G. MacDonald. Reverte, 1973.