Características do processo político, aplicações e exemplos

A Processo político É um processo termodinâmico que ocorre quando a relação entre pressão P e o volume V dado por P.Vⁿ Permanece constante. O expoente n É um número real, geralmente entre zero e infinito, mas em alguns casos pode ser negativo.

O valor de n receber o nome de Índice de Politropy E é importante destacar que durante um processo termodinâmico politrópico disse que o índice deve manter um valor fixo, caso contrário, o processo não será considerado politrópico.

figura 1. Equação característica de um processo termodinâmico politrópico. Fonte: f. Zapata.

[TOC]

Características de processos politrópicos

Alguns casos característicos de processos politrópicos são: 

- O processo isotérmico (em temperatura constante), na qual o expoente é n = 1.

- Um processo isobárico (pressão constante p), neste caso n = 0.

- O processo isocórico (para o volume V constante), para o qual n =+∞.

- Processos adiabáticos (para entropia constante), na qual o expoente é n = γ, sendo γ a constante adiabática. Esta constante é o quociente entre a capacidade de calor a pressão constante, dividida pela capacidade de calor no volume constante de CV:

γ = CP/CV

- Qualquer outro processo termodinâmico que não seja nenhum dos casos anteriores. Mas cumpra P.Vⁿ = ctte Com índice politrópico real e constante n Também será um processo politrópico.

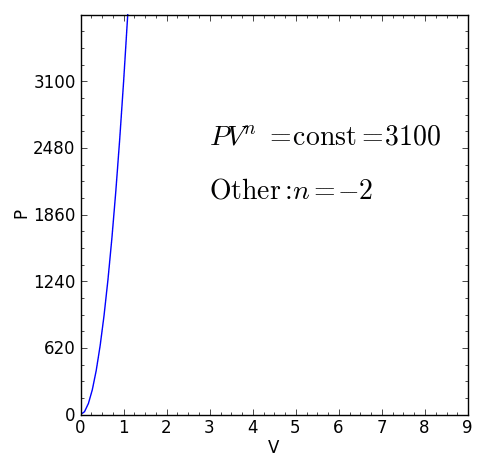Figura 2. Diferentes casos característicos de processos termodinâmicos politrópicos. Fonte: Wikimedia Commons.

Formulários

Uma das principais aplicações da equação politrópica é o cálculo do trabalho realizado por um sistema termodinâmico fechado, quando passa de um estado inicial para outra extremidade de maneira quase estática, ou seja, seguindo uma sucessão de estados de equilíbrio.

Trabalhe em processos politrópicos para diferentes valores de n

Para n ≠ 1

O trabalho mecânico realizado por um sistema termodinâmico fechado é calculado por expressão:

W = ∫P.Dv

Pode servir a você: diamagnetismo: materiais, aplicações, exemplos

Onde p é a pressão e v o volume.

Como no caso de um processo politrópico, a relação entre pressão e volume é:

P.V ⁿ = constante = c

Limpando P da expressão anterior para substituí -la na expressão do trabalho:

P = c /V ⁿ

Você tem o trabalho mecânico realizado durante um processo politrópico, que começa em um estado inicial 1 e termina no estado final 2. Tudo isso aparece na seguinte expressão:

Se n ≠ 1, então você tem:

Além disso, como os estados iniciais e finais são bem definidos, a constante também é determinada pela seguinte expressão:

C = p₁ V₁ⁿ = P₂ V₂ⁿ

Ao substituir o valor da constante na expressão do trabalho, é obtido:

W = (P₂ V₂ - P₁ V₁)/(1-n)

No caso de a substância de trabalho ser modelada como um gás ideal, a seguinte equação de estado é:

P.V = m.R.T

Onde m é o número de moles de gás ideal e r é a constante universal de gases.

Para um gás ideal que segue um processo politrópico com um índice de poltropia diferente da unidade e que passa de um estado com temperatura inicial t₁ para outro estado com temperatura t₂ O trabalho realizado é dado pela seguinte fórmula:

W = m r (t₂ - T₁)/(1-n)

Para n → ∞

De acordo com a fórmula para o trabalho obtido na seção anterior, o trabalho de um processo politrópico com n = ∞ é nulo, porque a expressão do trabalho é dividida entre o infinito e, portanto, o resultado tende a zero.

Outra maneira de alcançar esse resultado é começar a partir do relacionamento P₁ V₁ⁿ = P₂ V₂ⁿ, que pode ser reescrito da seguinte maneira:

(P₁/P₂) = (V₂/V1)ⁿ

Tomando a raiz n-thicker em cada membro que você recebe:

(V₂/V1) = (P₁/P₂)^(1/n)

No caso que n → ∞, você precisa (v₂/V1) = 1, o que significa que:

Pode servir você: calor cedido: fórmulas, como calculá -lo e exercícios resolvidos

V₂ = V₁

Isto é, o volume não muda em um processo politrópico com n → ∞. Portanto, o diferencial de volume de DV na integral do trabalho mecânico é 0. Esses tipos de processos politrópicos também são conhecidos como processos isocórico, o Processos em volume constante.

Para n = 1

Novamente, temos a expressão para o trabalho:

W = ∫P DV

No caso de um processo politrópico com n = 1, a relação entre pressão e volume é:

P v = constante = c

Ao limpar P da expressão anterior e substituindo, você tem o trabalho realizado para ir do estado inicial 1 para o estado final 2:

W = ∫12p dv = ctte ∫12 v^( - 1) dv = ctte (ln (v2) - ln (v1))

Quer dizer:

W = C ln (V₂/V₁).

Como os estados iniciais e finais estão bem determinados, o mesmo acontece com o CTTE. Quer dizer:

C = p₁ V₁ = P₂ V₂

Finalmente, as seguintes expressões úteis estão disponíveis para encontrar o trabalho mecânico de um sistema fechado politrópico no qual n = 1.

W = p₁ V₁ ln (v₂/V₁) = P₂ V₂ ln (v₂/V₁)

Se a substância de trabalho consistir em m Moles de gás ideal, então a equação ideal do gás pode ser aplicada: p v = m.R.T.

Nesse caso, como P.V₁ = CTTE, um processo politrópico com n = 1 é um processo à temperatura constante t (isotérmica), para que as seguintes expressões para o trabalho possam ser obtidas:

W = m r t₁ ln (v₂/V₁) = m r t₂ ln (v₂/V₁)

Figura 3. Um derretimento de caramban, exemplo de processo isotérmico. Fonte: Pixabay.

Exemplos de processos politrópicos

- Exemplo 1

Suponha um cilindro com um pistão móvel cheio com um quilograma de ar. Inicialmente o ar ocupa um volume V₁= 0,2 m³ a uma pressão p₁= 400 kPa. Um processo politrópico é seguido com n = γ = 1,4, cujo estado final tem pressão p₂ = 100 kPa. Determine o trabalho realizado pelo ar no pistão.

Solução

Quando o índice de poltropia é igual à constante adiabática, há um processo no qual a substância de trabalho (ar) não troca calor com o ambiente e, portanto, não muda de entropia.

Pode servir a você: Terceira Lei da Termodinâmica: Fórmulas, Equações, Exemplos

Para o ar, um gás diatômico ideal, você tem:

γ = cp/cv, com cp = (7/2) r e cv = (5/2) r

Então:

γ = 7/5 = 1,4

Usando a expressão do processo politrópico, o volume final do ar pode ser determinado:

V₂ = [P₂ V₁^1.4)/P₂]^(1/1.4) = 0,54 m³.

Agora, existem condições para aplicar a fórmula de trabalho feita em um processo politrópico para n ≠ 1 obtido acima:

W = (P₂ V₂ - P1 v1)/(1-n)

Substituindo os valores apropriados são:

W = (100 kPa 0,54 m³ - 400 kpa 0,2 m³)/(1 - 1.4) = 65,4 kJ

- Exemplo 2

Suponha o mesmo cilindro do Exemplo 1, com um pistão móvel cheio com um quilograma de ar. Inicialmente o ar ocupa um volume V1 = 0,2 m³ a uma pressão p1 = 400 kPa. Mas, diferentemente do caso anterior, o ar expande isotermicamente para atingir uma pressão final P2 = 100 kPa. Determine o trabalho realizado pelo ar no pistão.

Solução

Como visto anteriormente, os processos isotérmicos são processos politrópicos com índice n = 1, por isso é cumprido que:

P1 v1 = p2 v2

Dessa maneira, o volume final pode ser facilmente desapegado para obter:

V2 = 0,8 m³

Em seguida, usando a expressão do trabalho anteriormente obtido para o caso n = 1, você deve trabalhar pelo ar no pistão nesse processo é:

W = P1 V1 LN (V2/V1) = 400000 PA × 0,2 m³ LN (0,8/0,2) = 110,9 kJ.  

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill.
2. Cengel, e. 2012. Termodinâmica. 7ª edição. McGraw Hill.
3. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 4. Fluidos e termodinâmica. Editado por Douglas Figueroa (USB).
4. López, c. A primeira lei da termodinâmica. Recuperado de: culturacientifica.com.
5. Cavaleiro, r. 2017. Física para cientistas e engenharia: uma abordagem de estratégia. Pearson.
6. Serway, r., Vulle, c. 2011. Fundamentos da Física. 9na ed. Cengage Learning.
7. Universidade Sevilla. Máquinas térmicas. Recuperado de: Laplace.nós.é.
8. Wikiwand. Processo político. Recuperado de: wikiwand.com.