Tipos de processo adiabático, exemplos, exercícios resolvidos

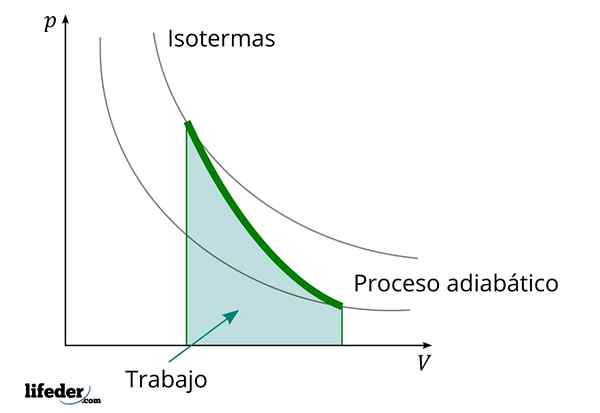
A Processo adiabático É aquele em que não há troca de calor entre o sistema e seus arredores, porque ocorre dentro de um meio isolante ou porque passa muito rapidamente. Isso significa que, nos arredores do sistema, isto é, a parte do universo em estudo, as mudanças de temperatura não devem ser percebidas, mas apenas funcionam.

Este é um dos processos elementares da termodinâmica. Ao contrário dos outros processos (isocóricos, isobáticos e isotérmicos), nenhuma de suas variáveis ​​físicas permanece constante; isto é, as magnitudes de pressão, volume, temperatura e entropia mudam à medida que o processo adiabático evolui.

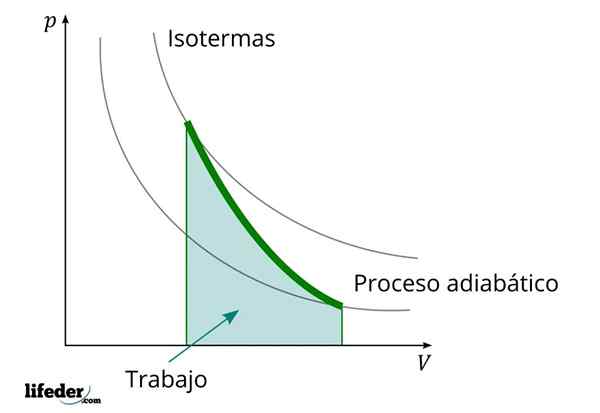Durante um processo adiabático no qual o volume aumenta, a energia interna da substância que o trabalho diminui

Outra característica importante dos processos adiabáticos é que eles realizam ou consomem trabalho proporcionalmente à variação da energia interna de seus sistemas; Nesse caso, dos de suas moléculas em uma fase gasosa. Isso pode ser demonstrado graças à primeira lei da termodinâmica.

Na vida cotidiana, esse tipo de processo abrange acima de tudo para fenômenos geofísicos e, até certo ponto, o funcionamento dos pistões nos motores a diesel. A transferência de calor é frequentemente evitada com o uso de um meio isolante, mas é a velocidade desses processos que permite seu desenvolvimento real.

[TOC]

Processos adiabáticos reversíveis e irreversíveis

Reversível

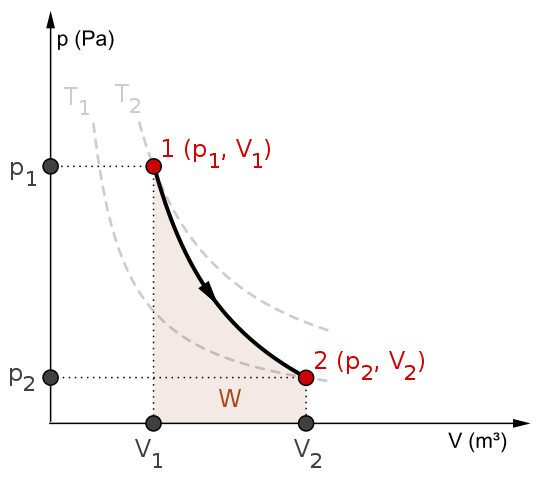Diagrama de P-V e trabalho W para um processo adiabático. Fonte: Mikerun/CC BY-SA (https: // CreativeCommons.Org/licenças/BY-SA/4.0)

Processos adiabáticos podem ser reversíveis ou irreversíveis. No entanto, o primeiro existe apenas como ferramentas teóricas para estudar o último. Assim, os processos adiabáticos reversíveis envolvem os gases ideais e não têm atrito e qualquer outra eventualidade que cause uma transferência de calor entre o sistema e seus arredores.

Considere, por exemplo, o diagrama P-V para o processo adiabático reversível de cima. T₁ e T₂ corresponde a duas isotermas, nas quais as pressões P e os volumes V do sistema varia.

Entre os estados (P₁, V₁) E P₂, V₂) É realizada uma expansão adiabática reversível, pois passamos de um volume V₁ para um v₂, maior, seguindo a direção da flecha.

Ao fazer isso, o sistema esfria, mas sem obedecer ao comportamento das isotermas. A área sob a curva corresponde ao trabalho w, cujo valor é positivo porque é uma expansão.

Nesse processo, a entropia permanece constante e, portanto, diz -se que é isontrópico. O processamento matemático dessa reversibilidade gera um conjunto de equações com as quais é possível avaliar outros sistemas.

Pode atendê -lo: células eletrolíticas

Irreversível

Processos adiabáticos irreversíveis, diferentemente dos reversíveis, não são gráficos nos diagramas P-V com linhas contínuas, mas pontilhadas, uma vez que apenas os estados finais e iniciais têm suas variáveis ​​(P, V e T) bem definidas. Esses processos envolvem gases reais; portanto, a equação de gases ideais e suas derivações não são diretamente aplicáveis ​​a eles.

Eles passam rapidamente, impedindo a transferência de calor entre o sistema e seus arredores. Além disso, neles a entropia aumenta, conforme declarado na Segunda Lei da Termodinâmica.

Exemplos de processos adiabáticos

A capacidade de isolamento, como a apresentada pela ThermoM, é um dos principais fatores para um processo para desenvolver adiabaticamente

Alguns exemplos de processos adiabáticos serão mencionados abaixo.

Expansão e compreensão

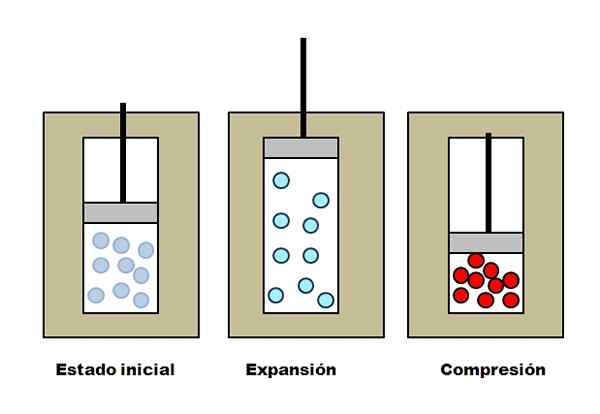Expansão e compreensão adiabática. Fonte: Gabriel Bolívar.

Suponha que três coletes isolantes contendo compartimentos cheios de gás. Em um estado inicial, o pistão não tem pressão sobre o gás. Em seguida, o pistão pode aumentar, o que aumenta o volume através do qual as moléculas de gás podem se mover, causando uma diminuição em sua energia interna; E, portanto, uma diminuição na temperatura.

O oposto acontece com a compressão adiabática: o pistão realiza trabalho sobre gás, reduzindo o volume que suas moléculas podem ocupar. A energia interna aumenta esse tempo, o que também implica um aumento de temperatura, cujo calor não pode se dispersar em direção ao ambiente por causa do colete isolante.

Magma Ascent

Os canais onde o magma sobe dentro de um vulcão dizem como um meio isolante, o que impede a transferência de calor entre magma e atmosfera.

Som espalhado

Os gases são perturbados e expandidos de acordo com a onda sonora sem resfriar ou quente o ar que os rodeia.

Efeito Foehn

O efeito Foehn é um exemplo de processos adiabáticos no campo da geofísica. As massas de ar ascendem em direção à parte superior de uma montanha, onde experimentam menos pressão, de modo que suas moléculas se expandem e esfriam, dando origem à formação da nuvem.

No entanto, eles mal descem do outro lado da montanha, a pressão aumenta e, portanto, as moléculas são comprimidas e aumentam sua temperatura, fazendo com que a nuvem desapareça.

Pode atendê -lo: clorobenzeno (C6H5Cl)

No vídeo seguinte, esse fenômeno pode ser apreciado:

Exercícios resolvidos

Finalmente, alguns exercícios serão resolvidos. É importante ter as seguintes equações em questão:

ΔU = Q - W (Primeira Lei da Termodinâmica)

Mas não transferindo o calor, q = 0 y:

ΔU = - W (1)

Isto é: se o trabalho w é positivo, Δu é negativo e vice -versa. Por outro lado, também temos:

W = -nC_VΔt (2)

Que depois de aplicar a equação GASE ideal (PV = nRt), e substituindo e resolvendo T para T₂ e T₁ nós teremos:

W = (C_V/R) (P₁V₁ - P₂V₂) (3)

Sendo o valor de R igual a 0.082 L · atm/mol · k ou 8.314 J/mol · k

Nos processos adiabáticos, é importante conhecer o relacionamento C_P/C_V conhecido como γ:

γ = c_P/C_V    (4)

Que permite estabelecer relações T-V e P-V:

T₁V₁^γ-1 = T₂V₂^γ-1   (5)

P₁V₁^γ = P₂V₂^γ    (6)

E também, os calorosos aproximados de C_P e C_V Eles variam dependendo se os gases são monoatômicos, diatômicos, etc.

Exercício 1

Um gás realiza 600 j de trabalho através de um compartimento isolado. Qual é a mudança em sua energia interna? A temperatura diminui ou aumenta? E considerando que é um gás monoatômico, também calcule γ.

Dados:

W = +600J

ΔU = ¿?

γ =?

W O trabalho é positivo porque o gás funciona nos arredores. Estar dentro de um compartimento isolado, q = 0, e, portanto, teremos a Equação (1):

ΔU = - W

Isto é, Δu é igual a:

ΔU = - (+600J)

= -600J

O que significa que a energia interna do gás diminuiu 600 J. Se ΔU diminuir, o mesmo ocorre com a temperatura, o gás esfria como resultado de ter feito o trabalho.

Porque esse gás é monoatômico,

C_V = 3/2 r

C_P = 5/2 r

E sendo

γ = c_P/C_V

= (5/2 r)/(3/2 r)

= 5/3 ou 1.66

Exercício 2

Em um recipiente 7 moles de O₂ Eles foram compactados de um volume de 15 litros a 9 litros. Sabendo que a temperatura inicial era de 300 K, calcule: o trabalho realizado no gás.

Dados:

n = 7 moles ou₂

T₁ = 300 k

V₁ = 15 l

V₂ = 9 l

W = ¿?

É um entendimento adiabático irreversível. Temos duas equações para resolver w:

W = -nC_VΔt (2)

W = (C_V/R) (P₁V₁ - P₂V₂) (3)

As pressões podem calculá -las, mas para economizar tempo, é melhor prosseguir com a primeira das equações:

Pode atendê -lo: água destilada

W = -nC_VΔt

= -nC_V (T₂-T₁)

Precisamos de c_V e T₂ Para determinar w. Oxigênio, sendo um gás diatômico, tem um c_V igual a 5/2 r:

C_V (QUALQUER₂) = 5/2 r

= 5/2 (8.314 J/mol · k)

= 20.785 J/mol · k

Precisamos calcular T₂. Voltamos à Equação (5):

T₁V₁^γ-1 = T₂V₂^γ-1

Mas antes de usá -lo, você deve determinar o primeiro C_P e γ:

C_P (QUALQUER₂) = 7/2 r

= 7/2 (8.314 J/mol · k)

= 29.099 J/mol · k

Sendo γ igual a:

γ = c_P/C_V

= (29.099 J / mol · k) / 20.785 J/mol · k

= 1.4

Então, podemos limpar isso₂ Da Equação (5):

T₁V₁^γ-1 = T₂V₂^γ-1

T₂ = (T₁V₁^γ-1) / (V₂^γ-1)

= [(300K) (15L)^1.4-1] / (9L)^1.4-1

= 368.01 k

E finalmente resolvemos W:

W = -nC_VΔt

= -(7 mol o₂)( vinte.785 J/mol · k) (368.01 K - 300 K)

= -9895.11 J O -9.895 KJ

Exercício 3

Um recipiente de neon se expande adiabático e inicialmente à temperatura ambiente (t = 298k) de 12 L para 14 L. Sabendo que sua pressão inicial era de 3 atm, qual será o trabalho realizado pelo gás?

Dados:

T₁ = 298 k

V₁ = 12 l

V₂ = 14 l

P₁ = 3 atm

W = ¿?

A equação (3) nos permite determinar w com os valores das pressões:

W = (C_V/R) (P₁V₁ - P₂V₂)

Mas estamos perdendo C_V E P₂.

A pressão final pode ser calculada com a equação (6):

P₁V₁^γ = P₂V₂^γ

Sendo γ igual a C_P/C_V. Como o neon é um gás monoatômico, temos seus valores C_P e C_V Eles são 5/2r e 3/2r, respectivamente. Calculamos então γ:

γ = c_P/C_V

= (5/2r)/(3/2r)

= 5/3 ou 1.66

Limparemos p₂ Da Equação (6):

P₂ = (P₁V₁^γ) / V₂^γ

= [(3 atm) (12 L)^5/3] / (14 L)^5/3

= 1.40 atm

E o trabalho será igual a:

W = (C_V/R) (P₁V₁ - P₂V₂)

= (3/2) [(3 atm) (12 L) - (1.40 atm) (14 L)] (101300 pa/1 atm) (0.001 m³/L) (KJ/1000 J)

= 2.49 KJ

Fatores de conversão são usados ​​para converter o l · atm a pa · m³, que é equivalente a 1 j. O gás neon se expande, então sua pressão diminui e, ao trabalhar no ambiente, isso é positivo. Além disso, sua energia interna ΔU diminui, bem como sua temperatura, resfriamento no processo de expansão.

Referências

1. Walter J. Moore. (1963). Química Física. Em cinética química. Quarta edição, Longmans.
2. Irã. Levine. (2009). Princípios da físico -química. Sexta edição. Mc Graw Hill.
3. Wikipedia. (2020). Processo adiabático. Recuperado de: em.Wikipedia.org
4. Jones, Andrew Zimmerman. (18 de agosto de 2020). Themodinâmica: Processo Adiabático. Recuperado de: pensamento.com
5. Devoe Howard e Neils Tom. (9 de agosto de 2020). Alterações adiabáticas. Química Librettexts. Recuperado de: química.Librettexts.org