Conceito de probabilidade de frequência, como é calculado e exemplos

O A probabilidade de frequência é uma sub-definição no estudo da probabilidade e seus fenômenos. Seu método de estudo em relação a eventos e atributos é baseado em grandes quantidades de iterações, observando, cada uma a longo prazo ou mesmo infinitas repetições.

Por exemplo, um envelope Gummitan contém 5 borrachas de cada cor: azul, vermelho, verde e amarelo. Você deseja determinar a probabilidade de que cada cor tenha que sair após uma seleção aleatória.

Fonte: pexels

É tedioso imaginar pegar uma borracha, gravar, devolvê -lo, retirar uma borracha e repetir as mesmas centenas ou milhares de vezes. Você pode até querer observar o comportamento após vários milhões de iterações.

Mas, pelo contrário, é interessante descobrir que, após poucas repetições, a probabilidade esperada de 25% não é totalmente cumprida, pelo menos não para todas as cores após 100 iterações ocorrem.

Sob a abordagem de probabilidade de frequência, a alocação de valores será somente através do estudo de muitas iterações. Dessa maneira, o processo deve ser realizado e de preferência registrado de maneira computadorizada ou emulada.

Várias correntes rejeitam a probabilidade de frequência, argumentando a falta de empirismo e confiabilidade em critérios aleatórios.

[TOC]

Como é calculada a probabilidade de frequência?

Ao programar o experimento em qualquer interface capaz de oferecer uma iteração puramente aleatória, você pode começar a estudar a probabilidade de frequência do fenômeno através de uma tabela de valores.

O exemplo anterior é apreciado pela abordagem de frequência:

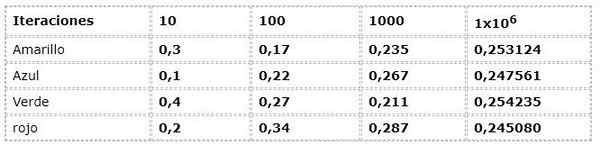
Dados numéricos correspondem à expressão:

N (a) = número de ocorrências/ número de iterações

Onde n (a) representa a frequência relativa do evento "a"

“A” pertence ao conjunto de resultados possíveis ou espaço de amostra ω

Pode atendê -lo: múltiplos de 8: o que são e explicação

Ω: vermelho, verde, azul, amarelo

Existe uma dispersão considerável nas primeiras iterações, quando frequências com até 30% das diferenças são observadas entre si, o que é um fato muito alto para um experimento que teoricamente tem eventos com a mesma possibilidade (equipamento).

Mas à medida que as iterações crescem, os valores parecem cada vez mais aos apresentados pela corrente teórica e lógica.

Lei dos grandes números

Como um acordo inesperado entre as abordagens teóricas e de frequência, surge a lei de grandes números. Onde está estabelecido que, após uma quantidade considerável de iterações, os valores do experimento de frequência estão se aproximando de valores teóricos.

No exemplo, você pode notar como os valores são aproximados de 0,250 à medida que as iterações crescem. Este fenômeno é elementar nas conclusões de muitas obras probabilísticas.

Fonte: pexels

Outras abordagens de probabilidade

Existem outras 2 teorias ou abordagens para a noção de probabilidade, além do Probabilidade de frequência.

Teoria lógica

Sua abordagem é orientada para a lógica dedutiva dos fenômenos. No exemplo anterior, a probabilidade de obter cada cor é 25% fechada. Em outras palavras.

Teoria subjetiva

É baseado no conhecimento e nas crenças anteriores que cada indivíduo tem sobre os fenômenos e atributos. Declarações como "Sempre chove na semana santa " Eles obedecem a um padrão de eventos semelhantes que ocorreram anteriormente.

História

O início de sua data de implementação do século XIX, quando a cito em vários de seus trabalhos em Cambridge England. Mas não foi até o século XX que 2 Matemática Estatística desenvolveu e moldou o Probabilidade de frequência.

Pode atendê -lo: equações polinomiais

Um deles foi Hans Reichenbach, que desenvolve seu trabalho em publicações como "Teoria da Probabilidade" publicada em 1949.

O outro foi Richard von Mises, que desenvolveu seu trabalho mais minuciosamente através de várias publicações e propôs considerar a probabilidade como uma ciência matemática. Esse conceito era novo em matemática e marcaria o início de uma era de crescimento no estudo do Probabilidade de frequência.

Na verdade, este evento faz a única diferença com as contribuições feitas pela geração de Venn, Coulot and Helm. Onde a probabilidade se torna uma contraparte, como geometria e mecânica.

< La teoría de las probabilidades trata con fenômenos maciços e eventos repetitivos. Problemas nos quais o mesmo evento é repetido repetidamente, ou um grande número de elementos uniformes está envolvido ao mesmo tempo>> Richard von Mises

Fenômenos maciços e eventos repetitivos

Três tipos podem ser classificados:

• Física: Obdose Padrões da natureza além de uma condição aleatória. Por exemplo, o comportamento das moléculas de um elemento em uma amostra.
• Chance: sua consideração fundamental é a aleatoriedade, pois liberando um dado repetidamente.
• Estatística biológica: seleções de sujeitos de teste de acordo com suas características e atributos.

Na teoria, o indivíduo que mede desempenha um papel nos dados probabilísticos, porque é o seu conhecimento e experiências que articulam esse valor ou previsão.

No Probabilidade de frequência Os eventos serão considerados como coleções a serem tratados, onde o indivíduo não desempenha nenhum papel na estimativa.

Atributos

Em cada elemento, ocorre um atributo, que será variável de acordo com a natureza deste. Por exemplo, no tipo de fenômeno físico, as moléculas de água terão velocidades diferentes.

Pode atendê -lo: critérios de similaridade triangulosa

No lançamento dos dados, conhecemos o espaço de amostra ω que representa os atributos do experimento.

Ω: 1, 2, 3, 4, 5, 6

Existem outros atributos, como ω_P  ou seja ω ω_Yo

Ω_p : 2, 4, 6

Ω_Yo : 1, 3, 5

Que pode ser definido como atributos não elementares.

Exemplo

• Você deseja calcular a frequência de cada soma possível no lançamento de dois dados.

Para isso, um experimento é programado onde dois valores aleatórios entre [1, 6] são adicionados em cada iteração.

Os dados são registrados em uma tabela e as tendências em grande número são estudadas.

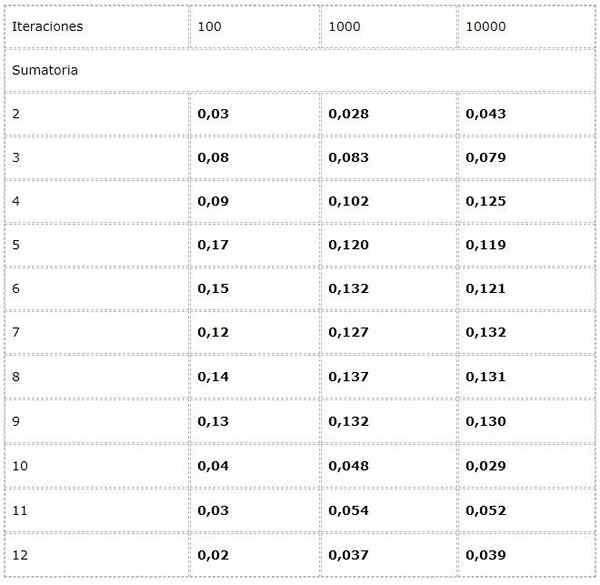
Observa -se que os resultados podem variar significativamente entre as iterações. No entanto, a lei de grandes números pode ser vista na aparente convergência apresentada nas duas últimas colunas.

Referências

1. Estatísticas e avaliação de evidências para cientistas forenses. Segunda edição. COLIN G.G. Aitken. Escola de Matemática. Universidade de Edimburgo, Reino Unido
2. Matemática para Ciência da Computação. Eric Lehman. Google Inc.
   F Thomson Leighton Departamento de Matemática e Laboratório de Ciência da Computação e AI, Instituto de Tecnologia de Massachussetts; Akamai Technologies
3. O professor aritmético, volume 29. Conselho Nacional de Professores de Matemática, 1981. Universidade de Michigan.
4. Teoria dos números de aprendizado e ensino: pesquisa em cognição e instrução / editado por Stephen R. Campbell e Rina Zazkis. Publicação Ablex 88 Post Road West, Westport CT 06881
5. Bernoulli, J. (1987). ARS conjetandi- 4ème partie. ROUEN: IREM.