Prisma hexagonal

Explicamos o que é um prisma hexagonal, suas características, elementos, área, vértices, bordas e como calculá -los.

O que é um prisma hexagonal?

A Prisma hexagonal É um corpo tridimensional composto por duas formas de hexágono e lados em forma de retângulo ou paralelograma. Pode ser encontrado na natureza, na estrutura cristalina de minerais como berílio, grafite, zinco e lítio, por exemplo.

Os elementos de um prisma hexagonal são a base, o rosto, borda, altura, vértice, rádio e apothem. A partir deles, você pode calcular áreas e volumes.

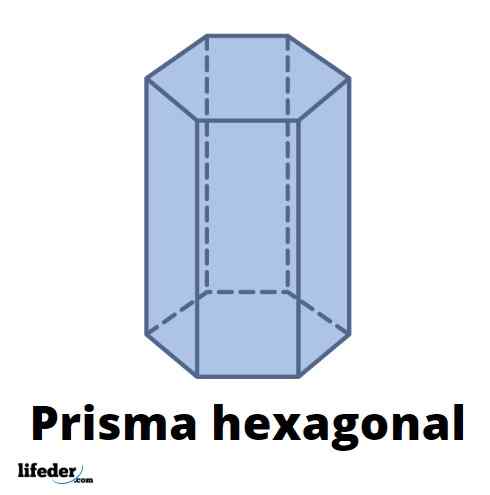
A figura superior mostra um prisma hexagonal com faces laterais retangulares; quer dizer, Um prisma hexagonal direto. Os hexágonos das bases são regulares, ou seja, seus lados internos e ângulos são os mesmos. No entanto, os rostos hexagonais de prisma podem ser hexágonos irregulares.

Características do prisma hexagonal

1- Prisma hexagonal é uma figura tridimensional com bases hexagonais.

2- Há uma grande variedade de objetos que respondem a essa definição e, no entanto, eles são bem diferentes.

Na figura seguinte, há uma variedade de prismas hexagonais: à esquerda, um prisma hexagonal reto de rostos regulares, à direita e abaixo de dois prismas hexagonais de rostos irregulares. O hexágono na base do prisma abaixo tem uma particularidade: é côncavo, O que significa que alguns de seus ângulos internos são maiores que 180 °.

Variedade de prismas hexagonais. Fonte: Wikimedia Commons.

Por outro lado, as bases hexagonais dos prismas acima são polígonos convexo: Todos os ângulos internos medem menos de 180 °.

Elementos de prisma hexagonal

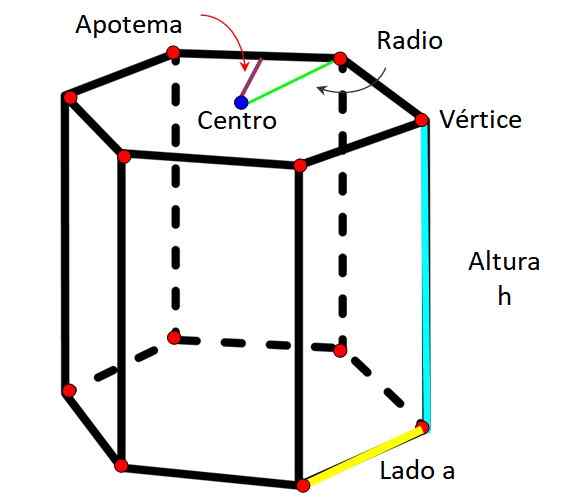Elementos de prisma hexagonal. Fonte: f. Zapata

Como todo prisma, o prisma hexagonal é caracterizado por ter os seguintes elementos:

Pode servir a você: inverso multiplicativo: explicação, exemplos, exercícios resolvidos

-Bases: em número de dois (2), na forma de hexagon e congruente, isto é, de igual medida. Os rostos hexagonais podem ser regulares ou irregulares.

-Rostos: Um prisma hexagonal tem oito (8) rostos no total, que podem ser contados usando a Figura 1. Das 8 faces, duas (2) são bases e seis (6) são laterais.

-Borda: É o segmento que se junta a duas bases ou dois lados do prisma.

-Altura: É a distância entre as duas faces do prisma. Coincide com o comprimento da borda em caso de prisma direta.

-Vértice: ponto comum entre uma base e dois lados lados.

Se as bases do prisma são regulares, a simetria da figura permite definir elementos adicionais do lado hexágono comum para.

-Rádio: É a distância medida do centro do hexágono e de qualquer vértice.

-Apótema: É o segmento que vai do centro do rosto hexagonal para o meio de um lado.

Com a ajuda desses elementos, áreas e volumes são calculados, como veremos mais adiante.

Fórmulas

Existem inúmeras fórmulas relacionadas ao prisma hexagonal. Eles servem para calcular a área de suas bases e rostos laterais, seu volume e outras características importantes. As áreas de hexágono regular, hexágono irregular e paralelograma, bem como os perímetros, são úteis.

Perímetro de uma figura plana

É a medida de seu contorno, que no caso de um polígono como o hexagon é a soma de seus lados. Se o hexágono estiver regularmente de lado para, Há uma fórmula para o perímetro P:

P = 6.para

Área hexágona regular

Vamos chamar ALS e L_PARA Na duração do apoteme. A área é dada por:

Pode atendê -lo: dados não agrupados: exemplos e exercícios resolvidos

A = p. eu_PARA/2 = 6a. eu_PARA/2

Onde P é o perímetro da figura.

Dependendo do tamanho do lado para, A área também pode ser calculada por:

A = 2.5981.para²

Área de hexagon irregular

Não existe uma fórmula específica, pois depende do arranjo dos lados, mas o hexágono pode ser dividido em triângulos, calcule a área de cada um e adicione -os.

Outro método para encontrar a área é o dos determinantes de Gauss, para os quais é necessário conhecer as coordenadas dos vértices hexágonos.

Área do paralelogramo

A = base x altura

Sim para é a base e h É a altura, a área é:

A = a.h

Área de prisma hexagonal

É a soma das áreas das bases -dois hexágonos -e os dos rostos -6 retângulos ou paralelogramas-.

Área de prisma hexagonal regular

Se o prisma hexagonal tiver as bases na forma de hexágonos regulares e as bordas laterais são perpendiculares a essas bases, sua área é dada pela soma:

A = 2 x 2.5981.para² + 6º.h

Onde para É o lado do hexágono e h É a altura do prisma.

Área de prisma hexagonal irregular e reta

Se as bases são hexágonos irregulares, a área será calculada por:

A = 2a_base  + P.h

Onde:

-PARA_base É a área de base hexagonal irregular.

-P é o perímetro da base.

-H é a altura do prisma

Vértices

Cada rosto hexagonal tem 6 cantos ou vértices, o que fornece um total de 12 vértices para o prisma hexagonal.

Arestas

Há uma fórmula para encontrar o número de bordas de um prisma. Foi descoberto pelo grande matemático Leonhard Euler (1707-1783) e é chamado Teorema de Euler para poliedros. Diz assim:

Pode atendê -lo: raciocínio algébrico

Se C é o número de faces e a quantidade de vértices V e as bordas totais. É verdade que:

C+V = A+2

Os valores para o prisma hexagonal são: c = 8 e v = 12. Portanto A é:

A = c + v - 2 = 8 + 12-2 = 18

Volume

O volume V de qualquer prisma, reto ou oblíquo, de rostos regulares ou irregulares, é dado por:

V = área base x altura

Portanto, precisaremos das fórmulas para a área que vimos anteriormente.

Por exemplo, para um prisma hexagonal direto, cujas bases são hexágonos regulares, o volume é dado por:

V = 2.5981.para².h

Referências

1. Math Open Reference. Área de Polígono. Recuperado de: MathpenRef.com.
2. Wikipedia. Prisma. Recuperado de: é.Wikipedia.com.