Arquimedes Principple Fórmula, Demonstração, Aplicações

Ele Princípio de Arquimedes Ele diz que um corpo totalmente ou parcialmente submerso recebe uma força vertical chamada empurrar, que é equivalente ao peso do volume de líquido deslocado pelo corpo. 

Alguns objetos flutuam na água, outros afundam e alguns parcialmente mergulham. Para afundar uma bola de praia, é necessário fazer um esforço, porque essa força é imediatamente percebida que tenta devolvê -la à superfície. Em vez disso, uma esfera de metal afunda rapidamente. 

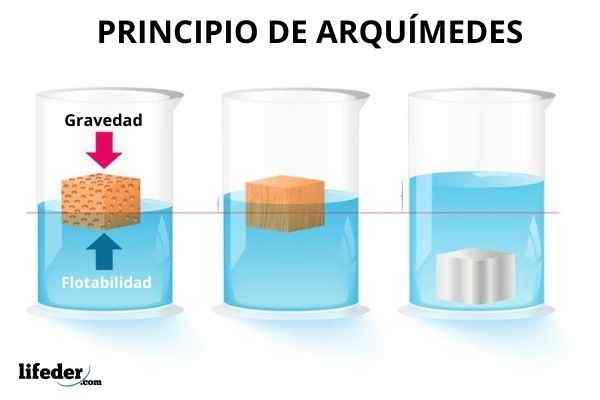
Por outro lado, objetos submersos parecem mais leves, portanto, há uma força exercida pelo fluido que se opõe ao peso. Mas você nem sempre pode compensar a gravidade. E, embora seja mais evidente com a água, os gases também são capazes de produzir essa força nos objetos imersos neles.

[TOC]

História

Arquimedes de Syracuse (287-212 A. C.) Foi quem deve ter descoberto esse princípio, sendo um dos maiores cientistas da história. Eles dizem que o rei Hierón II de Syracuse enviou um ourives para fabricar uma nova coroa, para a qual ele lhe entregou uma certa quantidade de ouro.

Arquimedes

Quando o rei recebeu a nova coroa, ele tinha o peso certo, mas ele suspeitava que o ourives o havia traído adicionando prata em vez de ouro. Como eu poderia verificar sem destruir a coroa?

Hierón chamou Archimedes, cuja fama de estudiosa era bem conhecida, para ajudá -lo a resolver o problema. A lenda afirma que Archimedes estava imerso na banheira quando encontrou a resposta e, como era sua emoção, que ele correu nu pelas ruas de Syracuse para procurar o rei gritando "Eureka", que significa "eu o encontrei".

https: // giphy.com/gifs/stito3echtlnbvliz3

O que os arquimedes encontraram? Bem, ao tomar um banheiro, o nível da água na banheira, quando ele entrou, o que significa que um corpo submerso desloca um certo volume de líquido.

E se eu submergir a coroa na água, ele também teve que mover um certo volume de água se a coroa fosse feita de ouro e diferente se fosse feita de liga com prata.

Arquimedes Princípio Fórmula

A força promocional referida no princípio de Archimedes é conhecida como empurrar hidrostático qualquer força de flutuação E, como dissemos, é equivalente ao peso do volume de fluido deslocado pelo corpo quando submerso.

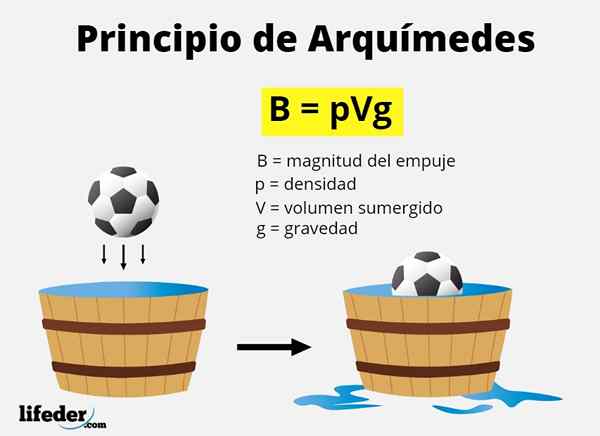
O volume deslocado é equivalente ao volume do objeto que está submerso, total ou parcialmente. Já que o peso de qualquer coisa é mg, E a massa do fluido é Densidade x volume, Negando como B à magnitude do impulso, matematicamente, tem que:

B = m_fluente x g = densidade do fluido x volume submerso x gravidade

B = ρ_fluente x v_submerso x g

Onde a letra grega ρ ("rho") denota a densidade.

O peso aparente

O peso dos objetos é calculado pela expressão bem conhecida mg, No entanto, as coisas parecem mais claras quando estão submersas na água. 

Ele peso aparente de um objeto é o que tem quando está imerso em água ou outro líquido e sabe, você pode obter o volume de um objeto irregular, como a coroa do rei Hierón, como será visto abaixo.

Pode servir a você: 13 exemplos da primeira lei de Newton na vida real

Para fazer isso, está completamente submerso na água e sujeito a uma corda presa a um dinamômetro -Um instrumento fornecido com uma mola que serve para medir as forças-. Quanto maior o peso do objeto, maior o alongamento da primavera, que é medido em uma escala fornecida no dispositivo.

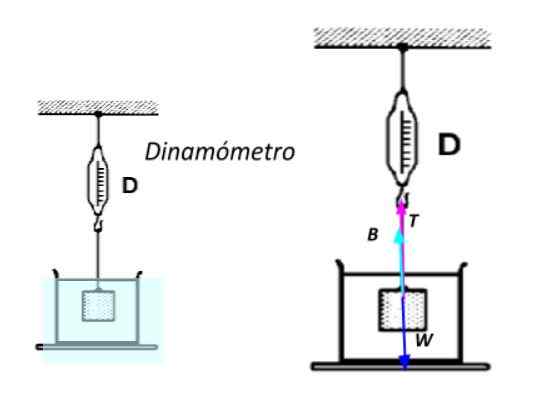Peso aparente de um objeto submerso. Fonte: preparado por f. Zapata.

Aplicando a segunda lei de Newton, sabendo que o objeto está em repouso:

Σf_e = B + T - W = 0

O peso aparente w_para É equivalente à tensão na corda T:

T = w_para

C_para = mg - ρ_fluente . V. g

Se o volume V submerso for necessário, ele será liberado como:

V = (W - W_para ) / ρ_fluente  . g

Demonstração

https: // giphy.com/gifs/mcPhppgtnpbhl4cgaq

Quando um corpo mergulha, o impulso é a força resultante de todas as forças que são exercidas no corpo através da pressão causada pelo fluido circundante:

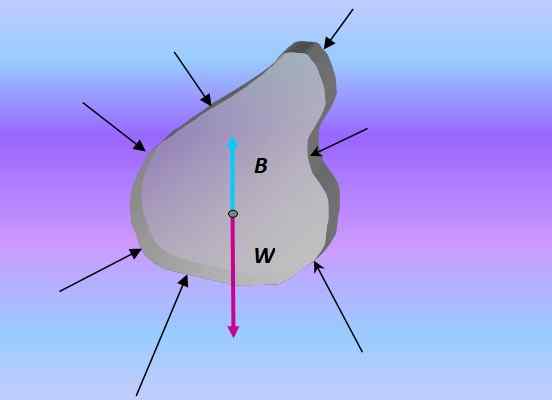Diagrama corporal livre de um objeto submerso. Fonte: preparado por f. Zapata.

Pressão e profundidade

Como a pressão aumenta com a profundidade, o resultado dessas forças é sempre direcionado verticalmente para cima. Portanto, o princípio dos arquimedes é uma conseqüência do teorema fundamental do hidrostático, que relaciona a pressão p exercida por um fluido com a profundidade z como:

P = ρ.g.z

Forças em um fluido de equilíbrio estático

Para demonstrar o princípio dos arquimedes, uma pequena porção de repouso cilíndrica é tomada em repouso para analisar as forças exercidas nele, como mostrado na figura a seguir. As forças na superfície curva do cilindro são canceladas. 

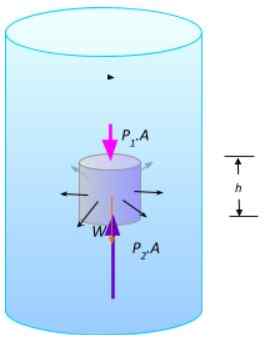Uma porção de fluido em equilíbrio. Fonte: preparado por f. Zapata.

As magnitudes das forças verticais são F₁ = P₁.A e F₂ = P2.A, há o peso C. Como o fluido está em equilíbrio, a soma das forças deve ser cancelada:

∑f_e = P₂.A- p₁.A- w = 0

P₂.A- p₁.A = w

Como o impulso compensa o peso, como a parte do fluido está em repouso, então:

B = p₂.A- p₁.A = w

A partir desta expressão, segue -se que o impulso é devido à diferença nas pressões entre a face superior do cilindro e a parte inferior. Como W = mg = ρfluente. V. g, se tem que:

B = ρ_fluente. V_submerso. g

Que é precisamente a expressão para o impulso mencionado na seção anterior.

Arquimedes Princípios Aplicações

Balões que flutuam: Arquimedes Princípio em ação

O Princípio da Arquimedes aparece em muitas aplicações práticas, entre as quais podemos nomear:

- O balão aerostático. Que, com uma densidade média menor que a do ar circundante, flutua nela devido à força de impulso.

- Os barcos. O capacete do navio é mais pesado que a água. Mas se o casco for considerado mais o ar dentro, o quociente entre a massa total e o volume é menor que o da água e é por isso que os navios flutuam.

- Os coletes salva -vidas. Quando construídos com materiais leves e porosos, eles são capazes de flutuar porque a proporção de volume de massa é menor que a da água.

- O flutuante para fechar a torneira de enchimento de um tanque de água. É uma esfera cheia de ar de grande volume que flutua sobre a água, o que causa a força de impulso - multiplicada pelo efeito da alavanca - fecha a tampa da torneira de enchimento de um tanque de água quando atingir o nível total.

Pode servir a você: ondas unidimensionais: expressão e exemplos matemáticos

Exemplos

Exemplo 1

A lenda diz que o rei Hierón deu ao ourives uma certa quantidade de ouro para fazer uma coroa, mas o monarca desconfiada achou que o ourives poderia ter traído ao colocar um metal menos valioso dentro da coroa do que a coroa. Mas como eu poderia saber sem destruir a coroa? 

O rei encomendou Archimedes e isso, procurando a solução, descobriu seu famoso princípio.

Suponha que a coroa pesa 2,10 kg-f no ar e 1,95 kg-f quando completamente submersa na água. Nesse caso, não há engano?

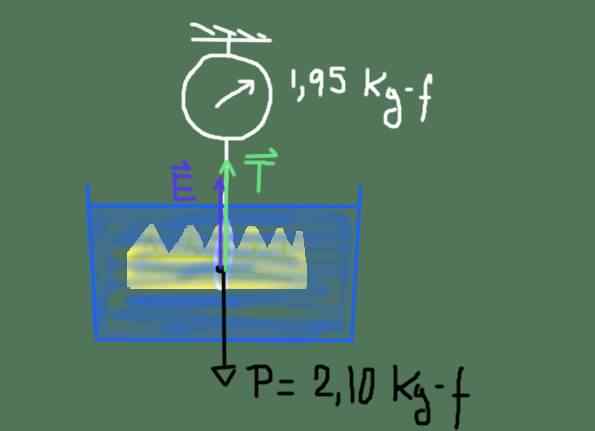Diagrama do corpo livre da coroa do rei Heron. Fonte: preparado por f. Zapata

O diagrama das forças é mostrado na figura anterior. Essas forças são: o peso P da coroa, o impulso E e a tensão T da corda que pendura na escala.

P = 2,10 kg-f e t = 1,95 kg-f é conhecido, é necessário determinar a magnitude do impulso E:

T + E = P ⇒ E = P - T = (2,10 - 1,95) kg -f = 0,15 kg -f

Por outro lado, de acordo com o princípio do Arquimedes, o impulso é equivalente ao peso da água despejada do espaço ocupada pela coroa, ou seja, a densidade da água pelo volume da coroa devido à aceleração da gravidade :

E = ρ_água⋅v⋅g = 1000 kg/m^3 ⋅ v ⋅ 9,8m/s^2 = 0,15 kg ⋅ 9,8 m/s^2

Onde o volume da coroa pode ser calculado:

V = 0,15 kg / 1000 kg / m^3 = 0,00015 m^3

A densidade da coroa é o quociente entre a massa da coroa fora da água e o volume dela:

Densidade da coroa = 2,10 kg / 0,00015 m^3 = 14000 kg / m^3

A densidade do ouro puro pode ser determinada por um procedimento semelhante e o resultado é de 19300 kg/m^3.

Comparando as duas densidades, é evidente que a coroa não é ouro puro! 

Exemplo 2 

Com base nos dados e no resultado do Exemplo 1, é possível determinar quanto ouro foi roubado pelo ourives no caso em que parte do ouro foi substituída por prata, que tem uma densidade de 10500 kg/m^3 3 3.

Vamos ligar para ρc para a densidade da coroa, ρo para a densidade de ouro e ρ_p para a densidade de prata.

A massa total da coroa é:

M = ρCC⋅v = ρo⋅vo + ρ_p⋅vp

O volume total da coroa é o volume de prata mais o volume de ouro:

V = VO + VP ⇒ VP = V - VO

Substituindo na equação de massa:

ρc⋅v = ρo⋅vo + ρ_p⋅ (V - VO) ⇒ (ρo - ρ_p) Vo = (ρc - ρ_p) V

Ou seja, o volume de ouro que contém a coroa do volume total V é:

VO = V⋅ (ρC - ρ_p)/(ρo - ρ_p) =…

… = 0,00015 m^3 (14000 - 10500)/(19300 - 10500) = 0,0000596 M^3

Para saber o peso em ouro que contém a coroa, multiplicamos Vo para a densidade do ouro:

Pode atendê -lo: regra da mão direita

MO = 19300 *0,00005966 = 1.1514 kg

Como a massa da coroa é de 2,10 kg, sabemos que 0,94858 kg de ouro foram roubados pelo ourives e substituídos por prata.

Exercícios resolvidos

Exercício 1

Um enorme balão de hélio é capaz de sustentar o equilíbrio (sem subir ou descer) para uma pessoa.

Suponha que o peso da pessoa, mais a cesta, as cordas e o balão seja de 70 kg. Qual é o volume de hélio necessário para que isso aconteça? Que tamanho o balão terá?

Solução

Assumiremos que o impulso é produzido principalmente pelo volume de hélio e que o impulso do restante dos componentes é muito pequeno em comparação com o do hélio que ocupa muito mais volume.

Nesse caso, será necessário um volume de hélio capaz de fornecer um impulso de 70 kg de peso.

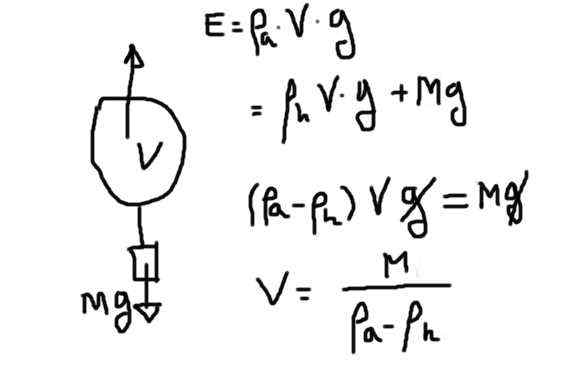Fdiaogram de corpo livre cheio de hélio. Fonte: preparado por f. Zapata.

O impulso é o produto do volume de hélio devido à densidade do hélio devido à aceleração da gravidade. Esse impulso deve compensar o peso do hélio mais o peso do resto.

Da⋅v⋅g = Da⋅v⋅g + m⋅g

onde conclui que v = m / (da - dh)

V = 70 kg / (1.25 - 0,18) kg/m^3 = 65.4 m^3

Isto é, 65 são necessários.4 m^3 de hélio à pressão atmosférica para suporte.

Se assumirmos um balão esférico, podemos encontrar o raio do mesmo da relação entre o volume e o raio de uma esfera:

V = (4/3) ⋅π⋅r^3

Onde r = 2,49 m. Em outras palavras, será necessário um diâmetro de 5 m cheio de hélio.

Exercício 2

Materiais de densidade mais baixa que flutuam na mesma. Suponha que você tenha cubos de poliestireno (cortiça branca), madeira e gelo. Suas densidades em kg por metro cúbico são respectivamente: 20, 450 e 915.

Encontre que fração do volume total está fora da água e que altura se destaca em relação à superfície da água que toma como densidade deste último 1000 kg por metro cúbico.

Solução 

A flutuabilidade ocorre quando o peso corporal é igual ao impulso devido à água:

E = m⋅g

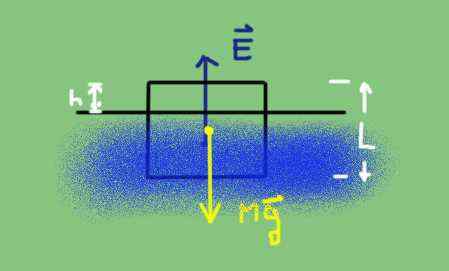Diagrama do corpo livre de um objeto parcialmente submerso. Fonte: preparado por f. Zapata.

O peso é a densidade do corpo DC multiplicada pelo seu volume V e pela aceleração da gravidade G.

O impulso é o peso do fluido deslocado de acordo com o princípio do Arquimedes e é calculado multiplicando a densidade d da água pelo volume submerso v 'e pela aceleração da gravidade.

Quer dizer que:

D⋅v'⋅g = dc⋅v⋅g

O que significa que a fração de volume submerso é igual ao quociente entre densidade corporal e densidade da água.

(V '/V) = (DC/D) 

Ou seja, a fração de volume pendente (v "/v) é

(V "/v) = 1 - (dc/d)

Sim h É a altura excepcional e eu O lado do cubo a fração de volume pode ser escrita como

(H⋅l^2)/(l^3) = h/l, Em outras palavras, a excelente fração de altura também é

(H/L) = 1 - (DC/D)

Em seguida, os resultados dos materiais solicitados são:

Polystireno (cortiça branca):

(H/l) = (v "/v) = 1 - (dc/d) = 1- (20/1000) = 98% fora da água

Madeira:

(h/l) = (v "/v) = 1 - (dc/d) = 1- (450/1000) = 55% fora da água

Gelo:

(h/l) = (v "/v) = 1 - (dc/d) = 1- (915/1000) = 8.5% fora da água

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill. 417-455.
2. Cengel Y, Cimbala J. 2011.Mecânica de fluidos. Fundamentos e aplicações. Primeira edição. McGraw Hill.
3. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 4. Fluidos e termodinâmica. Editado por Douglas Figueroa (USB). 1 - 42.
4. Giles, r. 2010. Mecânica fluida e hidráulica. McGraw Hill. 
5. Rex, a. 2011. Fundamentos da Física. Pearson. 239-263.
6. Tiptens, p. 2011. Física: conceitos e aplicações. 7ª edição. McGraw Hill.