Fórmula de pressão relativa, como é calculado, exemplos, exercícios

O Presiparente ón É o que é medido em relação a um determinado valor ou Dado, que geralmente é pressão atmosférica no nível do mar (pressão atmosférica padrão). Isso é apropriado porque grande parte das medições de pressão é realizada sob as camadas gasosas que constituem a atmosfera, que exerce sua própria pressão.

Por outro lado, a pressão absoluta é medida em relação a um vácuo total, no qual não há moléculas interagindo. Em um recipiente em que o vácuo foi feito, não há partículas atuando por dentro nas paredes ou em objetos dentro dele.

figura 1. Para medir a pressão relativa, um medidor de pressão é usado assim. Fonte: Wikimedia Commons.

As pressões medidas podem estar acima ou abaixo da pressão atmosférica. No primeiro caso, se fala do pressão do medidor E no segundo pressão de vácuo.

Normalmente, as pressões que são medidas diariamente nos pneus e na pressão arterial são pressões relativas, enquanto quando a pressão atmosférica é medida por um barômetro, é uma pressão absoluta.

[TOC]

Fórmula de pressão relativa

A pressão relativa é a diferença entre a pressão absoluta p_abdômen e pressão atmosférica p_Atm, É uma pressão ou diferença diferencial nas pressões. Na pressão relativa P_Rel É conhecido em inglês como Pressão do medidor P_g E é dado pelo relacionamento:

P_abdômen = P_Atm + P_g

P_Rel = P_abdômen - P_Atm

Para pressão, Pascal é usado como uma unidade de medida do sistema internacional de unidades, independentemente de ser uma pressão absoluta ou uma pressão relativa.

O Pascal é equivalente à força exercida por 1 Newton sobre uma área de 1 m², Mas outras unidades são usadas com frequência, como mercúrio, água, unidades anglo -saxonas, como psi as outras.

Pode atendê -lo: os 31 tipos de força na física e suas características

Como a pressão relativa é calculada?

Se a pressão absoluta for conhecida em um ponto e pressão atmosférica padrão, a pressão relativa é a subtração entre ambos.

Por exemplo, suponha que a pressão absoluta em um determinado sistema seja 305 kPa. Saber que a pressão atmosférica padrão é 101.3 kPa, a pressão relativa é:

P_g = P_abdômen - P_Atm = 305 - 101.3 kpa = 203.7 KPa

O KPA ou Kilopascal é mil vezes maior que um Pascal. É usado com mais frequência, pois os valores de pressão estão na ordem dos milhares de Pascal. O peso de uma maçã é de aproximadamente 1 Newton e um Pascional é equivalente a essa força distribuída em um quadrado lateral de 1 metro. Outros múltiplos, como Megapacal (1 mpa = 1 x 10⁶ PA) ou o Gigapascal (1 gpa = 1x 10⁹ Pa).

A pressão do exemplo é manométrica, porque está acima da pressão atmosférica, mas há pressões absolutas abaixo disso. Por exemplo, se um gás em um recipiente tiver uma pressão absoluta de 50 kPa, sua pressão relativa é uma pressão de vácuo que produz sucção:

P_g = P_abdômen - P_Atm = 50 - 101.3 kpa = -51.3 KPa

Nesses exemplos, a pressão atmosférica padrão foi usada, que é a pressão no nível do mar. Mas se for necessária mais precisão no cálculo, pode ser usada pressão atmosférica local, o que pode diferir de 101.3 KPa, pois depende da altitude e de outras condições geográficas.

Nos textos, geralmente as pressões dadas são relativas e, se for necessário trabalhar com pressões absolutas, elas são distinguidas com o uso de assinaturas para evitar confusão.

Pode servir você: sol

Variação de pressão com profundidade

Em cada ponto dentro de um fluido como a água, há pressão. Supondo que a água seja incompressível, portanto sua densidade permanece constante e a pressão varia verticalmente.

Pode ser verificado pegando uma pequena porção de fluido na forma de um disco grosso Dy Isso está em repouso no meio da massa líquida.

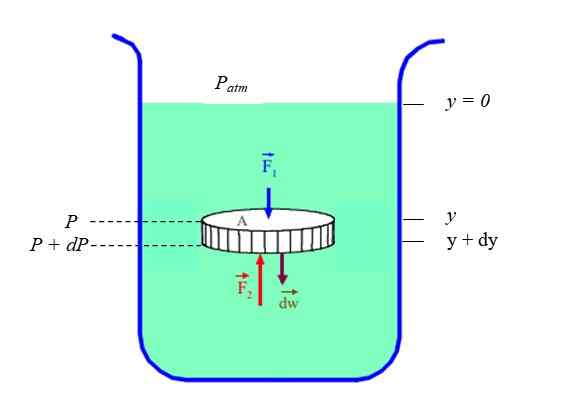Figura 2. Uma pequena porção de fluido em forma de disco, em equilíbrio estático. Fonte: f. Zapata.

As forças nas bordas circulares do disco são canceladas por pares, mas não as forças exercidas pela massa de fluido acima e abaixo do disco: F₁ e F₂. Além disso, é necessário considerar o peso do disco fluidoC Na segunda lei de Newton:

∑f_e = F₂ - F₁ - W = 0

Essas forças podem ser expressas em termos de pressão, que é a força perpendicular por unidade de área. Dessa maneira, temos a pressão p, produzida pela força f₁:

F₁ = P. PARA

Onde A é a área circular do disco. De forma similar:

F₂ = (P + dp). PARA

Com p + dp a pressão em profundidade e + dy. O peso é dw = dm . G:

(P + dp). A - p. A - dm . G = 0

A densidade do fluido é ρ = dm/ dv, com DV o volume do disco fluido, dado por um.Dy. Desta maneira:

(P + dp). A - p. A - ρa.Dy .G = 0

A equação obtida é simplificada para:

Dp - ρgdy = 0 → dp = ρgdy

Integrando os dois lados de e₁ até Y₂:

= P₂ - P₁ = ρg (e₂ - e₁)

O termo p₂ - P₁ É uma diferença nas pressões ou pressão diferencial. Se queremos saber a pressão no ponto de coordenada vertical e, nós o fazemos e₁ = 0, e₂ = y e P_qualquer = P_Atm. Com isso, teremos a pressão em relação a essa profundidade, que depende apenas da profundidade e:

Pode servir a você: Galáxia irregular: formação, características, tipos, exemplos

P₂ - P_Atm = ρgy ⇒ p_Rel = ρgy

Exemplos de pressão relativa

Pressão no fundo de uma piscina

Todos nós experimentaram a pressão que é sentida mergulhando em uma piscina ou no mar. Qual é a pressão relativa sentida por ser submerso em uma piscina de água doce a 5 metros de profundidade? Usando a expressão anterior e saber que a densidade da água doce é de 1000 kg/m³, Com g = 9.81 m/s² A pressão relativa é:

P_Rel = ρgy = 1000 x 9.81 x 5 Pa = 49050 Pa.

Pressão sobre um pneu

Os pneus de veículo geralmente estão sob uma pressão de 32 psi. Esta é uma pressão relativa ou manométrica em libras por polegada quadrada, a unidade usada em países de língua inglesa. Muitos manômetros são calibrados nessas unidades. 32 PSI é igual a 220632 PA O 220 KPA.

Exercício resolvido

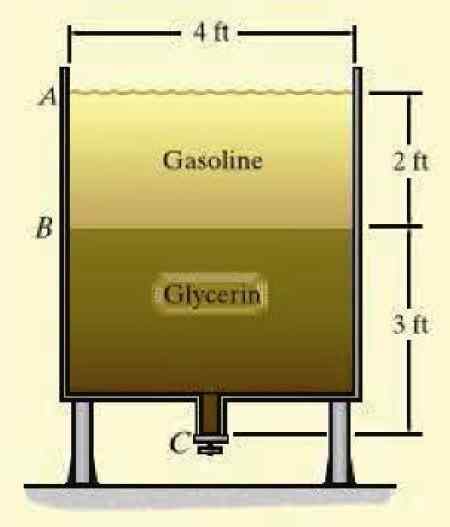
Um tanque contém gasolina e glicerina, dois líquidos não disciplistas (não misturam) nas alturas indicadas. Qual é a pressão manométrica no fundo do tanque? Os pesos específicos são anexados, indicados com a letra grega γ, de cada fluido:

γ_gás = 45.3 lb/ft³

γ_Gly = 78.7 lb/ft³

Figura 3. Um tanque cheio com dois líquidos não disciplinados. Fonte: Hibbeler, r. Mecânica de fluidos.

Solução

O peso específico γ de um fluido é o produto de sua densidade devido à aceleração da gravidade; portanto, a equação da pressão relativa pode ser expressa da seguinte maneira:

P_Rel = γ.e

A pressão relativa no fundo do tanque é devido ao peso da coluna de glicerina e à da gasolina e é independente da forma do tanque:

P_Rel = γ_gás . e_Ab + γ_Gly . e_Bc = (45.3 x 2 + 78.7 x 3) lb/ft² = 326.7 lb/ft²

Referências

1. Cimbala, c. 2006. Mecânica de fluidos, fundamentos e aplicações. Mc. Graw Hill.
2. Hibbeler, R. 2015. Mecânica de fluidos. 1º. Ed. Pearson.
3. Mott, r.  2006. Mecânica de fluidos. 4º. Edição. Pearson Education.
4. Senta, a. 2006. Mecânica de fluidos, uma introdução física. Alfa Ômega.
5. Streeter, v. 1999. Mecânica de fluidos. McGraw Hill.
6. Zapata, f. Pressão e profundidade. Recuperado de: Francesphysics.Blogspot.com.