Fórmula de pressão hidrostática, cálculo, exemplos, exercícios

O Pressão hidrostática É aquele que exerce um fluido em equilíbrio estático em qualquer lugar, uma área imersa nele, as paredes do recipiente ou uma porção de fluido que faz parte da massa total.

A maneira pela qual os fluidos exercem pressão difere dos sólidos. Eles exercem pressão para baixo, mas um líquido ou um gás o fazem em todas as direções.

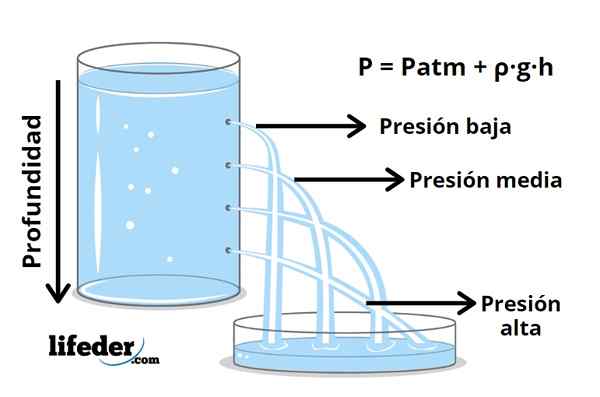
Figura 1- a maior profundidade de pressão

Quando se trata de um líquido, a pressão aumenta com a profundidade, como é conhecido pela experiência ao imergir na água em que o aumento da pressão é sentido nos ouvidos. Essa pressão vem do peso do fluido e do movimento incessante das partículas que o compõem, que atingem continuamente a superfície do corpo imerso no fluido.

Se assumirmos um líquido incompressível - o que é verdadeiro na grande maioria das aplicações - sua densidade permanece constante e, nesse caso, a pressão depende linearmente da profundidade.

[TOC]

Fórmula

A pressão hidrostática é calculada pela seguinte expressão:

P = p_Atm + ρ · g · h

Onde:

-P A pressão exercida em um ponto

-P_Atm É a pressão da atmosfera na superfície livre

-ρ é densidade de fluido

-G é a aceleração da gravidade

-H é a profundidade em que você deseja calcular a pressão hidrostática 

A fórmula inclui os efeitos da atmosfera, mas muitas pressão ou manômetros colocam 0 na pressão atmosférica, por esse motivo o que eles medem é a pressão diferencial ou a pressão relativa, também chamado pressão do medidor:

P_m = ρ · g · h

Quanto aos gases, eles são compactados ou expandidos com muita facilidade. Portanto, sua densidade, que é a razão entre massa e volume, geralmente é uma função de outros parâmetros, como altitude e temperatura, no caso de gases atmosféricos.

Pode servir a você: Magnetização: Orbital e Moment Magnético, Exemplos

A pressão que os gases exercem geralmente é chamada pressão aerostática, o termo pressão hidrostática para líquidos sendo reservados.

Exemplos de pressão hidrostática

A pressão hidrostática depende apenas da profundidade; portanto, a forma ou área da base do recipiente não é relevante.

Como a pressão P é definida como o componente perpendicular da força F por unidade da área A:

P = f/a

Em seguida, a força exercida pelo líquido no fundo de um recipiente pode ser diferente, mas ser distribuído por diferentes extensões, a pressão, que é a proporção de força/área, é a mesma para pontos para a mesma profundidade.

Considere os recipientes da figura. A pressão é a mesma para todos os pontos vermelhos que estão no mesmo nível, embora haja uma quantidade maior de fluido acima desse nível no recipiente central -mais largura -, da qual existe o tubo cilíndrico e fino da extrema esquerda esquerda.

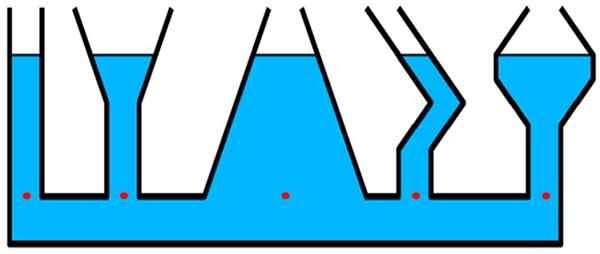Figura 2.- A pressão em qualquer um dos pontos vermelhos é a mesma, independentemente da forma do recipiente. Fonte: Wikimedia Commons.

Estruturas onde a pressão hidrostática é relevante

-As paredes de uma barragem: embora a força seja a mesma para todos os pontos do fundo plano, na parede vertical cresce à medida que a profundidade aumenta, de modo que os muros de contenção são mais largos na base do que na parte superior.

-Nas paredes e no fundo de uma piscina.

-Em estrelas como nosso sol, onde a pressão hidrostática equilibra a força da gravidade e mantém a estrela em operação. Quando o referido equilíbrio é quebrado, a estrela entra em colapso e sofre mudanças extremas em sua estrutura.

Pode atendê -lo: qual é o momento magnético?

-Tanques de armazenamento líquido, projetados para resistir à pressão hidrostática. Não apenas as paredes, mas os portões que facilitam o preenchimento e a extração. Por seu design, ele é levado em consideração se o líquido for corrosivo e também a pressão e força que exerce de acordo com sua densidade.

-Pneus e balões, que são infectados de tal maneira que resistem à pressão do líquido (gás ou líquido) sem rasgar.

-Qualquer corpo submerso, que experimenta um impulso vertical, ou "alívio" de seu peso, graças à pressão hidrostática exercida pelo líquido. Isso é conhecido como o Princípio de Arquimedes.

Exercícios

O Princípio da Arquimedes afirma que, submergindo um corpo, total ou parcialmente, ele experimentará uma força vertical para cima, conhecida como impulso. A magnitude do impulso é numericamente igual ao peso do volume de água deslocado pelo objeto.

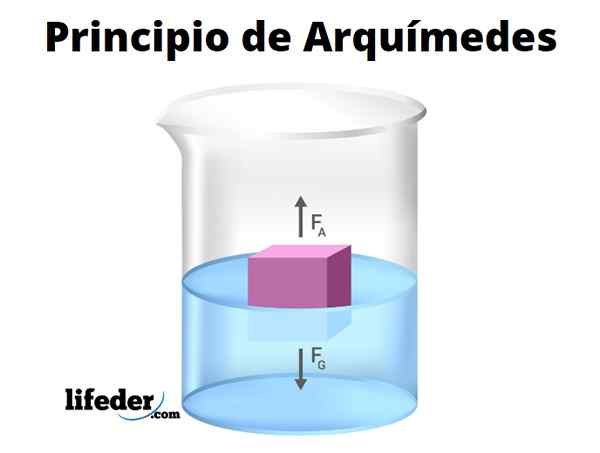
Ser ρ_fluente A densidade do fluido, v_s O volume submerso, g A aceleração da gravidade e B a magnitude do impulso, que podemos calcular pela seguinte expressão:

B = ρ_fluente .V_s .g

- Exercício 1

Um bloco retangular cujas dimensões são 2.0 cm x 2.0 cm x 6.0 cm flutua em água fresca com seu eixo vertical mais longo. O comprimento do bloco que se destaca acima da água é 2.0 cm. Calcule a densidade do bloco.

Solução

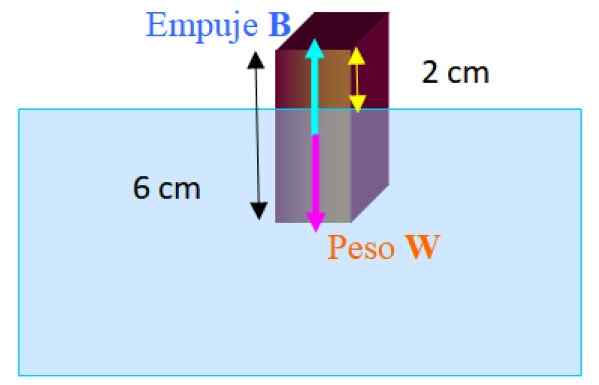Figura 3.- Diagrama do corpo livre para o bloco que flutua parcialmente submerso na água. Fonte: f. Zapata.

As forças que atuam no quarteirão são o peso C para baixo e empurrar B até em cima. À medida que o bloco flutua em equilíbrio que você tem:

∑ f_e = B - w = 0

B = w

A magnitude do peso w é o produto da massa m do bloco devido à aceleração da gravidade. Usaremos a definição de densidade ρ_qualquer Como o quociente entre a massa m e o volume V do bloco:

Pode atendê -lo: Análise de Mesheal: Conceitos, Métodos, Exemplos

ρ_qualquer = m / v → m = ρ_qualquer . V

Por sua parte, o impulso é:

B = ρ_fluente .V_s .g

Magnitude de equalização do impulso e magnitude do peso:

ρ_fluente .V_s .G = ρ_qualquer . V.g

A gravidade é cancelada por ser um fator de ambos os lados e a densidade do bloco pode ser limpa como:

ρ_qualquer = ρ_fluente . (V_s  / V)

A densidade da água em unidades de sistema internacional é de 1000 kg/m³. Volumes V Total e Submerso V_s, Eles são calculados por v = largura x alta x profundidade:

V = 2.0 cm x 2.0 cm x 6.0 cm = 24.0 cm³

V_s = 2.0 cm x 2.0 cm x 4.0 cm = 16.0 cm³

Substituindo valores:

ρ_qualquer = ρ_fluente . (V_s  / V) = 1000 kg/ m³ . (16/24) = 667 kg/m³

- Exercício 2

Calcule a porcentagem de volume submerso de um pedaço de gelo flutuando em água do mar a 0 ºC.

Solução

O gelo flutua na água, pois sua densidade é menor: 916.8 kg/m³, o que significa que ele se expande quando esfria, diferente da maioria das substâncias, que quando aquecem, aumentam seu volume.

Figura 4. Quase todo o volume de um iceberg permanece submerso. Fonte: Pixabay.

É uma circunstância muito afortunada para a vida, desde então as massas de água congelam apenas na superfície, restante líquido na profundidade.

A densidade da água do mar é um pouco maior que a da água fresca: 1027 kg/m³. Vamos calcular a fração de volume v_s  / V:

V_s  / V = ​​ρ_qualquer / ρ_fluente = 916.8 kg/m³  / 1027 kg/ m³ = 0.8927

Isso significa que aproximadamente 89 % do gelo permanece submerso sob água. Apenas 11 % é visível flutuando no mar.

Referências

1. Giambattista, a. 2010. Física. 2º. Ed. McGraw Hill.
2. Cavaleiro, r.  2017. Física para cientistas e engenharia: uma abordagem de estratégia. Pearson.
3. Cimbala, c. 2006. Mecânica de fluidos, fundamentos e aplicações. Mc. Graw Hill.
4. Hibbeler, R. 2015. Mecânica de fluidos. 1º. Ed. Pearson.
5. Mott, r.  2006. Mecânica de fluidos. 4º. Edição. Pearson Education.
6. Streeter, v. 1999. Mecânica de fluidos. McGraw Hill.