Perímetro do círculo Como tirá -lo e fórmulas, exercícios resolvidos

Ele perímetro do círculo É o conjunto de pontos que formam o contorno de um círculo e também é conhecido como comprimento da circunferência. Depende do raio, pois uma circunferência maior obviamente terá um contorno maior.

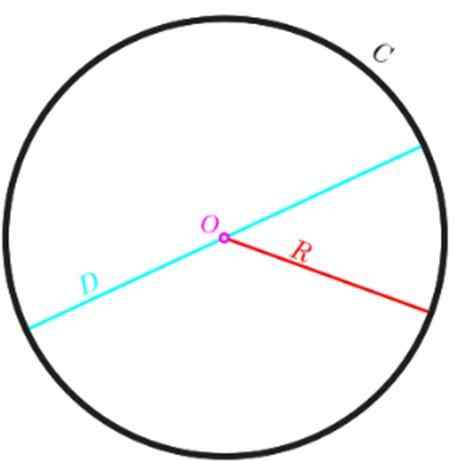
Ser P O perímetro de um círculo e R o raio do mesmo, então podemos calcular P Com a seguinte equação:

P = 2π.R

O perímetro do círculo (neste caso uma pizza) depende de seu rádio. Fonte: Pixabay.

Onde π é um número real (diz "pi") que vale aproximadamente 3.1416… os pontos suspeitos são devidos ao fato de π ter decimais infinitas. Portanto, ao fazer os cálculos, é necessário arredondar seu valor.

No entanto, para a maioria das aplicações, basta levar o valor indicado aqui ou usar todas as decimais que a calculadora com a qual funciona.

Se, em vez de ter o raio, é preferido usar o diâmetro d, o que sabemos que é o dobro do raio, o perímetro é expresso da seguinte forma:

P = π.2r = π.D

Como o perímetro é um comprimento, sempre deve ser expresso em unidades como medidores, centímetros, pés, polegadas e mais, dependendo do sistema que é preferido.

[TOC]

Circunferências e círculos

Geralmente são termos usados ​​de forma intercambiável, ou seja, como sinônimos. Mas acontece que existem diferenças entre eles.

A palavra "perímetro" vem do período grego "que significa contorno e" metrô "ou medida. A circunferência é o contorno ou perímetro do círculo. Formalmente, está definido:

Uma circunferência é o conjunto de pontos com distância igual a um ponto chamado centro, sendo essa distância o raio da circunferência.

Por sua parte, o círculo é definido da seguinte forma:

Um círculo é o conjunto de pontos cuja distância até um ponto chamado centro é menor ou igual a uma distância fixa chamada rádio.

O leitor pode alertar a diferença sutil entre os dois conceitos. A circunferência refere -se apenas ao conjunto de pontos de borda, enquanto o círculo é o conjunto de pontos da borda para o interior, do qual a circunferência é a borda.

Pode atendê -lo: exercícios de liberação de fórmula

Exercícios de dEmostração do cálculo do perímetro do círculo

Através dos exercícios a seguir, os conceitos descritos serão colocados em prática, assim como alguns outros que serão explicados à medida que aparecem. Começaremos do mais simples e o grau de dificuldade será aumentado progressivamente.

- Exercício 1

Encontre o perímetro e a área do círculo de rádio de 5 cm.

Solução

A equação dada no início é aplicada diretamente:

P = 2π.R= 2π.5 cm = 10 π cm = 31.416 cm

Para calcular a área PARA A fórmula a seguir é usada:

PARA = π.R² = π. (5cm)²= 25π cm²= 78.534 cm²

- Exercício 2

a) Encontre o perímetro e a área da região em branco da figura a seguir. O centro do círculo sombreado está no ponto vermelho, enquanto o centro da circunferência branca é o ponto verde.

b) Repita a seção anterior para a região sombreada.

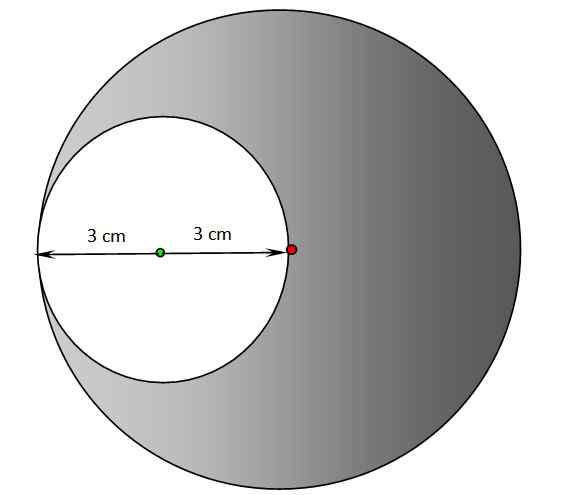Círculos para o Exercício 2. Fonte: f. Zapata.

Solução

a) O raio da circunferência branca é de 3 cm; portanto, aplicamos as mesmas equações do Exercício 1:

P = 2π.R= 2π.3 cm = 6 π cm = 18.85 cm

PARA = π.R² = π. (3cm)²= 9π cm²= 28.27 cm²

b) Para o círculo sombreado, o raio é de 6 cm, seu perímetro é o dobro do calculado na Seção A):

P = 2π.R= 2π.6 cm = 12 π cm = 37.70 cm

E, finalmente, a área da região sombreada é calculada da seguinte forma:

- Primeiro é a área do círculo sombreado como se estivesse completo, que chamaremos de ', assim:

PARA' = π.R²= π.(6 cm)² = 36π cm²= 113.10 cm²

- Então para a área PARA' A área do círculo branco é subtraído, previamente calculado na seção A), dessa maneira, a área solicitada é obtida, que será indicada simplesmente como:

A = a ' - 28.27 cm² = 113.10-28.27 cm² = 84.83 cm²

- Exercício 3

Encontre a área e o perímetro da região sombreada na figura a seguir:

Pode servir a você: ângulos suplementares: o que são, cálculo, exemplos, exercícios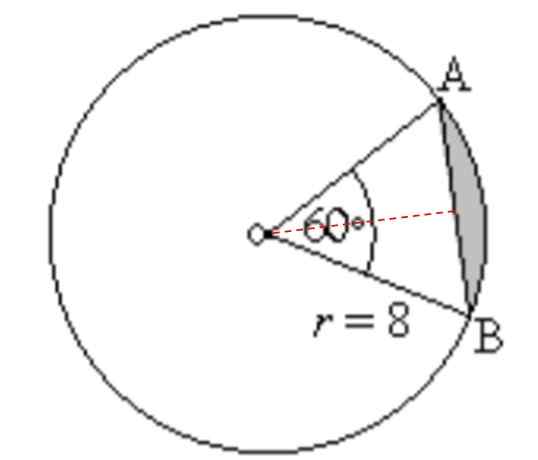Figura para o Exercício 3. Fonte: f. Zapata.

Solução

Cálculo da área da região sombreada

Primeiro calculamos a área do Setor circular ou cunha, entre os segmentos retos OA e OB e o segmento AB circular, como mostrado na figura a seguir:

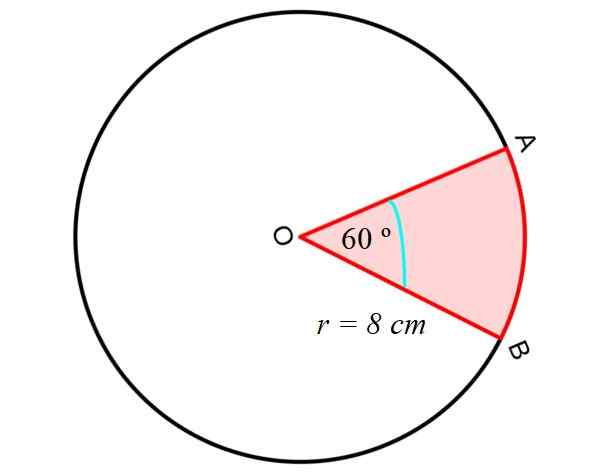
Para isso, a equação a seguir é usada, o que nos dá a área de um setor circular, conhecendo o raio r e o ângulo central entre os segmentos OA e OB, ou seja, dois dos rádios da circunferência:

PARA _{Setor circular} = Π.R². (αº/360º)

Onde αº é o ângulo central - é central porque seu vértice é o centro da circunferência - entre dois rádios.

Etapa 1: Cálculo da área do setor circular

Dessa maneira, a área do setor mostrada na figura é:

PARA _{Setor circular} = Π.R². (αº/360º) = π. (8 cm)². (60º/360º) = (64/6) π cm²= 33.51 cm²

Etapa 2: Cálculo da área do triângulo

Em seguida, calcularemos a área do triângulo branco da Figura 3. Este triângulo é equilateral e sua área é:

PARA _triângulo = (1/2) base x altura

A altura é a linha vermelha pontilhada vista na Figura 4. Para encontrá -lo, você pode usar o teorema de Pitágoras, por exemplo. Mas não é o único caminho.

O leitor de observador terá notado que o triângulo equilátero é dividido em dois retângulos idênticos, cuja base é de 4 cm:

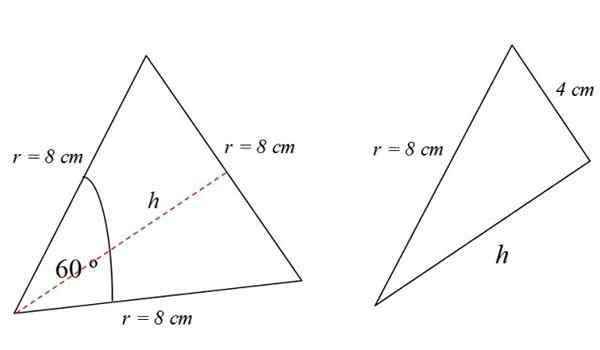
No triângulo direito, o teorema de Pitágoras é cumprido, portanto:

Como você tem a altura do triângulo, ambos do retângulo e do equilátero, sua área é calculada:

PARA _triângulo = (1/2) base x altura = (1/2) 8 cm x 6.93 cm = 27.71 cm².

Etapa 3: Cálculo da área sombreada

É suficiente subtrair a área principal (a do setor circular) da área menor (a do triângulo equilátero): a _{região sombreada} = 33.51 cm² - 27.71 cm² = 5.80 cm².

Cálculo do perímetro da região sombreada

O perímetro pesquisado é a soma do lado retilíneo de 8 cm e o arco de circunferência AB.  No entanto, a circunferência completa subtende 360 ​​º, portanto, um arco que subthes 60 º é uma sexta parte do comprimento total, o que sabemos que é 2.π.A:

Pode atendê -lo: função crescente: como identificá -lo, exemplos, exercícios

AB = 2.π.R / 6 = 2.π.8 cm / 6 = 8.38 cm

Substituindo, o perímetro da região sombreada é:

P = 8 cm + 8.38 cm = 16.38 cm.

Formulários

O perímetro, como a área, é um conceito muito importante na geometria e com muitas aplicações na vida cotidiana.

Artistas, designers, arquitetos, engenheiros e muitas outras pessoas usam o perímetro enquanto desenvolvem seu trabalho, especialmente o de um círculo, já que a forma redonda está por toda parte: da publicidade, da comida a máquinas.

A circunferência e o círculo estão entre as geometrias mais usadas. Fonte: Pixabay.

Para conhecer diretamente o comprimento de um círculo, basta embrulhá -lo com um fio ou string, estender este fio e medi -lo com uma fita adesiva. A outra alternativa é medir o raio ou diâmetro do círculo e usar algumas das fórmulas descritas acima.

No trabalho diário, o conceito de perímetro é usado quando:

-O molde apropriado é escolhido para uma certa pizza ou tamanho de bolo.

-Uma estrada urbana será projetada, calculando o tamanho de um redoma onde os carros podem se transformar para mudar o significado.

-Sabemos que a Terra gira em torno do sol em uma órbita aproximadamente circular -na realidade das órbitas planetárias são elípticas, de acordo com as leis de Kepler -mas a circunferência é uma abordagem muito boa para a maioria dos planetas.

-O tamanho apropriado de um anel ou anel que será comprado em uma loja online é escolhido.

-Escolhemos uma chave para o tamanho certo para soltar uma noz.

E muitos mais.

https: // youtu.Be/cr8xjryl5tk

Referências

1. Tutoriais de matemática gratuitos. Área e perímetro de um círculo - calculadora de geometria. Recuperado de: analisath.com.
2. Math Open Reference. Circunferência, perímetro de um círculo. Recuperado de: MathpenRef.com.
3. Instituto Monterey. Perímetro e área. Recuperado de: MontereyInstitute.org.
4. Cienting. Como encontrar o perímetro de um círculo. Recuperado de: cienting.com.
5. Wikipedia. Circunferência. Recuperado de: em.Wikipedia.org.