Conceito, tipos e exemplos de ondas tridimensionais

São ondas tridimensionais Aqueles que se espalharam no espaço, por exemplo, a onda sonora produzida por um alto -falante. Essa onda se espalha em todas as direções, embora não com a mesma intensidade em todos eles.

Se ocorrer um distúrbio em um ponto do espaço, ele se espalha nas três direções espaciais, as frentes de onda frontal sendo fechadas, esféricas, elípticas ou algum outro tipo.

Ondas tridimensionais produzidas por um orador

Por outro lado, se o local onde as ondas se originarem, ou seja, a fonte tem uma distribuição plana, então o distúrbio viajará principalmente na direção perpendicular a esse plano, formando frentes de onda plana.

[TOC]

Tipos de ondas tridimensionais

Nas ondas tridimensionais, as frentes de ondas são um conjunto de superfícies imersas no espaço tridimensional.

Agora, a frente das ondas é o local geométrico dos pontos espaciais que são alcançados pelo distúrbio inicial, ao mesmo tempo.

Três tipos de ondas que viajam no espaço tridimensional são geralmente consideradas, de acordo com a simetria da frente da onda: ondas planas, ondas cilíndricas e ondas esféricas. No entanto, ondas reais nem sempre pertencem a esses tipos, porque não têm um grau tão alto de simetria.

Ondas planas

Uma onda plana que viaja na direção positiva do X rapidamente V, é funcionalmente representada como:

G (x, t) = f (x - v⋅t)

Esta onda não se limita ao eixo x, mas também se estende nos endereços e e z. Mas a forma funcional indica que todos os pontos que têm a mesma coordenada X, independentemente das coordenadas (z, y), têm o mesmo valor G.

Nesse caso v, Significando isso que a onda plana ocupa o espaço tridimensional tridimensional.

A expressão que representa uma onda plana que se espalha em qualquer direção ou rapidamente v, onde ou representa uma unidade de diretores vetores sênior cos (α), cos (β) e cos (γ), é:

Pode servir a você: entalpia de reação: definição, termoquímica, exercícios

g = f (û • r - V⋅t) = f (x cos (α) + e cos (β) + z cos (γ) - v⋅t)

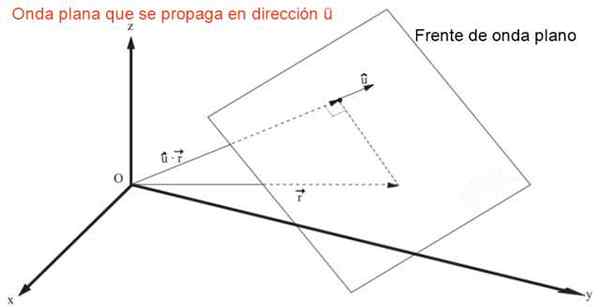Front plana que se espalha no espaço tridimensional rapidamente v. Fonte: f. Zapata.

É fácil demonstrar, por substituição direta, que a expressão anterior é uma solução da equação de onda tridimensional, uma equação em derivados parciais da segunda ordem linear:

∂_XxG + ∂_AAG + ∂_ZZG = (1/V²) ∂_Ttg

A equação anterior pode ser escrita de forma mais compacta usando o operador Laplacian ∇²:

∇²G = (1/V²) ∂_Ttg

Ondas cilíndricas

Quando o distúrbio inicial é distribuído sobre uma linha reta, a onda se espalha na direção radial perpendicular àquela linha que preenche o espaço tridimensional que o rodeia, com frentes de onda cilíndrica.

Ondas esféricas

Quando a fonte é pontual e o meio em que a onda tridimensional é propagada é homogênea e isotrópica (suas propriedades não mudam de acordo com a direção), as frentes de onda são esferas concêntricas ao ponto em que o distúrbio inicial ocorreu.

No caso de uma onda esférica na qual a intensidade da onda é idêntica em todas as direções, a função que descreve o distúrbio depende apenas da distância r para a fonte oportuna e de tempo t.

Nesse caso, o Laplaciano correspondente é:

∇²G = (1/r²) ∂_r(r² ∂_rg)

Sendo a equação da onda:

∇²G = (1/V²) ∂_Ttg

A solução geral seria:

g (r, t) = (1/r) f (r - v⋅t) + (1/r) g (r + v⋅t)

Neste caso, diz -se que é um onda esférica. Mas pode haver variantes, como será visto abaixo

Ondas esféricas não isotrópicas

Também pode acontecer que uma onda esférica, isto é, com as frentes de onda formadas por esferas concêntricas para um ponto central, a amplitude ou intensidade da onda é diferente nas diferentes direções.

É o que acontece quando a fonte central da onda é mais eficiente em uma direção do que outros. 

Pode servir a você: Física antes dos gregos (Antígua Grécia)

Por exemplo, o som produzido por uma buzina não tem a mesma intensidade em todos os lugares, mesmo no caso de pontos equidados.

A intensidade não é a mesma, embora o sinal leve o mesmo tempo para alcançar esses pontos. É uma onda esférica que possui um padrão direcional não esférico. 

Também existem ondas esféricas no caso de ondas eletromagnéticas criadas por uma antena, mas elas podem não ser igualmente intensas em todas as direções.

Antena do transmissor

Metade não -homogênea

Quando o meio não é homogêneo, a velocidade de propagação da onda é diferente em direções diferentes.

Um exemplo de meio não -homogêneo é a atmosfera em que há diferenças de pressão com a altura e há gradientes de temperatura. Outro exemplo é os estratos da crosta terrestre, que diferem em densidade e módulo elástico. 

A não homogeneidade resulta nas frentes de ondas originárias de uma fonte pontual central não são esferas concêntricas, uma vez que a distância percorrida pela onda, no mesmo período de tempo, é diferente em cada direção.

Depois, há uma onda tridimensional cuja frente de onda não é esférica.

Intensidade e energia de uma onda esférica

Podemos escrever a expressão de uma onda harmônica esférica assim:

g (r, t) = (g_qualquer / r) cos (k⋅r - ω⋅t)

Onde as frentes de onda se espalham rapidamente igual a:

V = ω/k

E sua amplitude diminui com o inverso da distância r da fonte pontual de ondas esféricas.

Ondas harmônicas têm densidade energética (Energia por unidade de volume) ε dado por:

ε = ½ ρ ω² (g_qualquer / r)²

Nesta equação:

-ρ Possui unidades de massa por unidade de volume e representa a densidade do meio, onde uma onda sonora se propaga.

-g_qualquer É a amplitude do deslocamento de um elemento do meio, por exemplo, um fluido, devido à onda de propagação.

Pode atendê -lo: atrito viscoso (força): coeficiente e exemplos

Deve -se notar que, como é uma onda esférica, a densidade de energia diminui com o inverso do quadrado da distância.

A intensidade da onda, ou seja, a energia transmitida por unidade de tempo é:

I = v⋅ε

Como sempre, na prática, a magnitude mais importante é a energia transmitida por unidade de área para distância radial r:

P = v⋅ε = i_qualquer / r²

Ser Yo_qualquer = ½ ρ v ω² g_qualquer².

A energia total transmitida por unidade de tempo através de um raio r é:  P⋅4πr²= 4π⋅i_qualquer, E como esperado, não depende da distância radial. 

Exemplos de ondas tridimensionais

As ondas tridimensionais são muito frequentes, então temos:

Antenas emissoras de ondas eletromagnéticas

As ondas produzidas por uma antena ou o som produzido por um braço são ondas tridimensionais, embora de natureza diferente

Eles cobrem um espectro muito amplo, desde as ondas de rádio entre as centenas de KHz e centenas de MHz, até as ondas emitidas pela antena da antena Wi-fi da ordem do GHZ, que já cai na gama de microondas. 

Sabemos que o microondas, embora não sejam uma radiação ionizante, eles são capazes de aumentar a temperatura do organismo porque contém muita água.

Portanto, não é aconselhável ter a antena Wi-Fi perto da cabeça ou corpo. Basta fugir um pouco, pois a uma distância dupla, a intensidade é um quarto.

Ondas sísmicas

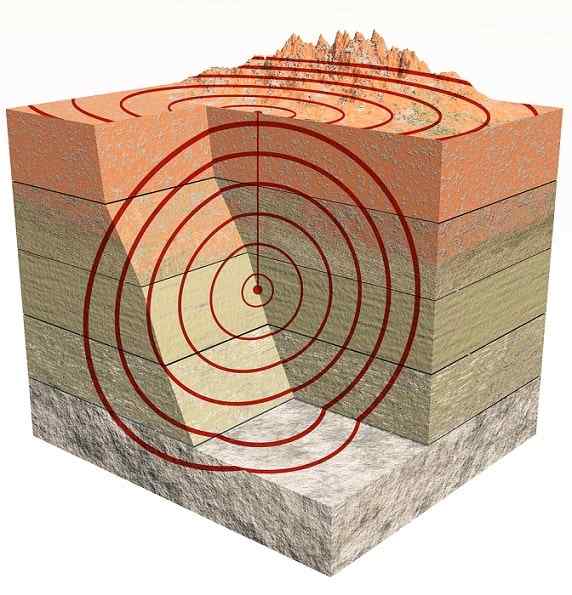Ondas sísmicas

Eles também são ondas tridimensionais. Principalmente existem aqueles do tipo P quais são ondas de compressão e tipos S O que são cortar ou cisalhamento (sOuvir em inglês).

As ondas P ou primário são os primeiros a chegar porque se espalham a um mais rápido que as ondas S ou secundário.

O som

Som falando

O som é um tipo de onda tridimensional. Essas ondas se espalharam em todas as direções, embora, como já dissemos antes, não com a mesma intensidade em todas as direções.

Isso ocorre porque a fonte de som nem sempre emite com simetria perfeitamente esférica.

Referências

1. Baranek, l. 1969. Acústica. 2º. Edição. McGraw Hill.
2. Griffiths g. Ondas lineares e não lineares. Recuperado de: Scholarpedia.org.
3. Nottoli, h. 2004. Física aplicada à arquitetura. Nobuko.
4. Whitham g.B. 1999. Ondas lineares e não lineares. Wiley. 
5. Wikiwaves. Ondas não lineares. Recuperado de: wikiwaves.org