Ondas estacionárias fórmulas, características, tipos, exemplos

As ondas em pé São ondas que se espalham em uma metade limitada, indo e entrando em uma parte do espaço, ao contrário das ondas de viagem, que ao propagação se afastam da fonte que os originou e não retorna a ele.

Eles são a base dos sons produzidos nos instrumentos musicais, uma vez que surgem facilmente nas cordas fixas, em um de suas extremidades ou em ambos. Eles também são criados em membranas tensas, como bateria ou tubos internos e estruturas, como pontes e edifícios.

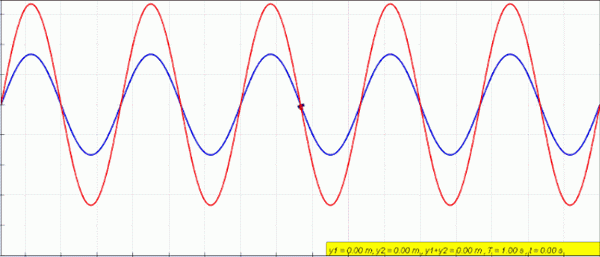Animação de uma onda estacionária (vermelha) criada pela superposição de uma onda esquerda (azul) e direita (verde). Fonte: LookanngMany Agradecimentos ao autor da simulação original = Wolfgang Christian e Francisco Schembre Autor da simulação Easy Java = Francisco Schembre/CC BY-SA (https: // criativo.Org/licenças/BY-SA/4.0)

Quando você tem uma corda fixa nas duas extremidades, como um violão, por exemplo, ondas são criadas com amplitude e frequência idênticas, que viajam em sentidos opostos e combinam produzindo um fenômeno chamado interferência.

Se as ondas estiverem em fase, os cumes e vales estão alinhados e resultam em uma onda com amplitude dupla. Nesse caso, se fala em interferência construtiva.

Mas se as ondas que interferem estão fora de fase, as cristas de um atendem aos vales de outros e a amplitude que resulta é zero. É então uma interferência destrutiva.

[TOC]

Fórmulas e equações

Os principais elementos da onda para representá -lo no espaço e no tempo são sua amplitude a, seu comprimento de onda λ e sua frequência angular ω.

Elementos de uma onda. Fonte: Wikimedia Commons.

Em representação matemática, é preferido usar k do que o Número da onda o Número de vezes que a onda por unidade está acontecendo. É por isso que é definido através do comprimento da onda λ, que é a distância entre dois vales ou duas cristas:

K = 2π/ λ

Enquanto o frequência angular Está relacionado ao período ou duração de uma oscilação completa, como:

Ω = 2π/ t

E também a frequência f é dada por:

F = ω / 2π

Portanto:

F = 1/t

Além disso, as ondas se movem com velocidade v de acordo com:

v = λ.F

Expressão matemática da onda estacionária

Matematicamente, podemos expressar uma onda através da função sinusal ou da função cosseno. Suponha que haja ondas de amplitude igual a, comprimento de onda λ e frequência ω, espalhando -se ao longo de uma corda e em sentidos opostos:

e₁ = Um sin (kx - ωt)

e₂ = Um sin (kx + ωt)

Ao adicioná -los, encontramos a onda resultante e_R:

e_R = y₁ + e₂ = Um sen (kx - ωt) + um sin (kx + ωt)

Há uma identidade trigonométrica para encontrar a soma:

Pode atendê -lo: o que é relativa e absoluta aspereza?

sin α + sin β = 2 sin (α + β)/2 . cos (α - β)/2

Através dessa identidade, a onda resultante e_R é sobrou:

e_R = [2a sen kx] . cos ωt

Localização de nós e barriga

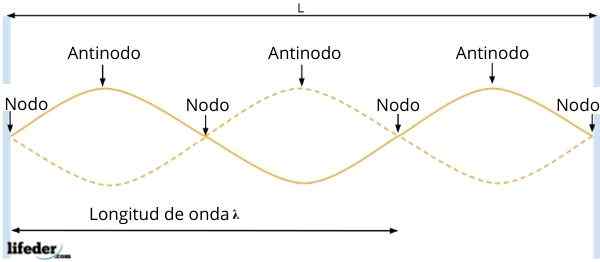Antinodos ou barrigas e nós

A onda resultante tem amplitude para_R = 2ase kx, que depende da posição da partícula. Então, nos pontos em que sen kx = 0, a amplitude da onda é cancelada, ou seja, não há vibração.

Esses pontos são:

Kx = π, 2π, 3π ..

Como k = 2 π/ λ:

(2 π/ λ) x = π, 2π, 3π ..

x = λ/2, λ, 3λ/2 ..

Em tais pontos, ocorre interferência destrutiva e eles são chamados nós. Eles são separados por uma distância igual a λ/2, deduzida do resultado anterior.

E entre dois nós consecutivos estão os antinodos ou barriga, em que a amplitude da onda é máxima, uma vez que a interferência construtiva ocorre. Eles ocorrem quando:

sin kx = ± 1

Kx = ± π/2, 3π/2, 5π/2 ..

Novamente k = 2 π/ λ e depois:

x = λ /4, 3λ /4, 5λ /4, ..

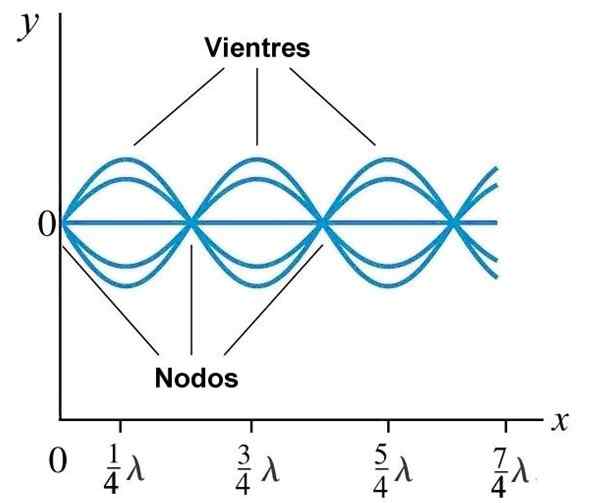Barriga ou antinodos e nós em uma onda estacionária gerada em uma corda com extremidade fixa em x = 0. Fonte: Wikimedia Commons.

Modos normais em uma corda

As condições de fronteira na corda determinam como os comprimentos de onda e as frequências são. Se uma corda no comprimento l for fixada por suas duas extremidades, não poderá vibrar com nenhuma frequência, porque os pontos em que a corda é fixa já são nós.

Além disso, a separação entre nós adjacentes é λ/2, e entre o nó e a barriga é λ/4, dessa maneira apenas para certos comprimentos de onda são produzidos ondas estacionárias: aqueles em que um número inteiro de λ/2 interno é ajustado de o:

(λ/2) = L, com n = 1, 2, 3, 4 .. .

Portanto:

λ = 2l/n

Os harmônicos

Os diferentes valores tomados λ são chamados harmônicos. Assim temos:

-Primeiro harmônico: λ = 2l

-Segundo harmônico: λ = l

-Terceiro harmônico: λ = 2 l/3

-Sala harmônica: λ = l/2

E assim por diante.

Velocidade e frequência

Embora a onda estacionária pareça não se mover, a equação ainda é válida:

v = λ. F

Portanto:

v = (2l/n) . F

F = NV/2L

Agora, pode -se demonstrar que a velocidade com que uma onda se move em uma corda depende da tensão t na mesma e sua densidade linear de massa μ (massa por unidade de comprimento) como:

Portanto:

Pode atendê -lo: cargas mortas: características, cálculo, exemplos

Características de ondas estacionárias

-Quando as ondas estão estacionárias, a onda resultante não se espalha como seus componentes, que vão de um lugar para outro. Há pontos em que y = 0 porque não há vibração: os nós, em outras palavras, a amplitude para_R É zero.

-A expressão matemática de uma onda estacionária consiste no produto de uma parte espacial (que depende da coordenada X ou das coordenadas espaciais) e de uma parte temporal.

-Entre os nós, o onda preta resultante oscila em um só lugar, enquanto as ondas que passam de um lugar para outro estão desatualizadas lá.

-Apenas nos nós, a energia não é transportada, pois isso é proporcional ao quadrado da amplitude, mas está preso entre os nós.

-A distância entre nós adjacentes é metade do comprimento de onda.

-Os pontos em que a corda é fixa também são considerados nós.

Pessoal

Ondas estacionárias em uma dimensão

As ondas em uma corda fixa são exemplos de ondas estacionárias em uma dimensão, cuja descrição matemática que oferecemos nas seções anteriores.

Ondas estacionárias em duas e três dimensões

Ondas estacionárias também podem ser apresentadas em duas e três dimensões, sendo uma descrição matemática um pouco mais complexa.

Exemplos de corrida de Ondas

Cordas fixas

-Uma corda fixada por extrema que é oscilada à mão ou com um pistão por outro gera ondas estacionárias ao longo de seu comprimento.

Instrumentos musicais

Ondas estacionárias são criadas em instrumentos musicais, como Violoncello. Fonte: Pixabay.

-Ao tocar instrumentos de cordas como guitarra, harpa, violino e piano.

Ondas Stlover também são criadas em tubos de ar, como tubos de órgãos.

Edifícios e pontes

Ondas estacionárias surgem em estruturas como pontes e edifícios. Um caso notável foi o da ponte de suspensão de Tacoma estreita perto da cidade de Seattle, Estados Unidos. Logo após ser inaugurado em 1940, esta ponte caiu por causa das ondas estacionárias criadas dentro do vento.

A frequência do vento combinou com a frequência natural da ponte, criando em ondas estacionárias nisso, que estavam aumentando sua amplitude até que a ponte caiu. O fenômeno é conhecido como ressonância.

Pode servir a você: reflexão leve

Seiches

Nos portos, há um fenômeno muito curioso chamado Seiche, em que as ondas do mar produzem grandes oscilações. Isso ocorre porque as águas no porto estão bastante fechadas, embora as águas oceânicas penetrem de vez em quando através da entrada do porto.

Port Waters se move com sua própria frequência, bem como as do oceano. Se ambas as águas correspondem às suas frequências, há uma grande onda estacionária devido a ressonância, como aconteceu com a ponte Tacoma.

O Seiches Eles também podem ocorrer em lagos, reservatórios, piscinas e outros corpos de água limitados por superfícies.

Tanques de peixes

Ondas estacionárias podem ser criadas em um aquário transportado por uma pessoa, se a frequência com que a pessoa for igual à frequência do balanço da água.

Exercício resolvido

A corda de guitarra tem l = 0.9 me densidade de massa linear μ = 0.005 kg/m. É submetido a 72 N de tensão e seu modo de vibração é aquele que mostra a figura, com amplitude 2a = 0.5 cm.

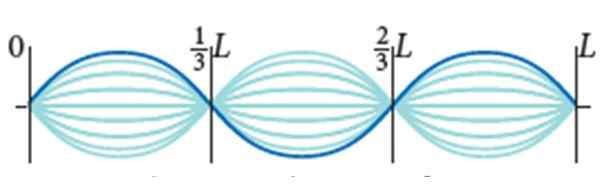Ondas estacionárias em uma corda de guitarra. Fonte: Bauer, W. Físico.

Encontrar:

a) velocidade de propagação

b) Frequência de onda

c) a equação de onda estacionária correspondente.

Solução para

Através:

Se obtem;

V = [72 n/(0.005 kg/m)]^1/2  = 120 m/s.

Solução b

A distância entre dois nós adjacentes é λ/2, portanto:

(2/3) L - (1/3) L = λ/2

(1/3) L = λ/2

λ = 2l/3 = 2 x 0.90 m / 3 = 0.60 m.

Como v = λ.F

F = (120 m/ s)/ 0.60 m = 200 s^-1= 200 Hz.

Solução c

A equação é:

e_R = [2a sen kx] . cos ωt

Precisamos substituir os valores:

K = 2π/ λ = k = 2π/ 0.60 m = 10 π/3

F = ω / 2π

Ω = 2π x 200 Hz = 400 π Hz.

A amplitude 2A já é dada pela declaração:

2a = 0.5 cm = 5 x 10 ^-3 m.

Portanto:

e_R = 5 x 10 ^-3 m . sin [(10π/3) x] . cos (400πt) =

= 0.5 cm . sin [(10π/3) x] . cos (400πt)

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill.
2. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 7. Ondas e física quântica. Editado por Douglas Figueroa (USB).
3. Giancoli, d.  2006. Física: Princípios com aplicações. 6º. Ed Prentice Hall.
4. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7º. Ed. Cengage Learning.
5. Tipler, p. (2006) Física para ciência e tecnologia. 5ª ed. Volume 1. Editorial revertido.
6. Wikipedia. Seiche. Recuperado de: é.Wikipedia.org.