Notação decimal
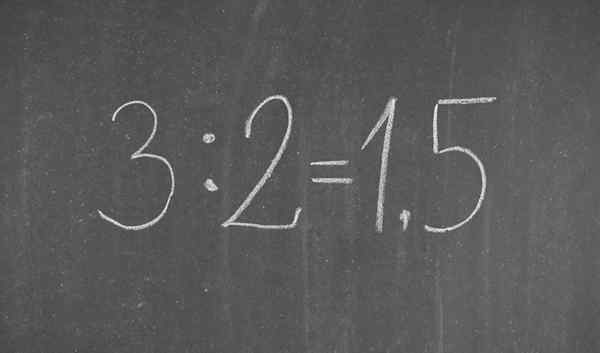
- 4670
- 80
- Pete Wuckert
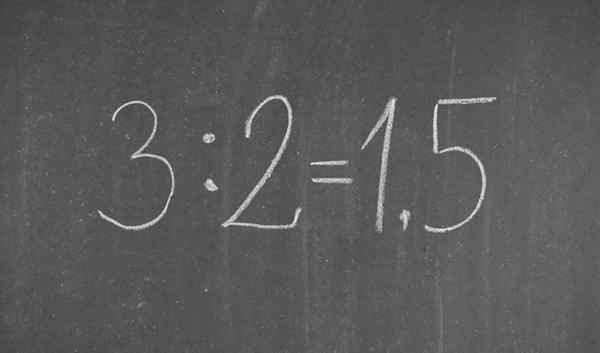 A fração 3/2 escrita em notação decimal
A fração 3/2 escrita em notação decimal O que é notação decimal?
O notação decimal Consiste em escrever um número real através de uma parte inteira e uma parte decimal, ambos separados por um ponto ou vírgula. A parte inteira é deixada e a parte decimal à direita desse ponto.
O 0 pode aparecer tanto em toda a parte quanto no decimal. Por exemplo, os números a seguir são números decimais:
- 0.25
- 1.5903
- 4.19367
Observe que a parte decimal desses números é finita, mas também há números com uma parte decimal infinita, como 0,33333 ..., onde pontos suspeitos são colocados como uma maneira de indicar que o número de decimais continua indefinidamente.
Em geral, um número decimal finito pode ser escrito como:
N.para1para2para3… paran
Sendo n um número inteiro e n a quantidade de decimais, enquanto um decimal infinito adota o formulário:
N.para1para2para3..
No decimal 0.25 são identificados:
- N = 0
- para1 = 2
- para2 = 5
Decimais surgem como outra maneira de expressar números racionais, que são aqueles que são moldados ou quebrados. De fato, qualquer fração pode ser escrita em notação decimal, como será visto imediatamente.
Eles também servem para representar números que não derivam de uma fração, o So -chamado números irracionais, como: π, √2, √3, √5, o número "e" e muitos outros.
Exemplos de números decimais
Um número decimal pode ser obtido de uma fração de uma maneira muito simples: calcular o quociente do numerador entre o denominador. Se o denominador for a unidade seguida por Zeros, isso é muito simples:
- 8/10 = 0.8
- - (5/100) = −0.05
No primeiro caso, como o denominador é 10, o ponto decimal é colocado imediatamente à esquerda do 8 e o decimal 0.8 diz "8 décimos" ou "ponto zero oito".
No segundo caso, como o denominador é de 100, você deve colocar o ponto decimal dois lugares à esquerda de 5 e, como o número é negativo, lê "menos 5 centésimos" ou "menos zero ponto cinco".
Quando o denominador não é a unidade seguida por 0, a divisão longa é usada:

Observe que, para realizar esta divisão, pois o numerador é menor que o denominador, foi multiplicado primeiro por 10 e, ao fazê -lo, um seguido pelo ponto decimal do quociente, para não alterar a operação, para que não Para alterar a operação. Em seguida, prossiga normalmente para dividir 10 por 2, que é igual a 5 e o resíduo de divisão é 0.
Pode atendê -lo: quantidades de vetorA forma decimal de fração ½ é 0.5, que "Zero Point Cinco" é lido:
Fração 7/8 é outro exemplo. Como 7 é menor que 8, ele multiplica 7 × 10 = 70, um 0 é colocado no quociente seguido pelo ponto decimal e é normalmente dividido:
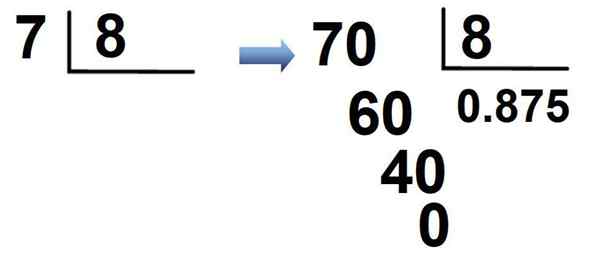
O resultado é que a fração é escrita em notação decimal como:
7/8 = 0.875
Esse número, como o resultado anterior, é um decimal finito e uma maneira de ler é: "Zero Point Oitocentos e setenta -cinco". Através deste procedimento, as seguintes frações também são escritas em notação decimal:
8/10 = 0.8
5/7 = 0.714285714…
9/20 = 0.Quatro cinco
3/8 = 0.375
Observe que, como em todas essas frações, o numerador é menor que o denominador, toda a parte das decimais resultantes é 0. No entanto, um número misto ou um Fração imprópria (Que cujo numerador é maior que seu denominador) também tem representação decimal.
Nesse caso, toda a parte é maior ou igual a 1 se a fração for positiva e menor que -1 se for negativa:
9/4 = 2.25
10/3 = 3.333333…
−12/5 = −2.4
1 ½ = 1.5
2 ¾ = 2.75
Parte inteira e parte fracionária das decimais negativos
Nos exemplos anteriores, observou -se que, para encontrar a expressão decimal de uma fração, um numerador e denominador são simplesmente divididos. Mesmo que a fração seja negativa, simplesmente o sinal menos é colocado na expressão decimiente equivalente.
No entanto, toda a parte e a parte fracionária de um decimal diferem de acordo com o sinal que você carrega.
Quando um decimal é positivo, como 2.25, sua parte inteira é 2 e sua parte decimal é 0.25 e o número pode ser escrito como a soma de toda a parte e a parte decimal, como esta:
2.25 = 2 + 0.25
Toda a parte é definida como o número inteiro imediatamente menor que o decimal e a parte decimal é sempre positiva. Para 2.25, o número inteiro imediatamente inferior é 2.
Mas no caso da fração -12/5, equivalente ao decimal -2.4 O acima não funciona.
Pode atendê -lo: quais são as partes do avião cartesiano?)
−2 + 0.4 = −1.6 ≠ −2.4
Portanto, toda a parte de -2.4 não pode ser -2, mas o número inteiro imediatamente inferior: -3. Mas nesse caso, a parte fracionária não seria 0.4, desde que adicionando:
−3 + 0.4 = −2.6 ≠ −2.4
Então, qual é a parte decimal do número negativo -2.4? Está subtraindo o número decimal de toda a sua parte e o resultado sempre será positivo:
−2.4 - ( - 3) = 0.6
Finalmente, está comprovado que, ao adicionar toda a parte e a parte fracionária, é obtido o decimal procurado:
−3 + 0.6 = −2.4
O procedimento para encontrar uma parte inteira e decimal de qualquer número, independentemente do sinal, é resumida dessa maneira:
- A parte inteira é o número inteiro imediatamente menor que o número decimal.
- A parte decimal é calculada subtraindo o decimal de toda a sua parte.
No entanto, para fins de cálculo prático, o número decimal -2.4 pode ser quebrado como - (2 + 0.4) = - 24/10 ou:
)
Tipos de decimais
Existem números decimais cuja parte decimal é finita ou infinita, que é usada como critério de classificação:
Decimais finitos ou exatos
Quando os decimais são finitos, como 0.125, também é dito que eles são decimais exatos.
Decimais infinitos
Um decimal infinito é obtido quando o resíduo da divisão entre numerador e denominador nunca é feito 0.
Desde que o decimal venha do quociente entre dois números inteiros, essa parte decimal é periódica, ou seja, é composta por uma ou várias figuras que são repetidas indefinidamente, chamadas período.
Por exemplo, número 3.3333333… originado pela fração inadequada 10/3, é um decimal periódico: toda a parte é 3 e, após o ponto decimal, o número 3 é repetido indefinidamente. Isso pode ser simbolizado colocando uma curva ou chapéu no número que é repetido:



Finalmente, existem decimais infinitos que não são jornais, que não se originam do quociente entre dois números inteiros. Como mencionado no início, esses decimais pertencem a todo números irracionais, Como o número PI, por exemplo.
Exercícios resolvidos
Exercício 1
Escreva numéricos os seguintes números decimais:
a) Ponto zero quatrocentos quarenta -sete
b) Cinco milésimos
c) duas unidades e quinhentos centésimos
d) três pontos vinte e sete negativos
e) um ponto oitocentos e mil e mil e quinhentos sessenta e três
-
Solução
a) 0.447
b) 0.005
c) 2.05
d) −3.27
e) 1.824563
Exercício 2
Classifique os seguintes números decimais em jornais decimais e puros, jornais mistos ou números irracionais. Em todos os casos, indique o valor de toda a parte e, se forem jornais ou jornais mistos, também indicam o valor do período e do anterior, conforme apropriado:
a) 0.35627
b) 1.21212121…
c) -1.32
d) 1.414213562… = √2
-
Solução
a) 35627 é um decimal exato. Toda a sua parte é 0 e sua parte decimal é 0.35627.
b) 1.21212121… é um jornal decimal e puro infinito, toda a parte é 1 e o período é 21.
c) -1.32 é um decimal exato e negativo, cuja parte inteira é -2. A parte decimal é calculada subtraindo o número decimal de toda a parte:
-1.32 - (−2) = 0.68
d) A expressão decimal de √2 é infinita e não periódica, pois é um número irracional.
É um jornal misto, toda a parte é 3, o anterior é 1 e o período é 89.
Referências
- Contribuições pedagógicas e material didático. Notação decimal. Recuperado de: Tecdigital.Tec.AC.Cr.
- Baldor, a. 2007. Aritmética teórica prática. Grupo Editorial Patria S.PARA. claro.V.
- Matemática para negociações. Compreensão da notação decimal. Recuperado de: OpenTextBC.AC.
- Unam. Números racionais: significados e representações. Recuperado de: Redi.Codeic.Unam.mx.



&space;\:&space;3.1\widehat89)