Números ímpares

O que são números estranhos?

O números ímpares Eles são aqueles números inteiros que não são divisíveis por 2. Isso significa que, com quantidades estranhas, você não pode fazer grupos de 2, por exemplo, se alguém tiver 9 doces para compartilhar com um amigo e não quiser dividir nenhum, eles tocarão 4 doces e os outros 5.

Alguns dos números ímpares são os seguintes: ... -5, -3, -1, 1, 3, 5, 7, 9, 11, 13 ..  Nesta expressão, os pontos suspeitos indicam que há mais números, à esquerda e à direita.

Figura 1: Como saber se um número é estranho?

Olhando cuidadosamente, você pode ver que cada número ímpar pode ser obtido adicionando 2 ao número anterior. Por exemplo, se adicionarmos 2 a -1, você receberá 1, se fizermos 1 + 2, é 3 e assim por diante.

Observa -se também que, se os pares forem intercalados, incluindo 0, o que é considerado um número par, o conjunto de números inteiros é obtido Z.

É por isso que qualquer número natural ímpar pode ser escrito no formulário 2n + 1, onde n = 0, ± 1, ± 2, ± 3, ± 4, ± 5…, onde o símbolo ± significa que pode ser considerado positivo ou como negativo.

No caso de números maiores, pode ser reconhecido quando é estranho, porque sempre termina em 1, 3, 5, 7 ou 9. Por exemplo, 1571 é estranho e o número inteiro negativo -152 também.489.

Exemplos de números estranhos

Os números ímpares são frequentemente apresentados na natureza, e entre eles o número 3 é de especial significância. Vejamos alguns exemplos:

-Existem muitas flores com um número estranho de pétalas.

-Temos 5 dedos em cada mão.

Pode servir a você: variável aleatória: conceito, tipos, exemplos

-Os seres humanos têm 23 pares de cromossomos.

-Existem 3 leis de Newton e as 3 leis da termodinâmica.

-Os núcleos dos átomos que têm um número ímpar de prótons e nêutrons são menos estáveis ​​do que aqueles com um número de pares.

-Os magos são 3.

-Em histórias e histórias, o número 3 aparece freqüentemente, por exemplo, romances como Os três Mosqueteiros por Alejandro Dumas e em histórias populares como Os três irmãos e Os três Porquinhos.

-Para a composição artística, existe a chamada Regra estranha, que estabelece que uma composição com um número ímpar de elementos é mais atraente do que um com um casal. O número ímpar adiciona dinamismo, enquanto um par fornece estabilidade.

Figura 2. Um número ímpar de elementos adiciona dinamismo a uma imagem

-Uma estratégia comum para fazer com que os preços dos objetos pareçam mais baratos é terminar 9, por exemplo 2.US $ 99, US $ 39 e assim por diante.

-O número 13 é considerado má sorte por alguns, enquanto outros atribuem qualidades místicas a 11, ambos os números ímpares.

Números primos

Números primos, aqueles que só admitem como divisores e 1, são estranhos, com exceção de 2, que é o único primo Torque.

É possível demonstrar que qualquer número pode ser dividido como um produto de fatores primos (incluindo esses poderes) e que essa maneira de expressar o número é única, exceto na ordem dos fatores.

Por exemplo, o número 45 pode ser quebrado como 45 = 3³ x 5.

Operações de números ímpares

Com os números ímpares, todas as operações aritméticas são realizadas e algumas têm características excelentes.

Pode atendê -lo: simbolização de expressões

- Somas e produtos

-A soma de dois números ímpares resulta em um número par: 3+5 = 8; 11+15 = 26; (-10)+ (+6) = - 4.

-Ao adicionar um número ímpar com um torque, o resultado é ímpar: 7+2 = 9; 26+ 9 = 35; (-5) + 12 = 7.

-Se o n Primeiro números naturais, estranhos e consecutivos, o resultado é n². Vamos ver isso com um pouco mais de detalhes:

Para n = 2: 1 + 3 = 4 = 2²

Para n = 3: 1 + 3 + 5 = 9 = 3²

Para n = 4: 1 + 3 + 5 + 7 = 16 = 4²

-Quando um ímpar é multiplicado por um par, um número par se origina: 7 x 4 = 28; (-3) x 12 = -36.

-Multiplicando dois números ímpares também é obtido: 3 x 5 = 15; (-5) x (+11) = -55.

- Poderes

-Quando um número positivo é aumentado para um poder estranho, é um número positivo, por exemplo: 3³ = 27.

-Ao aumentar um número negativo para um poder estranho, o resultado é negativo: (-2)³= (-2) x (-2) x (-2) = -8.

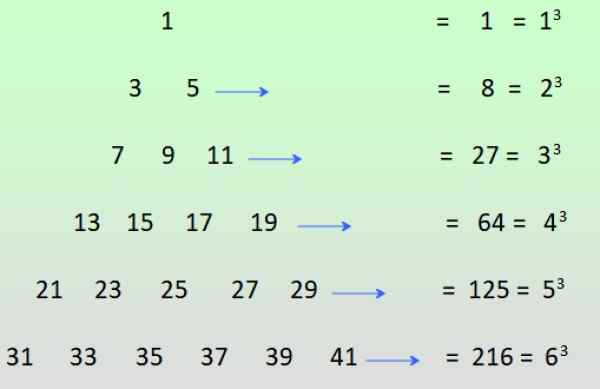
-Poderes ímpares de números inteiros positivos podem ser alcançados se números ímpares estiverem disponíveis como mostrado na figura e as linhas forem adicionadas:

Figura 3. Obtendo os poderes estranhos da soma de números ímpares. Fonte: f. Zapata.

Exercícios resolvidos

- Exercício 1

Decida se o resultado da operação a seguir é par ou ímpar:

(53476890083 + 1987628967) x 13567903

Solução

Para obter a resposta, você não precisa correr para procurar uma calculadora, mas para aplicar as propriedades vistas. Vejamos os últimos dígitos dos Administração, que são 3 e 7, respectivamente:

53476890083  + 1987628967

Isso significa que os viciados são estranhos e já sabemos que a soma de dois números ímpares é uniforme.

Portanto, a figura que resulta dos parênteses é uniforme e multiplicaremos por um número que termina em 3:

Pode servir você: álgebra vetorial

13567903

O que significa que esse número é estranho.

Nas propriedades descritas acima, foi estabelecido que multiplicar o torque x é um número par. Portanto, a operação resultante é uniforme.

- Exercício 2

Quanto é a soma dos 5 primeiros números ímpares consecutivos? E o dos primeiros 50?

Solução

A soma dos 5 primeiros números ímpares consecutivos é:

1 + 3 + 5 + 7 + 9 = 25

Mas se queremos adicionar os primeiros 50 dessa maneira, é pesado, então estamos indo para as propriedades. Eles afirmam que a soma de números ímpares consecutivos é n². Nesse caso, n = 50 e a soma solicitada é:

cinquenta² = 50 x 50 = 2500.

- Exercício 3

Quando três números ímpares consecutivos são adicionados, 237 são obtidos. Quais são os números?

Solução

Vamos chamar nosso primeiro número ímpar, e o segundo e Z para o terceiro, de acordo com a declaração, é cumprido que:

x + y + z = 237

Na linguagem algébrica, qualquer número ímpar pode ser escrito no formulário 2n +1. Vamos fazer nosso primeiro número ímpar:

x = 2n +1

Vamos adicionar 2 para obter o seguinte ímpar:

y = x + 2 = (2n + 1) + 2 = 2n + 3

E finalmente é adicionado novamente 2 para obter o terceiro ímpar:

Z = (2n +3) + 2 = 2n + 5

Tudo isso acrescenta:

2n + 1 + 2n + 3 + 2n + 5 = 237

6n + 9 = 237

Isso resulta em uma equação linear simples, cuja solução é:

n = 38

E agora com o valor de n = 38, existem os três pedidos:

x = (2 × 38) + 1 = 77

A seguir, são ímpares consecutivas, portanto:

y = 79

Z = 81

E o leitor pode verificar facilmente se a soma dos três é 237.

Referências

1. Baldor, a. 1986. Aritmética. Edições e distribuições Codex.
2. Bairros, l. Os números ímpares e os poderes de números naturais. Recuperado de: Sinewton.org.
3. Brilhante. Números pares e estranhos. Recuperado de: brilhante.org.
4. Matemática 18. Operações de números ímpares. Recuperado de: Matemática18.com.
5. Wikipedia. Números pares e estranhos. Recuperado de: é.Wikipedia.org.