Exercícios e exercícios de ângulos alternativos externos resolvidos resolvidos

O ângulos alternativos externos São os ângulos que são formados quando duas linhas paralelas são interceptadas com uma linha de secagem. Além desses ângulos, outro torque é formado que são chamados de ângulos alternativos internos.

A diferença entre esses dois conceitos são as palavras "externas" e "internas" e, como é o nome indicado, os ângulos alternativos externos são aqueles que são formados fora das duas linhas paralelas.

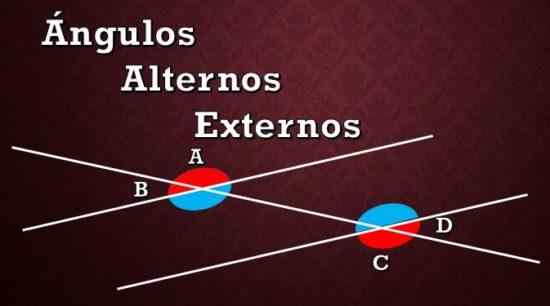
Representação gráfica de ângulos externos alternativos A, B e C, D

Como pode ser visto na imagem anterior, existem oito ângulos formados entre as duas linhas paralelas e a linha de secagem. Os ângulos vermelhos são os alternados externos e os ângulos azuis são os ângulos alternativos internos.

[TOC]

Características de ângulos alternativos externos

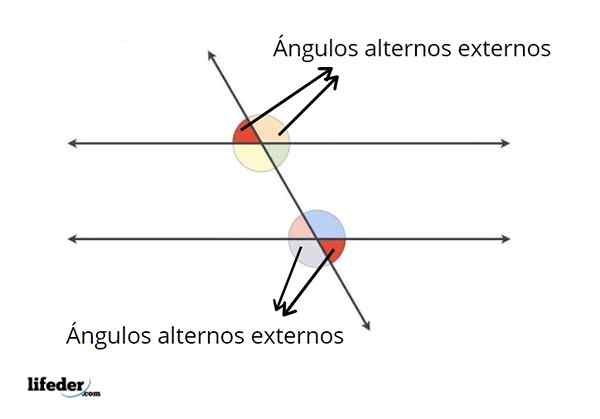Exemplos de ângulos alternativos externos

Na introdução, já foi explicado quais são os ângulos alternativos externos. Além de serem os ângulos externos entre os paralelos, esses ângulos atendem a outra condição.

A condição que eles conhecem é que os ângulos alternativos externos formados em uma linha paralela são congruentes; Tem a mesma medida que os outros dois que são formados na outra linha paralela.

Mas cada ângulo alternativo externo é congruente com um do outro lado da linha secante.

Quais são os ângulos alternativos externos congruentes?

Se a imagem do início e a explicação anterior for observada, pode -se concluir que os ângulos alternativos externos que são congruentes entre si são: ângulos A e C e ângulos B e D.

Para demonstrar que eles são congruentes.

Pode atendê -lo: função constante: características, exemplos, exercícios

Exercícios resolvidos

Abaixo estão uma série de exercícios onde a definição e a propriedade da congruência dos ângulos alternativos externos devem ser aplicados.

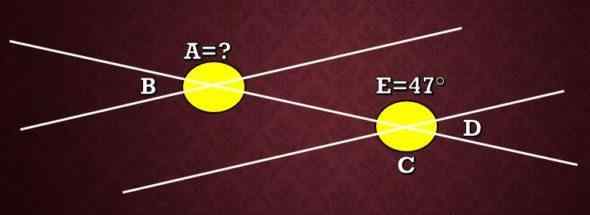
Primeiro exercício

Na imagem a seguir, qual é a medida do ângulo e sabendo que o ângulo E mede 47 °?

Solução

Como explicado anteriormente, os ângulos A e C são congruentes por serem alternados externos. Portanto, a medida de A é igual à medida de C. Agora, como os ângulos E e C são ângulos opostos pelo vértice, eles têm que têm a mesma medida, portanto, a medida de C é 47 °.

Em conclusão, a medida é igual a 47 °.

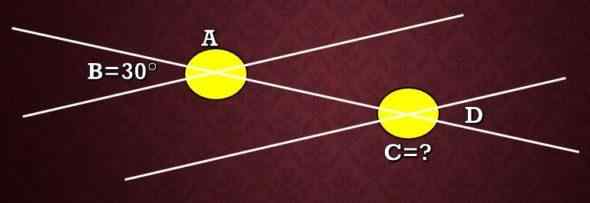
Segundo exercício

Calcule a medida do ângulo C mostrado na imagem a seguir, sabendo que o ângulo B mede 30 °.

Solução

Neste exemplo, a definição é usada. Dois ângulos são suplementares se a soma de suas medidas for igual a 180 °.

Na imagem, pode -se observar que A e B são suplementares, portanto A+B = 180 °, isto é, a+30 ° = 180 ° e, portanto, a = 150 °. Agora, como A e C, são ângulos alternativos externos, então suas medidas são iguais. Portanto, a medida C é de 150 °.

Terceiro exercício

Na imagem a seguir, a medida do ângulo A é de 145 °. Qual é a medida do ângulo e?

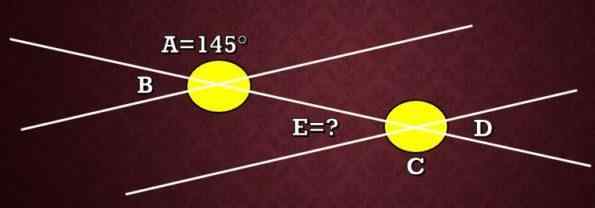
Solução

Na imagem, pode -se observar que os ângulos A e C são ângulos alternativos externos, portanto, eles têm a mesma medida. Ou seja, a medida de C é 145 °.

Como os ângulos C e E são ângulos suplementares, deve ser C+E = 180 °, ou seja, 145 °+E = 180 ° e, portanto, a medida do ângulo E é 35 °.

Pode servir a você: Erro de amostragem: fórmulas e equações, cálculo, exemplos

Referências

1. Bourke. (2007). Um ângulo na pasta de trabalho de matemática da geometria. Aprendizagem de NewPath.
2. C. E. PARA. (2003). Elementos de geometria: com numerosos exercícios e geometria da bússola. Universidade de Medellin.
3. Clemens, s. R., O'DAFER, p. G., & Cooney, T. J. (1998). Geometria. Pearson Education.
4. Lang, s., & Murrow, G. (1988). Geometria: um curso do ensino médio. Springer Science & Business Media.
5. Lira, a., Jaime, p., Chávez, m., Gallegos, m., & Rodríguez, C. (2006). Geometria e trigonometria. Edições de Umbral.
6. Moyano, a. R., Saro, a. R., & Ruiz, r. M. (2007). Álgebra e geometria quadrática. Netbiblo.
7. Palmer, c. Yo., & Bibb, S. F. (1979). Matemática Prática: Aritmética, Álgebra, Geometria, Trigonometria e Regra de Cálculo. Reverte.
8. Sullivan, m. (1997). Trigonometria e geometria analítica. Pearson Education.
9. Wingard-Enelson, r. (2012). Geometria. Enslow Publishers, Inc.