Ângulo registrado de uma definição de círculo, teoremas, exemplos

Ele ângulo registrado de um círculo É o que tem seu vértice na circunferência e sua semi -estima é seca ou tangente à mesma. Como conseqüência, o ângulo registrado sempre será convexo ou plano.

Na Figura 1, vários ângulos registrados em suas respectivos circunferências são representados. O ângulo ero é registrado por ter seu vértice na circunferência e seus dois semi -recrengers [de) e [df) secando a circunferência. 

figura 1. Vários ângulos inscritos sobre suas respectivas circunferências. Fonte: f. Zapata com geogebra.

Da mesma forma, o ângulo portehgi está registrado, por ter seu vértice na circunferência e seus lados secos para o mesmo.

Os ângulos portekjr e porte também estão registrados com a circunferência. O primeiro tem um lado secante e o outro tangente, enquanto o segundo tem seus dois lados tangentes à circunferência, formando um ângulo plano de plano (180º).

Alguns autores chamam um ângulo semi-inscrito para quem tem um de seus lados tangente à circunferência, mas neste artigo ele é considerado registrado.

Qualquer ângulo registrado define ou subtende um arco associado ao mesmo. Por exemplo, na Figura 2, o ângulo registrado ero subtende o arco a⌒c de comprimento d.

A mesma figura mostra o ângulo porte, que não está registrado na circunferência por não ter seu vértice em sua circunferência, mas no centro ou.

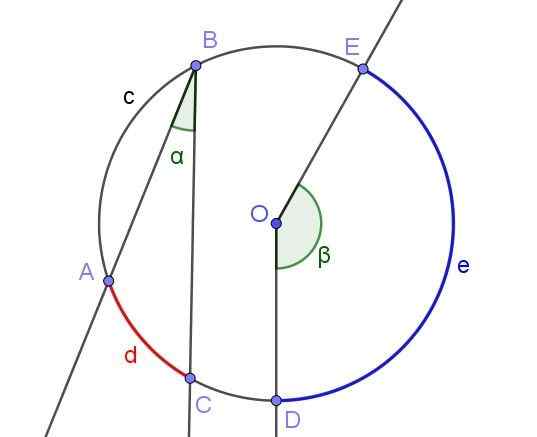Figura 2. Ângulo registrado porte e ângulo central porte. Fonte: f. Zapata com geogebra.

[TOC]

Ângulo central

Além do ângulo registrado, o ângulo central, qual é aquele cujo vértice está no centro da circunferência e cujos lados cortam a circunferência.

Pode atendê -lo: diferença entre uma fração comum e um número decimal

A medida de Radianes de um ângulo central é o quociente entre o arco que subtende, ou seja, o arco de circunferência entre os lados do ângulo e o raio da circunferência.

Se a circunferência for unitária (raio 1), o comprimento do arco nas mesmas unidades de rádio é a medida do ângulo em Radianes.

E quando a medida do ângulo é necessária em graus, a medida é multiplicada em radianos pelo fator 180º/π.

Os instrumentos de medição de ângulos sempre usam um ângulo central e o comprimento do arco subtendido por isso diretamente calibrado em graus. Isso significa que sempre que um ângulo é medido, no fundo o que é medido é o comprimento do arco subtendido pelo ângulo central.

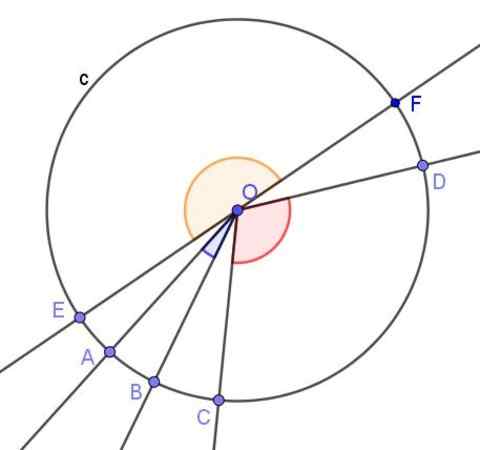Figura 3. Vários ângulos centrais da circunferência. Fonte: f. Zapata com geogebra.

Teoremas

- Teorema 1 (ângulo registrado e ângulo central)

A medida de um ângulo registrado é metade da medida do ângulo central, se ambos os ângulos subtite o mesmo arco.

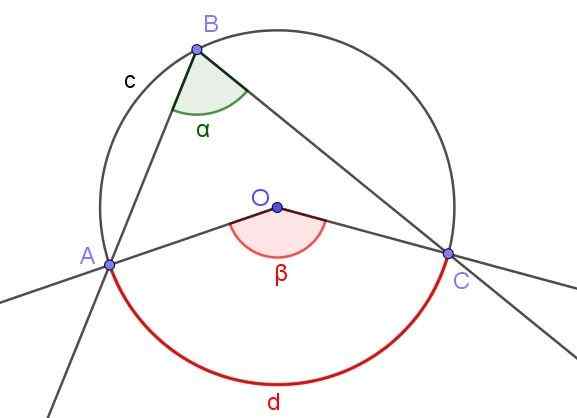Figura 4. Ângulo registrado porte e ângulo central porte que subtita o mesmo arco a⌒c. Fonte: f. Zapata com geogebra.

A Figura 4 mostra dois ângulos porte e porte, que cruzam o mesmo arco de circunferência A⌒C.

Se a medida do ângulo registrado for α, a medida β do ângulo central é o dobro da medida do ângulo registrado (β = 2 α) porque ambos subtraem o mesmo arco medido d D.

Demonstração 1

Para demonstrar o teorema 1, vários casos específicos começarão, até chegar ao caso geral.

Pode atendê -lo: Lei de Sanduíche: Explicação e Exercícios

Suponha que um ângulo registrado, no qual um de seus lados passa pelo centro da circunferência, como mostrado na Figura 5.

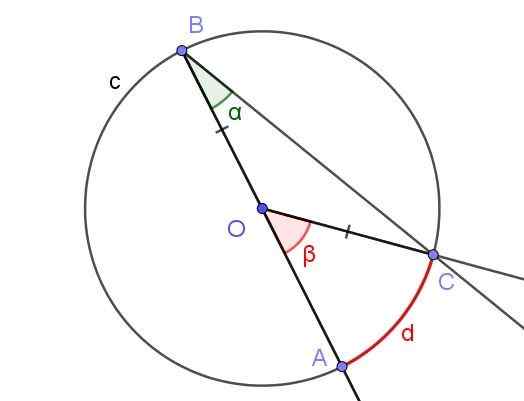Figura 5. Ângulo registrado porte com o lado [BA) através do ângulo O e Central porte. Fonte: f. Zapata com geogebra.

Nesse caso, é formado o Triange de Isoceles de espuma, já que [oc] = [ob].

Em um triângulo de isósceles, os ângulos adjacentes à base são os mesmos, portanto, eles precisam portebCo = eroBC = α. Por outro lado, ϩcob = 180º - β.

Considerando a soma dos ângulos internos do triângulo Cob que você tem:

α + α + (180º - β) = 180º

Onde se segue que 2 α = β, ou o que é equivalente: α = β/2. Isso coincide com o que o Teorema 1 afirma: A medida do ângulo registrado é metade do ângulo central, se ambos os ângulos enviarem a mesma corda [AC].

Demonstração 1b

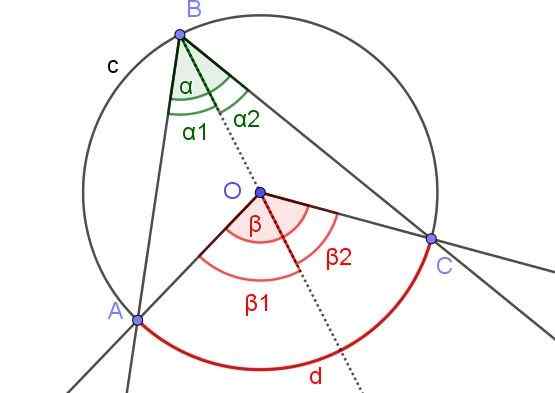Figura 6. Construção auxiliar para demonstrar que α = β/2. Fonte: f. Zapata com geogebra.

Nesse caso, existe um ângulo inscrito ero, no qual o centro ou a circunferência está dentro do ângulo.

Para demonstrar o teorema 1 neste caso, o semi -Auxiliar [BO) é desenhado, de modo que existem dois ângulos registrados porte e ero porte adjacente ao referido semi -recreação.

Da mesma forma, eles têm os ângulos centrais β₁ e β₂ adjacente ao referido semi -recreação. Dessa forma, você tem a mesma situação que na demonstração 1, para que possa ser afirmado que α₂ = β₂ /2 e α₁ = β₁ /2. Como α = α₁ + α₂ e β = β₁ + β₂ Existe, portanto, que α = α₁ + α₂ = β₁ /2 + β₂ /2 = (β₁ + β₂) / 2 = β / 2.

Pode atendê -lo: tipos de integrais

Em conclusão α = β / 2, que encontra o teorema 1.

- Teorema 2

Se dois ou mais ângulos registrados subtesem o mesmo arco, eles têm a mesma medida.

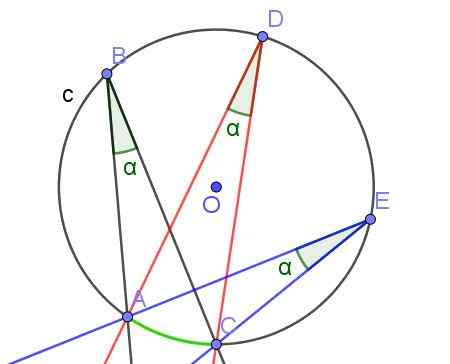Figura 7. Ângulos registrados de igual medida α, porque eles subtem o mesmo arco a⌒c. Fonte: f. Zapata com geogebra.

- Teorema 3

Os ângulos registrados subtit. Existem sequências da mesma medida.

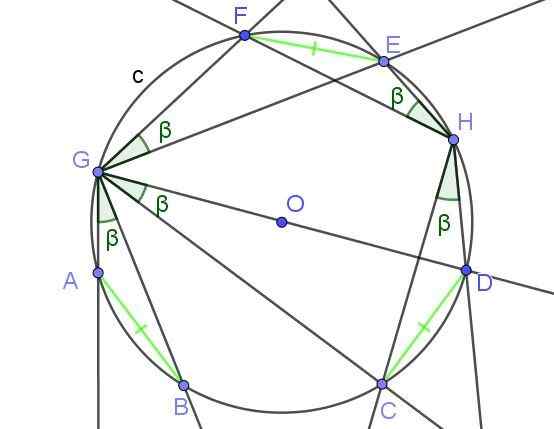Figura 8. Os ângulos inscritos que subtuse as cordas de igual medida têm igual medida β. Fonte: f. Zapata com geogebra.

Exemplos

- Exemplo 1

Demonstrar que o ângulo inscrito subtita o diâmetro é um ângulo certo.

Solução

O ângulo central porte associado ao diâmetro é um ângulo plano, cuja medida é 180º.

De acordo com o Teorema 1, qualquer ângulo registrado na circunferência que subtende a mesma corda (neste caso o diâmetro), tem como medida a metade do ângulo central que subtita a mesma corda, que para o nosso exemplo é 180º/2 = 90º.

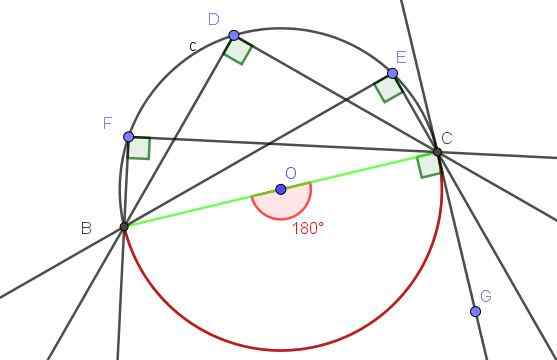Figura 9. Qualquer ângulo registrado que subtende ao diâmetro é um ângulo reto. Fonte: f. Zapata com geogebra.

- Exemplo 2

A linha (BC) tangente em A A a a circunferência C, determina o ângulo inscrito ero (veja a Figura 10).

Verifique se o teorema 1 dos ângulos registrados é cumprido.

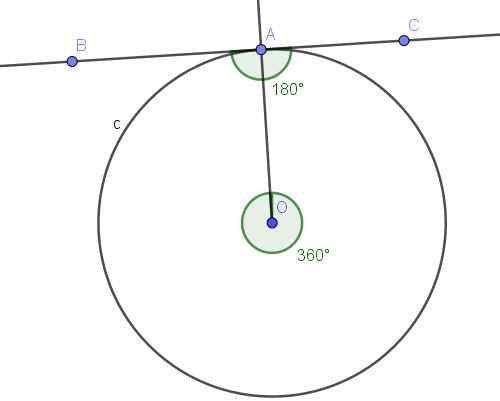Figura 10. Ângulo registrado BAC e seu ângulo central convexo AoA. Fonte: f. Zapata com geogebra.

Solução

O ângulo portebac é registrado porque seu vértice está na circunferência, e seus lados [ab) e [ac) são tangentes à circunferência, portanto a definição de ângulo inscrito é atendido.

Por outro. O ângulo central que subtende o arco A⌒a é um ângulo convexo cuja medida é o ângulo total (360º).

O ângulo registrado subtita o arco completo mede metade do ângulo central associado, isto é, portebac = 360º/2 = 180º.

Com tudo o que acima está provado que este caso em particular atende ao teorema 1.

Referências

1. Baldor. (1973). Geometria e trigonometria. Editorial cultural da América Central.
2. E. PARA. (2003). Elementos de geometria: com exercícios e geometria da bússola. Universidade de Medellin.
3. Geometria 1ª. Ângulos na circunferência. Recuperado de: edu.Xunta.é/
4. Toda ciência. Exercícios propostos de ângulos na circunferência. Recuperado de: Francesphysics.Blogspot.com
5. Wikipedia. Ângulo registrado. Recuperado de: é.Wikipedia.com