Metodologia de amostragem aleatória, vantagens, desvantagens, exemplos

Ele amostragem aleatória É a maneira de selecionar uma amostra estatisticamente representativa de uma determinada população. Parte do princípio de que todo elemento da amostra deve ter a mesma probabilidade de ser selecionado.

Um sorteio é um exemplo de amostragem aleatória, na qual cada membro da população de participantes recebe um número. Para escolher os números correspondentes ao Raffle Awards (a amostra), alguma técnica aleatória é usada, por exemplo, extrato de uma caixa de correio os números que foram pontuados em cartões idênticos.

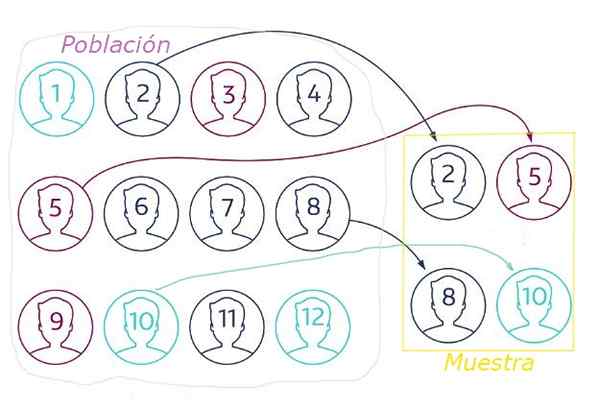figura 1. Na amostragem aleatória, a amostra é extraída da população aleatória através de alguma técnica que garante que todos os elementos tenham a mesma probabilidade de ser escolhido. Fonte: NetQuest.com.

Na amostragem aleatória, é essencial.

[TOC]

O tamanho da amostra

Existem fórmulas para determinar o tamanho adequado de uma amostra. O fator mais importante a considerar é se o tamanho da população é ou não conhecido. Vejamos as fórmulas para determinar o tamanho da amostra:

Caso 1: O tamanho da população não é conhecido

Quando o tamanho da população é desconhecido, é possível selecionar uma amostra adequada de n, para determinar se uma certa hipótese é verdadeira ou falsa.

Para isso, é usada a seguinte fórmula:

n = (z² P q)/(e²)

Onde:

-P É a probabilidade de que a hipótese seja verdadeira.

-Q é a probabilidade de que não seja, portanto q = 1 - p.

-E é a margem relativa de erro, por exemplo, um erro de 5% tem uma margem e = 0,05. 

-Z tem a ver com o nível de confiança exigido pelo estudo.

Pode servir a você: distribuição normal: fórmula, características, exemplo, exercício

Em uma distribuição normal tipificada (ou normalizada), um nível de confiança de 90% tem z = 1.645, porque a probabilidade de o resultado estar entre -1.645σ e +1.645σ é 90%, onde σ é o desvio padrão.

Níveis de confiança e seus valores z correspondentes 

1.- O nível de confiança de 50% corresponde a z = 0,675.

2.- 68.O nível de confiança de 3% corresponde a z = 1.

3.- Nível de confiança de 90% equivalente a z = 1.645.

4.- O nível de confiança de 95% corresponde a z = 1,96

5.- 95,5% de nível de confiança corresponde a z = 2.

6.- 99,7% de confiança é equivalente a z = 3.

Um exemplo em que essa fórmula pode ser aplicada seria em um estudo para determinar o peso médio das seixos de uma praia.

Claramente não é possível estudar e pesar todas as seixos da praia, então é conveniente.

Figura 2. Para estudar as características dos seixos de uma praia, é necessário escolher uma amostra aleatória com um número representativo deles. (Fonte: Pixabay)

Caso 2: O tamanho da população é conhecido

Quando o número n de elementos que compõem uma determinada população (ou universo) é conhecida, se você deseja selecionar por amostragem aleatória simples de uma amostra estatisticamente significativa, esta é a fórmula: 

n = (z²p q n)/(n e² + Z²P Q)

Onde:

-Z é o coeficiente associado ao nível de confiança.

-P é a probabilidade de sucesso da hipótese.

-Q é a probabilidade de falha na hipótese, p + q = 1.

-N é o tamanho da população total.

-E é o erro relativo do resultado do estudo.

Exemplos

A metodologia para extrair as amostras depende muito do tipo de estudo necessário para fazer. Portanto, a amostragem aleatória possui inúmeras aplicações:

Pode atendê -lo: sinais de agrupamento

Pesquisas e questionários

Por exemplo, em pesquisas telefônicas, as pessoas são escolhidas para serem consultadas por um gerador de números aleatórios, aplicável à região em estudo.

Se você deseja aplicar um questionário aos funcionários de uma grande empresa, a seleção de entrevistados pode ser usada através do número do funcionário ou número do cartão de identidade.

Este número também deve ser escolhido aleatoriamente, usando um gerador de números aleatórios, por exemplo.

Figura 3. Um questionário pode ser aplicado selecionando aleatoriamente os participantes. Fonte: Pixabay.

Controle de qualidade

No caso de o estudo estar nas peças fabricadas por uma máquina, as peças devem ser escolhidas aleatoriamente, mas de lotes feitos em diferentes momentos do dia, ou em diferentes dias ou semanas.

Vantagens

Amostragem aleatória simples:

- Permite reduzir os custos de um estudo estatístico, porque não é necessário estudar a população total para obter resultados estatisticamente confiáveis, com os níveis de confiança desejados e o nível de erro exigido no estudo.

- Evite viés: Como a escolha dos elementos a serem estudados é completamente aleatoriamente, o estudo reflete fielmente as características da população, embora apenas parte do mesmo tenha sido estudada.

Desvantagens

- O método não é adequado nos casos em que você deseja conhecer as preferências em diferentes grupos ou estratos populacionais.

Nesse caso, é preferível determinar anteriormente os grupos ou segmentos nos quais o estudo é feito. Depois que os estratos ou grupos forem definidos, se for conveniente para cada um deles aplicar amostragem aleatória.

- É muito improvável que as informações sobre os setores minoritários sejam obtidos, dos quais às vezes é necessário conhecer suas características.

Pode atendê -lo: Simpson Regra: Fórmula, Demonstração, Exemplos, Exercícios

Por exemplo, se for uma campanha em um produto caro, é necessário conhecer as preferências dos setores minoritários mais ricos.

Exercício resolvido

Queremos estudar a preferência da população pela maneira como a cola da cola, mas não há estudo anterior nessa população, da qual seu tamanho é desconhecido.

Por outro lado, a amostra deve ser representativa com um nível mínimo de confiança de 90% e as conclusões devem ter um erro percentual de 2%.

-Como determinar o tamanho S da amostra?

-Qual seria o tamanho da amostra se a margem de erro for feita até 5%?

Solução

Como o tamanho da população é desconhecido, para determinar o tamanho da amostra, a fórmula dada acima é usada:

n = (z²P q)/(e²)

Assumimos que existe a mesma probabilidade de preferência (p) por nosso refresco a da não -preferência (q), então p = q = 0.5.

Por outro lado, como o resultado do estudo deve ter um erro percentual inferior a 2%, o erro relativo será 0,02.

Finalmente, um valor z = 1.645 produz um nível de confiança de 90%.

Em suma, você tem os seguintes valores:

Z = 1.645

P = 0,5

Q = 0,5

E = 0,02

Com esses dados, o tamanho mínimo da amostra é calculado:

N = (1.645² 0,5 0,5)/(0,02²) = 1691.3

Isso significa que o estudo com a margem de erro necessária e com o nível de confiança escolhido deve ter uma amostra de entrevistados de pelo menos 1692 indivíduos, escolhidos por amostragem aleatória simples.

Se você passar de uma margem de erro de 2% a 5%, o novo tamanho da amostra é:

N = (1.645² 0,5 0,5)/(0,05²) = 271

Que é um número significativamente menor de indivíduos. Em conclusão, o tamanho da amostra é muito sensível à margem desejada no estudo.

Referências

1. Berenson, m. 1985.Estatísticas para administração e economia, conceitos e aplicações. Editorial inter -americano.
2. Estatisticas. Amostragem aleatória. Retirado de: Encyclopediaeconomica.com.
3. Estatisticas. Amostragem. Recuperado de: estatísticas.Esteira.USON.mx.
4. Explorável. Amostragem aleatória. Recuperado de: explorável.com.
5. Moore, d. 2005. Estatísticas básicas aplicadas. 2º. Edição.
6. NetQuest. Amostragem aleatória. Recuperado de: netQuest.com.
7. Wikipedia. Amostra estatística. Recuperado de: em.Wikipedia.org