Método Gauss-Seidel Explicação, Aplicações, Exemplos

Ele Método Gauss-Seidel É um procedimento iterativo encontrar soluções aproximadas para um sistema de equações algébricas lineares com precisão arbitrariamente escolhida. O método se aplica a matrizes quadradas com elementos não -nula em suas diagonais e a convergência é garantida se a matriz for diagonalmente dominante.

Foi criado por Carl Friedrich Gauss (1777-1855), que fez uma demonstração privada a um de seus alunos em 1823. Posteriormente, foi formalmente publicado por Philipp Ludwig von Seidel (1821-1896) em 1874, daí o nome de ambos os matemáticos.

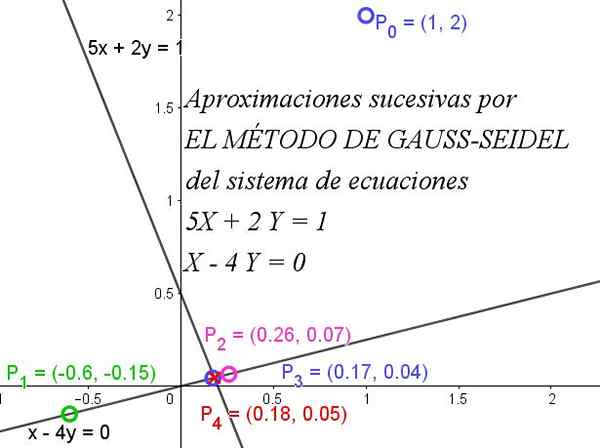
figura 1. O método de Gauss-Seidel converge rapidamente para obter um sistema de equações. Fonte: f. Zapata.

Para uma compreensão completa do método, é necessário saber que uma matriz é diagonalmente dominante quando o valor absoluto do elemento diagonal de cada linha é maior ou igual à soma dos valores absolutos dos outros elementos da mesma linha.

Matematicamente, é expresso da seguinte maneira:

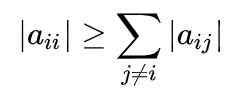
[TOC]

Explicação através de um caso simples

Para ilustrar o que o método Gauss-Seidel levará um caso simples, no qual você pode encontrar os valores de x e y no sistema de equações lineares 2 × 2 mostrado abaixo:

5x + 2y = 1

X - 4y = 0

Passos a seguir

1- Primeiro de tudo, você precisa determinar se a convergência está segura. Observa -se imediatamente que, na verdade, é um sistema diagonalmente dominante, pois na primeira linha o primeiro coeficiente tem um valor absoluto maior que os outros da primeira fila:

| 5 |> | 2 |

Da mesma forma, o segundo coeficiente da segunda linha também é diagonalmente dominante:

| -4 |> | 1 |

2- As variáveis ​​x e y são claras: 

X = (1 - 2y)/5

Y = x/4

3- Um valor arbitrário inicial é colocado, chamado "semente": xo = 1, eu = 2.

4

Pode atendê -lo: estimativa por intervalos

X1 = (1 - 2 me)/5 = (1 - 2 × 2)/5 = -3/5 

Y1 = x1 / 4 = (-3/5) / 4 = -3/20 

5- Prossiga de maneira semelhante para obter a segunda aproximação da solução do sistema de equações:

X2 = (1 - 2 y1)/5 = (1 - 2x (-3/20))/5 = 13/50 

Y2 = x2/4 = (13/50)/4 = 13/200

6- Terceira iteração:

X3 = (1 - 2 y2)/5 = (1 - 2 (13/200))/5 = 87/500

Y3 = x3/4 = (87/500)/4 = 87/2000

7- Quarta iteração, como a iteração final deste caso ilustrativo:

X4 = (1 - 2 y3)/5 = (1 - 2 (87/2000))/5 = 913/5000

Y4 = x4/4 = (913/5000)/4 = 913/20000

Esses valores coincidem muito bem com a solução encontrada através de outros métodos de resolução. O leitor pode verificar rapidamente com a ajuda de um programa matemático online.

Análise de método

Como pode ser visto, no método Gauss-Seidel, os valores aproximados obtidos para a variável anterior nessa mesma etapa devem ser substituídos na seguinte variável. Isso o diferencia de outros métodos iterativos, como Jacobi, nos quais cada etapa requer as abordagens para o estágio anterior. 

O método de Gauss-Seidel não é um procedimento paralelo, enquanto Gauss-Jordan é. É também a razão pela qual o método Gauss-Seidel tem um método mais rápido-sem convergência-o método da Jordânia.

Quanto à condição da matriz diagonalmente dominante, isso nem sempre é satisfeito. No entanto, na maioria dos casos, basta trocar as fileiras do sistema original para atender à condição. Além disso, o método quase sempre converge, mesmo quando a condição de dominância diagonal não é atendida.

O resultado anterior, obtido por quatro iterações do método Gauss-Seidel, pode ser escrito de uma maneira decimal:

Pode atendê -lo: quantos eixos de simetria um círculo tem?

X4 = 0,1826

Y4 = 0,04565

A solução exata para o sistema de equações levantadas é:

X = 2/11 = 0,1818

Y = 1/22 = 0,04545.

Então, apenas com 4 iterações, um resultado é obtido com um milésimo de precisão (0,001).

A Figura 1 ilustra como as iterações sucessivas convergem rapidamente para a solução exata.

Formulários

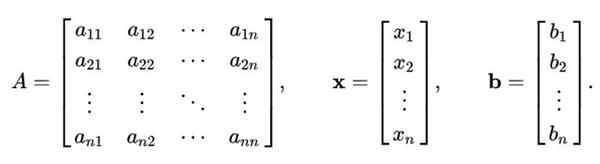
O método Gauss-Seidel não se limita apenas ao sistema de equações lineares 2 × 2. O procedimento acima pode ser generalizado para resolver um sistema linear de n equações com n desconhecidos, que é representado matrixly como este:

PARA X = b

Onde PARA É uma matriz n x n, enquanto X São os componentes do vetor N das variáveis ​​a serem calculadas; e b É um vetor que contém os valores de termos independentes.

Para generalizar a sequência de iterações aplicadas no caso ilustrativo a um sistema N x N, que deseja calcular a variável XI, A fórmula a seguir será aplicada:

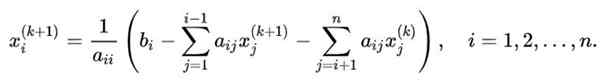
Nesta equação:

- k É o índice para o valor obtido na iteração k.

-K+1 Indica o novo valor no seguinte.

O número final de iterações é determinado quando o valor obtido na iteração K+1 difere do obtido imediatamente antes, em uma quantidade ε que é precisamente a precisão desejada.

Exemplos do método Gauss-Seidel

- Exemplo 1

Escreva um algoritmo geral que permita calcular o vetor de solução aproximada X de um sistema linear de equações nxn, dada a matriz do coeficiente PARA, O vetor de termos independentes b, O número de iterações (euter) e a inicial ou "semente" do vetor X.

Solução

O algoritmo consiste em dois ciclos "para", um para o número de iterações e outro para o número de variáveis. Seria o seguinte:

Para k ∊ [1 ... iter]

Para i ∊ [1… n]

X [i]: = (1/a [i, i])*(b [i] - ∑_{J = 1}ⁿ(A [i, j]*x [j]) + a [i, i]*x [i])

Pode atendê -lo: notação decimal

- Exemplo 2

Verifique a operação do algoritmo anterior aplicando -se ao software matemático Smath Studio GRATUITO E GRATUITO, disponível para Windows e Android. Tome como exemplo o caso da matriz 2 × 2 que nos serviu para ilustrar o método Gauss-Seidel.

Solução

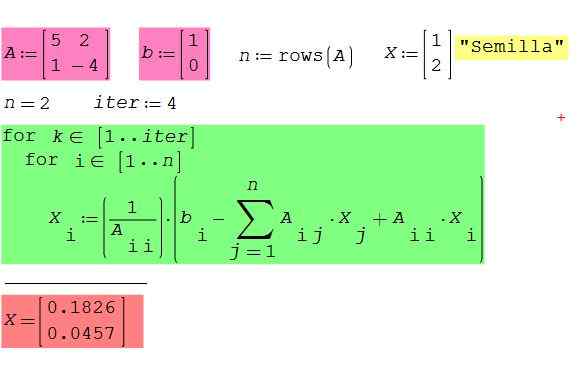Figura 2. Sistema de equações do Exemplo 2 x 2, usando software Smath Studio. Fonte: f. Zapata.

- Exemplo 3

Aplique o algoritmo Gauss-Seidel para o sistema de equações 3 × 3 a seguir, que foi ordenado anteriormente de tal maneira que os coeficientes diagonais sejam dominantes (isto é, de maior valor absoluto do que os valores absolutos dos coeficientes dos coeficientes da mesma linha):

9 x1 + 2 x2 - x3 = -2

7 x1 + 8 x2 + 5 x3 = 3

3 x1 + 4 x2 - 10 x3 = 6

Use o vetor nulo como semente e considere cinco iterações. Comente sobre o resultado.

Solução

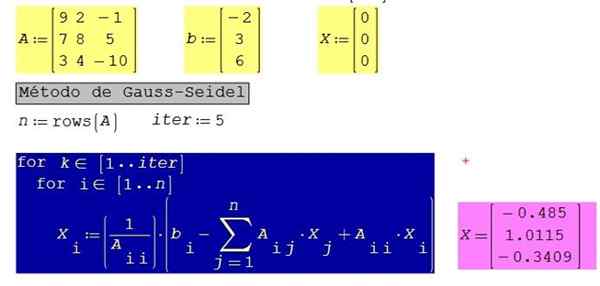Figura 3. Solução do sistema de equações do Exemplo 3 Resolvido, usando Smath Studio. Fonte: f. Zapata.

Para o mesmo sistema com 10 iterações em vez de 5, são obtidos os seguintes resultados: x1 = -0.485; X2 = 1.0123; X3 = -0.3406

Isso indica que é suficiente com cinco iterações para obter três decimais de precisão e que o método rapidamente transmite à solução.

- Exemplo 4

Por meio do algoritmo Gauss-Seidel, encontre a solução do sistema de equações 4 × 4 que ocorre abaixo:

10 x1 - x2 + 2 x3 + 0 x4 = 6

-1 x1 + 11 x2 - 1 x3 + 3 x4 = 25

2 x1 - 1 x2 + 10 x3 - 1 x4 = -11

0 x1 + 3 x2 - 1 x3 + 8 x4 = 15

Para iniciar o método, use esta semente:

x1 = 0, x2 = 0, x3 = 0 e x4 = 0

Considere 10 iterações e estime o erro do resultado, comparando com a iteração número 11.

Solução

Figura 4. Solução do sistema de equações do Exemplo 4 Resolvido, usando Smath Studio. Fonte: f. Zapata.

Ao comparar com a seguinte iteração (número 11), o resultado é idêntico. As maiores diferenças entre as duas iterações são da ordem de 2 × 10^-8, O que significa que a solução mostrada tem precisão de pelo menos sete decimais.

Referências

1. Métodos de solução iterativa. Gauss-seidel. Recuperado de: CIMAT.mx
2. Métodos numéricos. Gauss-seidel. Recuperado de: teste.Cua.Uam.mx
3. Numérico: Método Gauss-Seidel. Recuperado de: Aprenda em Linea.você.Edu.co
4. Wikipedia. Método Gauss-Seidel. Recuperado de: em. Wikipedia.com
5. Wikipedia. Método Gauss-Seidel. Recuperado de: é.Wikipedia.com